Россия, Щелково
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 07.04.2024 22:34
Фёдорова Ирина Юрьевна
учитель математике
53 года
1 402
36 394 
Местоположение
Специализация
Оценка достижений планируемых результатов обучения математике в условиях реализации ФГОС СОО
Категория:
Геометрия
04.10.2019 00:31
Просмотр содержимого документа
«Оценка достижений планируемых результатов обучения математике в условиях реализации ФГОС СОО»
Логико – математический анализ определения «Перпендикулярные плоскости»
УМК «Геометрия. 10-11 классы» авт. Л.С. Атанасян и др.
| Формулировка определения | Вид определения | Схема | Чертеж |
| Две пересекающиеся плоскости называются перпендикулярными (взаимно перпендикулярными), если угол между ними равен 90. | через род и видовые отличия | геометрическая фигура И две плоскости пересекаются, образуя четыре двугранных угла И линейный угол образованных двугранных углов равен 90 |
|
Логико – математический анализ признака «Перпендикулярности плоскостей»
| Формулировка теоремы | Вид теоремы | Метод доказательства | Доказательство |
| Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны. | условная | аксиоматический прямой | Д ; АВ; АВ; АВ=А. Доказать: . Доказательство: =АС, причем АВАС (по условию АВ); строим AD, так чтобы AD и АDАС, тогда BAD – линейный угол двугранного угла образованного при ; Т.к. АВ, то BAD=90, следовательно . |
ано:Утверждения:
прямое: «Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны» (истинно);
обратное: «Если плоскости перпендикулярны, то одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости» (истинно);
противоположное: «Если ни одна из двух плоскостей не проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости не перпендикулярны» (истинно);
обратное к противоположному: «Если плоскости не перпендикулярны, то ни одна из двух плоскостей не проходит через прямую, перпендикулярную к другой плоскости» (истинно).
Примеры предметных (метапредметных) результатов изучения темы «Перпендикулярные плоскости»
|
| Базовый уровень «Проблемно-функциональные результаты» | Углубленный уровень «Системно-теоретические результаты» | ||
| Раздел | I. Выпускник научится | III. Выпускник получит возможность научиться | II. Выпускник научится | IV. Выпускник получит возможность научиться |
| Требования к результатам | ||||
| Перпендикулярность плоскостей | Оперировать (отвечать на поставленный вопрос) на базовом уровне понятиями: прямая, плоскость в пространстве, перпендикулярность прямых и плоскостей; изображать (контроль в форме сличения способа действия и его результата с заданным эталоном) изучаемые фигуры от руки и с применением простых чертежных инструментов; извлекать (анализ) информацию о пространственных фигурах, представленную на чертежах и рисунках; применять (синтез) теорему Пифагора при вычислении расстояний между точками. В повседневной жизни и при изучении других предметов: соотносить (анализ) абстрактные геометрические понятия и факты с реальными жизненными объектами и ситуациями; использовать (синтез) свойства пространственных геометрических фигур для решения типовых задач практического содержания. | Оперировать (отображать предметное содержание в речи) понятиями: прямая, плоскость в пространстве, перпендикулярность прямых и плоскостей; применять (анализ и синтез) для решения задач геометрические факты, если условия применения заданы в явной форме; извлекать, интерпретировать и преобразовывать (анализ и синтез) информацию о геометрических фигурах, представленную на чертежах; описывать (отображать предметное содержание в речи) взаимное расположение прямых и плоскостей в пространстве; формулировать (отображать предметное содержание в речи) свойства и признаки фигур; доказывать (аргументировать) геометрические утверждения; вычислять (анализ, синтез) расстояния и углы в пространстве. В повседневной жизни и при изучении других предметов: использовать анализ, синтез) свойства геометрических фигур для решения задач практического характера и задач из других областей знаний. | Владеть (аргументировать) геометрическими понятиями при решении задач и проведении математических рассуждений; исследовать (анализ, синтез, причинно-следственные связи) чертежи, извлекать, интерпретировать и преобразовывать информацию, представленную на чертежах; выполнять (поиск) необходимые для решения задачи дополнительные построения, исследовать (анализ, сравнение, синтез) возможность применения теорем и формул для решения задач; уметь формулировать (отображать предметное содержание в речи) и доказывать (аргументировать) геометрические утверждения; уметь применять (анализ, синтез, причинно-следственные связи) перпендикулярности прямой и плоскости при решении задач; владеть (отображать предметное содержание в речи) понятиями ортогональное проектирование, наклонные и их проекции; владеть (отображать предметное содержание в речи) понятиями двугранный угол, угол между плоскостями, перпендикулярные плоскости и уметь применять их при решении задач; владеть (отображать предметное содержание в речи) понятием прямоугольный параллелепипед и применять его при решении задач. В повседневной жизни и при изучении других предметов: составлять с использованием свойств фигур математические модели для решения задач практического характера и задач из смежных дисциплин, исследовать полученные модели и интерпретировать (анализ, синтез, причинно-следственные связи) результат. | Иметь (контроль в форме сличения способа действия и его результата с заданным эталоном) представление об аксиоматическом методе; уметь применять (анализ, синтез, причинно-следственные связи) для решения задач свойства плоских и двугранных углов; иметь (контроль в форме сличения способа действия и его результата с заданным эталоном) представление о площади ортогональной проекции; иметь (контроль в форме сличения способа действия и его результата с заданным эталоном) представление о трехгранном и многогранном угле и применять (анализ, синтез, причинно-следственные связи) свойства плоских углов многогранного угла при решении задач; уметь решать (анализ, синтез, причинно-следственные связи) задачи на плоскости методами стереометрии. |
|
| ||||
ТИПОВАЯ УЧЕБНАЯ ЗАДАЧА №1 «ГЕОМЕТРИЧЕСКОЕ ПОНЯТИЕ»
Составить схему определения понятия «Перпендикулярные плоскости»
Задание: Прочитайте текст и дополните схему определения понятия «Перпендикулярные плоскости»
Две пересекающиеся плоскости называются перпендикулярными (взаимно перпендикулярными), если угол между ними равен 90.
| «Перпендикулярные плоскости» геометрическая фигура И две плоскости пересекаются, образуя четыре двугранных угла И линейный угол образованных двугранных углов равен 90 О |
бозначается: .Видоизменить формулировку определения «Перпендикулярные плоскости»
Задание: Укажите верные утверждения:
1) Если линейный угол двугранного угла прямой, то плоскости называются перпендикулярными (взаимно перпендикулярными).
2) Если линейный угол двугранного угла равен 90, то плоскости называются перпендикулярными (взаимно перпендикулярными).
3) Отметим на ребре двугранного угла точку и в каждой грани из этой точки проведем луч. Если угол образованный этими лучами прямой, то плоскости называются перпендикулярными (взаимно перпендикулярными).
4) Отметим на ребре двугранного угла точку и в каждой грани из этой точки проведем луч. Если угол образованный этими лучами равен 90, то плоскости называются перпендикулярными (взаимно перпендикулярными).
5) Отметим на ребре двугранного угла точку и в каждой грани из этой точки проведем луч перпендикулярно ребру. Если угол образованный этими лучами прямой, то плоскости называются перпендикулярными (взаимно перпендикулярными).
6) Отметим на ребре двугранного угла точку и в каждой грани из этой точки проведем луч перпендикулярно ребру. Если угол образованный этими лучами равен 90, то плоскости называются перпендикулярными (взаимно перпендикулярными).
7) Отметим на ребре двугранного угла точку и в каждой грани из этой точки проведем луч. Если эти лучи перпендикулярны ребру, то плоскости называются перпендикулярными (взаимно перпендикулярными).
ТИПОВАЯ УЧЕБНАЯ ЗАДАЧА №2 «НАБОР ОБЪЕКТОВ»
Исследовать наличие признаков понятия «Перпендикулярные плоскости» у данных объектов, выполнив их сравнение
Задание: Укажите рисунки, на которых изображены перпендикулярные плоскости.
| А)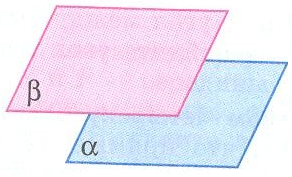
| Б)
| В)
| Г)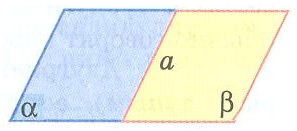
|
| Д)
| Е)
| Ж)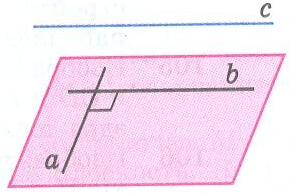
| З)
|
| К)
| Л)
| М)
| Н)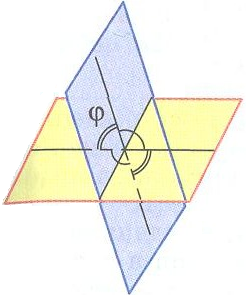
|
| О)
| П)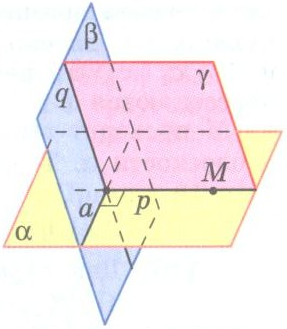
| Р)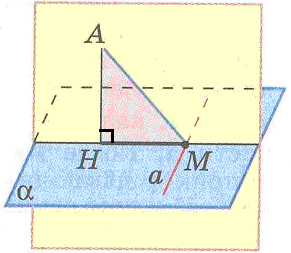
| С)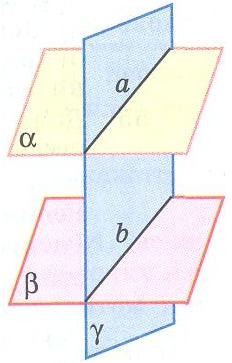
|
По аналогии составить набор объектов для подведения под понятие «Параллельные плоскости».
Задание: Составить набор объектов для подведение под понятие «Параллельные плоскости». Предложите соседу по карте выбрать среди рисунков те, где изображены параллельные плоскости.
ТИПОВАЯ УЧЕБНАЯ ЗАДАЧА №3 «СИСТЕМАТИЗАЦИЯ»
Составить классификационную схему взаимосвязи понятий «Расположение двух плоскостей в пространстве»
Задание:
1) Прочитайте текст аксиомы А3 и установите, о каких геометрических понятиях идет речь.
Если две различные плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих прямых. (В таком случае говорят, что плоскости пересекаются по прямой).
2) Выберите основание для разбиения по группам и выполните данное разбиение.
3) Выясните, есть ли основание для разбиения одной групп на подгруппы. Выполните разбиение.
| две различные плоскости | ||
| имеют общую точку | не имеют общую точку | |
| пересекаются | не пересекаются параллельные плоскости | |
| один из двугранных углов | ||
| не равен 90 | равен 90 | |
| | перпендикулярные плоскости | |
ТИПОВАЯ УЧЕБНАЯ ЗАДАЧА №4 «ТЕОРЕМА»
Выделять условие и заключение теоремы «Признак перпендикулярности плоскостей», интерпретировать их в знаках и символах.
Задание: Прочитайте формулировку теоремы и заполните пропуски.
Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны (см. чертеж).
Выполнять пошаговую запись доказательства теоремы «Признак перпендикулярности плоскостей», используя нужные аргументы
Задание: Прочитайте текст доказательства признака перпендикулярности в учебнике. В соответствии с текстом выполните пошаговую запись доказательства, заполнив пропуски, и нанесите недостающие обозначение на чертеже.
| Дано: ; АВ; АВ; АВ=А. Доказать: . Доказательство: =АС, причем АВАС (по условию АВ); с Т.к. АВ, то BAD=90, следовательно . |
Видоизменить формулировку теоремы «Признак перпендикулярности плоскостей» и устанавливать истинность полученных утверждений.
Задание: Выделите условие изученной теоремы и заключение. Сформулируйте обратное утверждение, противоположное, обратное противоположному. Являются ли сформулированные утверждения теоремами?
| условие теоремы «Признак перпендикулярности прямых» | одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости |
| заключение теоремы «Признак перпендикулярности прямых» | плоскости перпендикулярны |
Утверждения:
1) Обратное: «Если плоскости перпендикулярны, то одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости».
2) Противоположное: «Если ни одна из двух плоскостей не проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости не перпендикулярны».
3) Обратное противоположному: «Если плоскости не перпендикулярны, то ни одна из двух плоскостей не проходит через прямую, перпендикулярную к другой плоскости».
Логико – математический анализ задачи по теме «Перпендикулярные плоскости»
| Формулировка задачи | Вид | Метод | Решение: |
| Из точек P и Q, лежащих на двух взаимно перпендикулярных плоскостях, проведены перпендикуляры PH и QC на прямую пересечения плоскостей и . Найдите длину отрезка PQ, если PH = HC = 6 см и QC = 7 см. Дано: ; = с; P ; Q ; PH с; PH с; QC с; QC с; PH = 6 см, QC = 7 см, HC = 6 см. Найти: PQ.
| вычисление расстояния между точками | по структуре – прямой, синтетический; по использованию математического аппарата – алгебраический. | I способ: Так как ; = с; QC ; QC с, то QC (по свойству перпендикулярных плоскостей), отсюда QC CH. Значит QCH прямоугольный (по определению). Из прямоугольного QCH по теореме Пифагора находим квадрат гипотенузы: HQ2=QС2+HC2=72+62=49+36=85. Так как ; = с; PH ; PH с, то PH (по свойству перпендикулярных плоскостей), отсюда PH HQ. Значит PHQ прямоугольный (по определению). Из прямоугольного PHQ по теореме Пифагора находим гипотенузу: PQ2=PH2+HQ2=62+85=36+85=121, отсюда PQ = 11 см. II способ: Так как ; = с; PH ; PH с, то PH (по свойству перпендикулярных плоскостей), отсюда PH CH. Значит PCH прямоугольный (по определению). Из прямоугольного PCH по теореме Пифагора находим квадрат гипотенузы: РC2=РH2+HC2=62+62=36+36=72. Так как ; = с; QC ; QC с, то QC (по свойству перпендикулярных плоскостей), отсюда QC РС. Значит РСQ прямоугольный (по определению). Из прямоугольного РСQ по теореме Пифагора находим гипотенузу: PQ2=PС2+QС2=72+72=72+49=121, отсюда PQ = 11 см. Ответ: PQ = 11 см. |
| Опорная задача: Из точки, лежащей на одной из взаимно перпендикулярных плоскостях, проведен перпендикуляр на прямую пересечения плоскостей. Найти длину наклонной, проведенную из этой точки на другую плоскость. | |||
| Аналогичная задача: Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений. (УМК Атанасян Л.С. и др.; № 187) Используется в заданиях ЕГЭ, например, прототип задания 8 (№ 245370, № 284363 и аналогичные) | |||
| Взаимно обратная задача: Из точек P и Q, лежащих на двух взаимно перпендикулярных плоскостях, проведены перпендикуляры PH и QC на прямую пересечения плоскостей и . Найдите длины отрезков PH, QC и HC, если PH = HC, QC PH на 1 см и PQ = 11 см. | |||
ТИПОВАЯ УЧЕБНАЯ ЗАДАЧА №5 «МАТЕМАТИЧЕСКАЯ ЗАДАЧА»
Выделять условие и требование геометрической задачи, интерпретировать их в знаках и символах
Задание: Прочтите геометрическую задачу. Выполните чертеж и запишите условие и требование.
Из точек P и Q, лежащих на двух взаимно перпендикулярных плоскостях, проведены перпендикуляры PH и QC на прямую пересечения плоскостей и . Найдите длину отрезка PQ, если PH = 6 см, QC = 7 см, HC = 6 см.
| Дано: ; = с; P ; Q ; PH с; PH с; QC с; QC с; PH = 6 см, QC = 7 см, HC = 6 см. Найти: PQ. | |
Выводить следствия из условия задачи при поиске её решения
Задание: Выведите следствия из условия, используя свойство перпендикулярных плоскостей. Составьте план решения задачи.
| Свойство перпендикулярных плоскостей: Если две плоскости взаимно перпендикулярны, то любая прямая, лежащая в одной из них и перпендикулярная линии их пересечения, перпендикулярна второй плоскости. |
| 1) Так как ; = с; PH ; PH с, то PH , отсюда PH HQ. Значит PHQ прямоугольный: PH = 6 см – катет, HQ – катет, PQ – гипотенуза (искомый отрезок). 2) Так как ; = с; QC ; QC с, то QC , отсюда QC CH. Значит QCH прямоугольный: QC = 7 см – катет, HC = 6 см – катет, HQ – гипотенуза, которая является неизвестным катетом для PHQ. |
| План решения задачи: 1) Из прямоугольного QCH по теореме Пифагора находим гипотенузу HQ. 2) Из прямоугольного PHQ по теореме Пифагора находим гипотенузу PQ (искомый отрезок). |
Выполнять пошаговую запись решения задачи, реализуя план и используя нужные математические аргументы.
Задание: Запишите решение задачи, используя структуру:
1) Так как ; = с; QC ; QC с, то QC (по свойству перпендикулярных плоскостей), отсюда QC CH. Значит QCH прямоугольный (по определению).
2) Из прямоугольного QCH по теореме Пифагора находим квадрат гипотенузы: HQ2=QC2+HC2=72+62=49+36=85.
3) Так как ; = с; PH ; PH с, то PH (по свойству перпендикулярных плоскостей), отсюда PH HQ. Значит PHQ прямоугольный (по определению).
4) Из прямоугольного PHQ по теореме Пифагора находим гипотенузу: PQ2=PH2+HQ2=62+85=36+85=121, отсюда PQ = 11 см.
Ответ: PQ = 11 см.
ТИПОВАЯ УЧЕБНАЯ ЗАДАЧА №6 «ПРИКЛАДНАЯ ЗАДАЧА»
Использовать метод математического моделирования для решения практико-ориентированных задач.
Задание: Прочтите задачу. Постройте математическую модель этой задачи.
Каким образом следует использовать обратную теорему Пифагора для того, чтобы проверить, перпендикулярны ли друг другу соседние стены помещения (кабинета математики)?
М атематическая модель задачи: Пусть стены помещения – плоскости и , пол – плоскость , причем =a, =b, =c. Предположим, что стены помещения вертикальные, а пол горизонтальный, иначе говоря, и , отсюда b (так как плоскость, перпендикулярная двум пересекающимся плоскостям, перпендикулярна линии их пересечения). Значит, ba и bc (по определению прямой перпендикулярной плоскости). Таким образом, (ac) – линейный угол двугранного угла (по определению), образованного стенами помещения, градусную меру которого нам и предстоит определить по обратной теореме Пифагора, используя пифагорейскую тройку.
Задание: Сформулируйте геометрическую задачу в математических терминах и решите её.
В ыполните необходимые измерения и определите перпендикулярность плоскостей и .
Решение: Пусть abc=A. Отложим на полупрямых a и c отрезки AB и AC длиной 3 дм и 4 дм соответственно. BAC = 90 тогда и только тогда, когда BC = 5 дм.
В повседневной жизни использовать свойства геометрических фигур
для решения задач практического характера.
Домашнее задание: В домашних условия проверить, перпендикулярны ли друг другу стены комнат квартиры обучающегося. Оформить задание как отчет по решению исследовательской практико – ориентированной задачи.
Примечание: При построении математической модели делается предположение о вертикальности стен и горизонтальности пола помещения. Проверка этого предположения так же является практико – ориентированными задачами:
| Формулировка задания | Указания для решения | Проверяемая теории |
| Как проверить вертикальное расположение стены с помощью подручных средств в домашних условиях? | Вертикальное расположение стен проверяют при помощи отвеса (шнур с грузиком). | Признак перпендикулярности плоскостей. |
| Как проверить горизонтальное расположение пола с помощью подручных средств в домашних условиях? | Горизонтальное расположение пола проверяют с помощью уровня (емкость с водой). | Свойство параллельных плоскостей. |
ТИПОВАЯ УЧЕБНАЯ ЗАДАЧА №7 «МАТЕМАТИЧЕСКИЙ ТЕКСТ»
Отвечать на вопросы к прочитанному тексту
Задание: Прочитайте математический текст. Ответьте на данные вопросы к прочитанному тексту.
«§ 6.3. Ортогональное проецирование
Параллельное проецирование, направление которого перпендикулярно плоскости проекции, называется ортогональным проецированием. Проекция фигуры, образующаяся при ортогональном проецировании, называется ортогональной проекцией, или просто проекцией этой фигуры.
Поскольку ортогональное проецирование является особым видом параллельного проецирования, то для него выполняются все свойства последнего. Ортогональной проекцией прямой a, не перпендикулярной плоскости проекции, является некоторая прямая a (рис. 6.39), а прямой a, параллельной плоскости проекции , - прямая a, параллельная прямой a (рис. 6.40).
Отметим, что прямые, перпендикулярные одной из параллельных плоскостей, перпендикулярны и остальным, поэтому ортогональное проецирование на одну из таких плоскостей будет ортогональным и на остальные плоскости. Очевидно, что ортогональные проекции фигуры на параллельные плоскости равны между собой.
Ортогональное проецирование также имеет только ему присущие свойства. Одно из них выражает теорема о площади ортогональной проекции многоугольника.
Теорема о площади ортогональной проекции многоугольника
Площадь ортогональной проекции произвольного многоугольника на плоскость равна произведению площади самого многоугольника на косинус угла между плоскостью многоугольника и плоскостью проекции.»
Вопросы для самоконтроля:
1) Может ли ортогональная проекция отрезка быть равной длине этого отрезка?
2) Может ли ортогональная проекция отрезка быть больше (меньше) длины отрезка?
3) Могут ли ортогональные проекции прямых совпадать?
4) Может ли ортогональная проекция куба быть квадратом?
5) Как построить ортогональную проекцию геометрической фигуры?
6) Какова связь между площадью многоугольника и площадью его ортогональной проекции?
7) Может ли площадь ортогональной проекции многоугольника быть равной площади этого многоугольника?
8) Может ли площадь ортогональной проекции многоугольника быть больше (меньше) площади этого многоугольника?
9) Ортогональное проецирование на плоскость задается прямой проецирования, образующей с плоскость проекции угол . Укажите величину угла .
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
Полезное для учителя
Реализация образовательных программ осуществляется с применением исключительно электронного обучения и ДОТ
