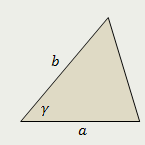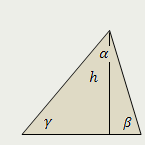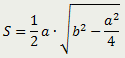Памятка-формулы площадей фигур для подготовки к ОГЭ по математике

Конфигурация

Название фигуры

Формула

Правило

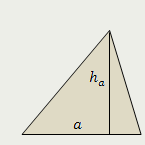
Треугольник

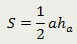
Площадь треугольника равна половине произведения его стороны на высоту, проведённую к этой стороне

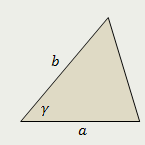
Треугольник

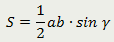
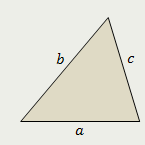
Площадь треугольника равна половине произведения двух его сторон на синус угла между ними

Треугольник

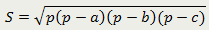
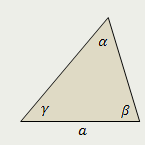
Площадь треугольника равна корню квадратному из произведения полупериметра этого треугольника и разностей полупериметра и всех его сторон

Треугольник

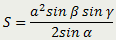
Площадь треугольника равна отношению произведения квадрата его стороны на синусы прилежащих углов к удвоенному синусу противолежащего угла

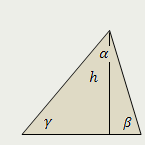
Треугольник

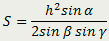
Площадь треугольника равна отношению произведения квадрата его высоты на синус угла, из вершины которого проведена эта высота, к удвоенному произведению синусов двух других углов

Треугольник

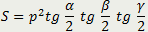
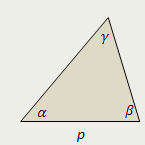
Площадь треугольника равна произведению квадрата его полупериметра на тангенсы половин всех углов треугольника

Прямоугольный треугольник

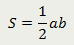
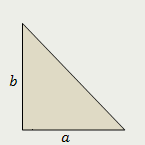
Площадь прямоугольного треугольника равна половине произведения его катетов

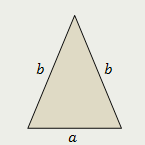
Равнобедренный треугольник

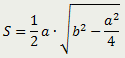
Площадь равнобедренного треугольника равна половине произведения его основания на корень квадратный из разности квадратов боковой стороны и половины основания 

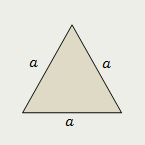
Равносторонний треугольник

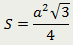
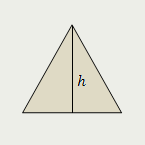
Площадь равностороннего треугольника равна четверти произведения квадрата стороны этого треугольника и квадратного корня из трёх

Равносторонний треугольник

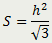
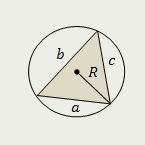
Площадь равностороннего треугольника равна отношению квадрата его высоты к квадратному корню из трёх

Треугольник

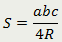
Площадь треугольника равна отношению произведения всех его сторон к четырём радиусам, описанной около него окружности

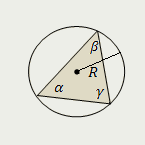
Треугольник

Площадь треугольника равна удвоенному произведению квадрата радиуса, описанной около него окружности, и синусов всех его углов

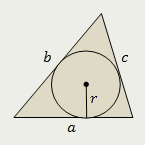
Треугольник

Площадь треугольника (многоугольника) равна произведению его полупериметра и радиуса окружности, вписанной в этот треугольник (многоугольник)

Треугольник

Площадь треугольника равна произведению квадрата радиуса вписанной окружности на котангенсы половин всех углов треугольника

Прямоугольник

Площадь прямоугольника равна произведению двух соседних его сторон

Квадрат

Площадь квадрата равна квадрату его стороны

Квадрат

Площадь квадрата равна половине квадрата его диагонали

Параллелограмм

Площадь параллелограмма равна произведению его стороны на высоту, проведённую к этой стороне

Параллелограмм

Площадь параллелограмма равна произведению двух соседних его сторон на синус угла между ними

Ромб

Площадь ромба равна произведению квадрата его стороны на синус одного из его углов 

Ромб (дельтоид)

Площадь ромба (как и дельтоида) равна половине произведения его диагоналей

Трапеция

Площадь трапеции равна произведению полусуммы её оснований на высоту

Трапеция

Площадь трапеции равна произведению её средней линии на высоту

Выпуклый четырёхугольник

Площадь выпуклого четырёхугольника равна половине произведения его диагоналей на синус угла между ними

Вписанный четырёхугольник

Площадь четырёхугольника, вписанного в окружность, равна корню квадратному из произведения разностей полупериметра этого четырёхугольника и всех его сторон

Круг

Площадь круга равна произведению числа "пи" на квадрат радиуса

Круг

Площадь круга равна четверти произведения числа "пи" на квадрат диаметра

Круговой сектор

формулы для случаев градусной и радианной мер центральных углов

Площадь кругового сектора равна произведению площади единичного сектора (сектор, соответствующий центральному углу с мерой равной единице) на меру центрального угла, соответствующего данному сектору

Круговое кольцо

Площадь кругового кольца равна произведению числа "пи" на разность квадратов внешнего и внутреннего радиусов 

Круговое кольцо

Площадь кругового кольца равна четверти произведения числа "пи" на разность квадратов внешнего и внутреннего диаметров

Круговое кольцо

Площадь кругового кольца равна удвоенному произведению числа "пи", среднего радиуса кольца и его ширины