| З адачи на кратное сравнение чисел. адачи на кратное сравнение чисел.
Чтобы узнать, во сколько раз одно число больше или меньше другого, надо большее число разделить на меньшее. 8:2=4 (раза) 8 больше, чем 2 в 4 раза 2 меньше, чем 8 в 4 раза Порядок действий.
В выражениях без скобок сначала выполняется умножение и деление, а затем сложение и вычитание. Умножение и деление, а также сложение и вычитание между собой выполняются по порядку, так как это действия одной ступени: 94 - 2 .2 + 3 – 25 : 5 = 94 – 4 + 3 – 5 = 88
В выражениях со скобками сначала выполняются все действия в скобках, затем действия умножения и деления и только после этого остальные действия по порядку: 22 - (15 + 3) : 6 + 7 . (11- 7) + 5 = 22 – 18 : 3 + 7 . 3 + 25 = 22 – 6 + 21 + 5 = 42
Если в выражениях одни скобки находятся внутри других, сначала выполняют действия во внутренних скобках.
Периметр
Периметр геометрической фигуры – это сумма длин всех сторон фигуры. Единицы периметра: мм, см, дм, м  I способ: (4 + 3) . 2 = 7 . 2 = 14 см (Сложить длину и ширину прямоугольника и взять эту сумму 2 раза) II способ: 4 . 2 + 3 . 2 = 8 + 6 = 14 см (Длину взять 2 раза, ширину взять 2 раза, полученные суммы сложить.) | П ериметр квадрата ериметр квадрата  
У квадрата длина равна ширине: 3см + 3 см + 3 см + 3 см = 3 см х 4 = 12 см Найти периметр квадрата, значит, его длину умножить на 4. 3 . 4=12 см
Единицы площади: мм2, см 2, дм 2, м 2 1 см2 - это квадрат, длина стороны которого равна 1 см. 1 дм2 – это квадрат, длина стороны которого равна 1 дм. 1 м2 – это квадрат, длина стороны которого равна 1 м.
Площадь прямоугольника.
Чтобы найти площадь прямоугольника, надо его длину умножить на ширину или наоборот. 4 . 3 = 3 . 4 = 12 см 2 

Площадь квадрата. 
3 . 3 = 9 см 2
1 м2 = 100 дм2 = 10000 см2 1дм2 = 100 см2 = 10000 мм2 1см2 = 100 мм2 
|
| 
Запомни!
| на 2 больше | надо + 2 | | на 2 меньше | надо – 2 | | в 2 раза больше | надо . на 2 | | в 2 раза меньше | надо : на 2 |
Единицы массы
| 1 т = 10 ц = 1000 кг | 1 ц = 100 кг | 1 кг = 1000 г |
Деление с остатком: 28:3. Надо 28 разделить на 3. Самое большое число, которое делится на 3 без остатка и близкое к 28 – это 27. Делим 27 на 3, получаем 9. Мы разделили 27 на 3, а надо разделить 28. Узнаем, сколько единиц не разделили. Для этого из 28 вычтем 27, получится 1. Значит, 28 : 3=9 (ост.1). Делаем проверку: 9 . 3 + 1=28. Остаток должен быть меньше делителя. Остаток 1 меньше делителя 3. 28 : 3 = 9 (ост.1)
Окружность – линия, которая является границей круга. Центр окружности – точка, вокруг которой чертят окружность. 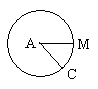 Отрезки АМ и АС – радиусы окружности. Если вершиной угла является центр окружности, угол называется центральным углом. Угол МАС или САМ– центральный угол. Сторонами центрального угла являются радиусы окружности. Радиусы одной окружности равны между собой: АМ = АС. Градус – мерка для измерения углов. Угол величиной в один градус записывают так: 10. Если угол разделить на 360 равных углов, то получится угол в 1 градус. Транспортир – прибор для измерения углов. | Распределительное свойство умножения относительно сложения: при умножении суммы на число значение выражения не изменится, если умножить на него каждое слагаемое и полученные результаты сложить.
Умножение суммы на число: (4+3) . 2.
(4 + 3) . 2 = 7 . 2 = 14 (4 + 3) . 2 = 4 . 2 + 3 . 2 = 8 + 6 = 14 Пользуясь этими способами умножения суммы на число, находим значения следующих выражений:
23 . 2 = (20 + 3) . 2 = 20 . 2 + 3 . 2 = 40 + 6 = 46 17 . 3 = (10 + 7) . 3 = 10 . 3 + 7 . 3 = 30 + 21 = 51
Умножение числа на сумму: 7 . (6 + 2).
7 . (6 + 2) = 7 . 8 = 56 7 . (6 + 2) = 7 . 6 + 7 . 2 = 42 + 14 = 56 Пользуясь этими способами умножения числа на сумму, находим значения следующих выражений:
4 . 15 = 4 . (10 + 5) = 4 . 10 + 4 . 5 = 40 + 20 = 60 3 . 28 = 3 . (20 + 8) = 3 . 20 + 3 . 8 = 60 + 24 = 84
Деление суммы на число: (6+4) : 2.
(6 + 4) : 2 = 10 : 2 = 5 (6 + 4) : 2 = 6 : 2 + 4 : 2 = 3 + 2 = 5
При делении суммы на число значение выражения не изменится, если разделить на него каждое слагаемое и полученные результаты сложить. Пользуясь этими способами деления суммы на число, находим значения следующих выражений:
28 : 2 = (20 + 8) : 2 = 20 : 2 + 8 : 2 = 10 + 4 = 14 3 6 : 2 = (20 + 16) : 2 = 20 : 2 + 16 : 2 = 10 + 8 = 18 6 : 2 = (20 + 16) : 2 = 20 : 2 + 16 : 2 = 10 + 8 = 18
Чтобы найти общие решения двух неравенств их объединяют фигурной скобкой и называют системой неравенств. |
|  система неравенств а a 17 Можно записать одно сложное (двойное) неравенство: 17 a
Единицы длины | 1 км = 1000 м 1 м = 10 дм = 100 см | 1 дм = 10 см = 100 мм 1см = 10 мм |
Единица вместимости – литр (л) Масса 1 л воды равна 1 кг
Единицы времени | 1 сут. = 24 ч 1 ч = 60 мин = 3600 с 1 мин = 60 с 1 неделя = 7 дней | 1 месяц = 28 (29), 30, 31 день 1 год = 365 (366) дней 1 век = 100 лет | Цена. Количество. Стоимость. Цена = стоимость : на количество (ц = с : к) Количество = стоимость : на цену (к = с : ц) Стоимость = цену . на количество (с = ц . к)
Скорость. Время. Расстояние. Расстояние = скорость . на время (s = v . t) Время = расстояние : на скорость (t = s : v) Скорость = расстояние : на время (v = s : t)
Единицы измерения расстояния: км, м Единицы измерения времени: ч, мин, с Единицы измерения скорости: км/ч, м/мин, м/с, км/ч 2м/с – читаем как 2 метра в секунду.
Числовой луч – наглядное изменение расположения чисел относительно друг друга. Он напоминает линейку с одинаковыми мерками. 
| 
Мерку, которую выбирают для построения числового луча, называют единичным отрезком. Координата – число, которое соответствует точке числового луча. Координату точки на числовом луче записывают так: М (3, Е (6), У (5)… Числовой луч чаще называют координатным лучом.
Дробные числа
Вместо слова половина часто говорят одна вторая. Одна вторая – это дробное число или дробь: ½. Знаменатель – (число под чертой) показывает, на сколько частей разделили. Числитель – (число над чертой) показывает, сколько таких частей взяли. Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше. Масштаб
Если истинные размеры изменены, то изображение выполнено в масштабе. 1:3 –в масштабе один к трём (размеры уменьшены в 3 раза).
Класс единиц и класс тысяч
10 сотен образуют новую единицу счёта – тысячу: 1000 Класс единиц – единицы (единицы 1 разряда), десятки (единицы второго разряда), сотни (единицы третьего разряда). Класс тысяч – тысячи (единицы четвёртого разряда), десятки тысяч (единицы пятого разряда), сотни тысяч (единицы шестого разряда).
Римские числа
| I – 1 II – 2 III – 3 IV – 4 | V – 5 VI – 6 VII –7 VIII – 8 IX – 9 | X – 10 L – 50 C – 100 D – 500 – 500 М – 1000 | Чётные числа – это числа, которые делятся на 2 без остатка. |






 адачи на кратное сравнение чисел.
адачи на кратное сравнение чисел.
 ериметр квадрата
ериметр квадрата



 6 : 2 = (20 + 16) : 2 = 20 : 2 + 16 : 2 = 10 + 8 = 18
6 : 2 = (20 + 16) : 2 = 20 : 2 + 16 : 2 = 10 + 8 = 18

 – 500
– 500 









