Параллельность прямых и плоскостей в пространстве.Геометрия.10 класс.

ГЕОМЕТРИЯ 10 класс

Тема: «Параллельность прямых и плоскостей в пространстве»

Параллельные прямые в пространстве

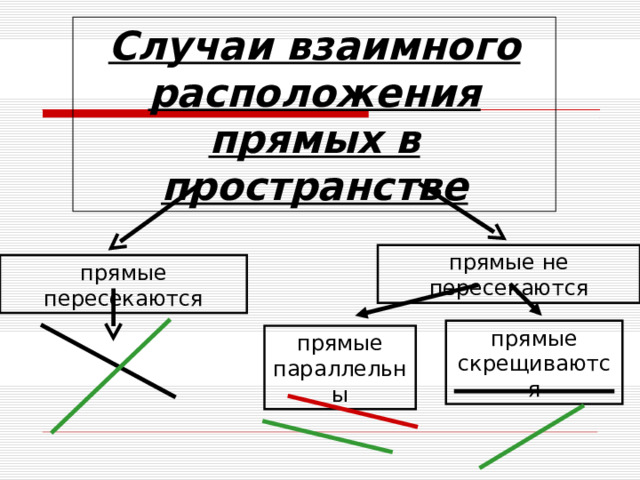
Случаи взаимного расположения прямых в пространстве

прямые не пересекаются

прямые пересекаются

прямые скрещиваются

прямые параллельны

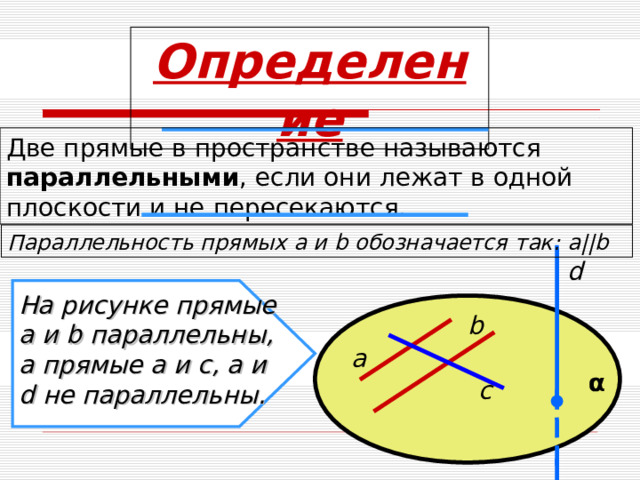
Определение

Две прямые в пространстве называются параллельными , если они лежат в одной плоскости и не пересекаются.

Параллельность прямых a и b обозначается так: a || b

d

На рисунке прямые

a и b параллельны,

а прямые a и c , a и d не параллельны.

b

a

α

c

4

Признак параллельных прямых

Если две прямые параллельны третьей, то они параллельны.

с

b

a

α

5

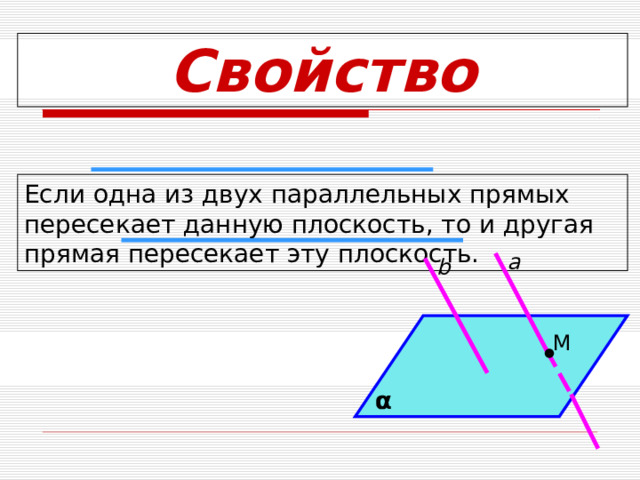
Свойство

Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.

a

b

M

α

6

Параллельность прямой и плоскости в пространстве

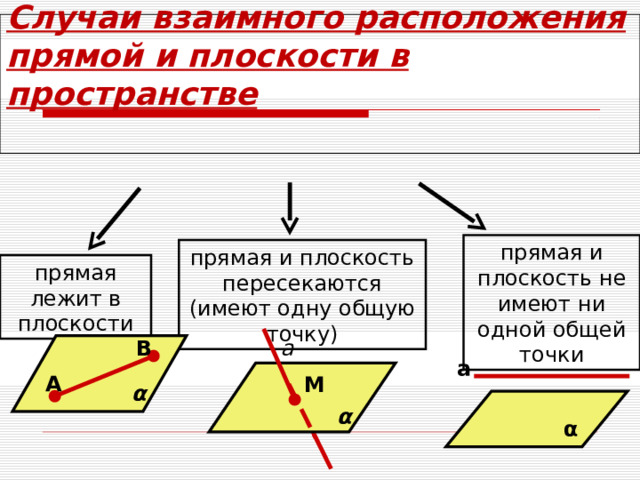
Случаи взаимного расположения прямой и плоскости в пространстве

прямая и плоскость не имеют ни одной общей точки

прямая и плоскость пересекаются (имеют одну общую точку)

прямая лежит в плоскости

В

а

а

А

М

α

α

α

8

Определение

Прямая и плоскость называются параллельными , если они не имеют общих точек.

8

Признак параллельности прямой и плоскости

• Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости

Свойства параллельных прямой и плоскости

Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости.

Если в одной из пересекающихся плоскостей лежит прямая, параллельная другой плоскости, то она параллельна линии пересечения плоскостей. 

Параллельность плоскостей

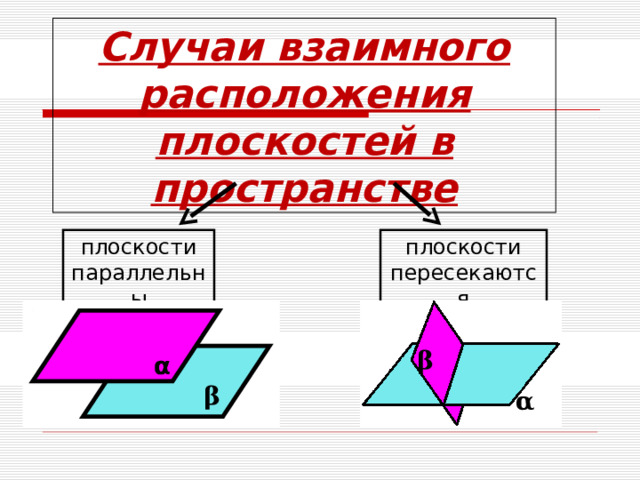
Случаи взаимного расположения плоскостей в пространстве

плоскости параллельны

плоскости пересекаются

β

α

β

α

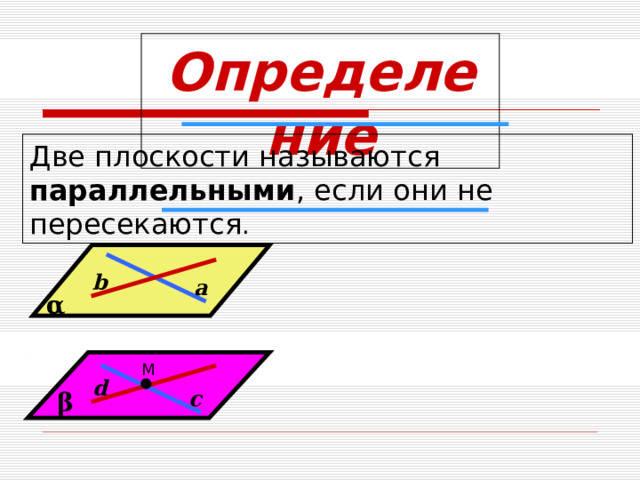
Определение

Две плоскости называются параллельными , если они не пересекаются .

b

a

α

M

d

c

β

14

Признак параллельности плоскостей

• Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.

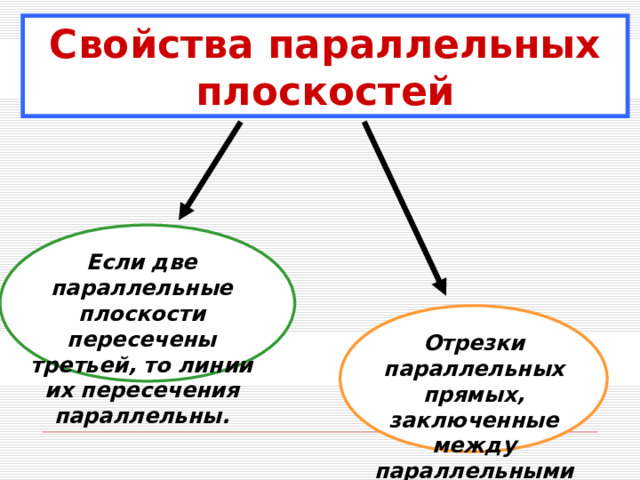
Свойства параллельных плоскостей

Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.

Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.

16

Решение задач

ТЕСТ

1. Верно ли утверждение: если две прямые не имеют общих точек, то они параллельны?

2. Точка М не лежит на прямой а.

а) Сколько прямых, не пересекающих прямую а, проходит через точку М?

б) Сколько из этих прямых параллельны прямой а?

3. Прямые а и с параллельны, а прямые а и b пересекаются.

а) Могут ли прямые b и с пересекаться?

б) Могут ли прямые b и с быть параллельны?

4. Прямая а параллельна плоскости α . Верно ли, что эта прямая не пересекает ни одну прямую, лежащую в плоскости α ?

5. Прямая а параллельна плоскости α .

а) Сколько прямых, лежащих в плоскости α , параллельны прямой а?

б) Параллельны ли друг другу эти прямые, лежащие в плоскости α ?

6. Могут ли быть равны два непараллельных отрезка, заключенные между параллельными плоскостями?

7. Две стороны параллелограмма параллельны плоскости α . Параллельны ли плоскость α и плоскость параллелограмма?

Задачи для самостоятельного решения

А

D

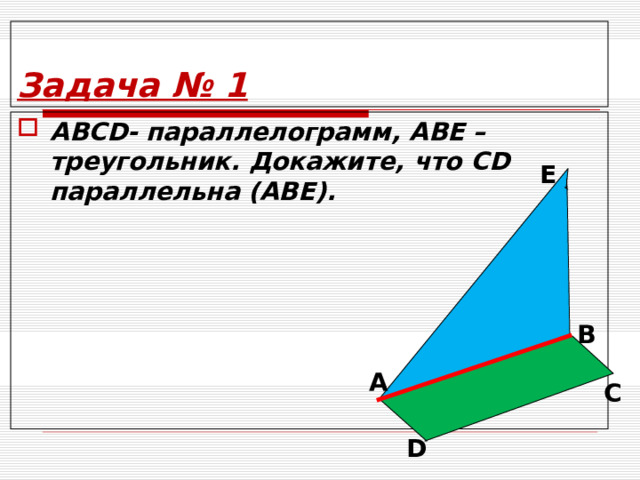
Задача № 1

• АВС D - параллелограмм, АВЕ – треугольник. Докажите, что CD параллельна (АВЕ).

Е

В

С

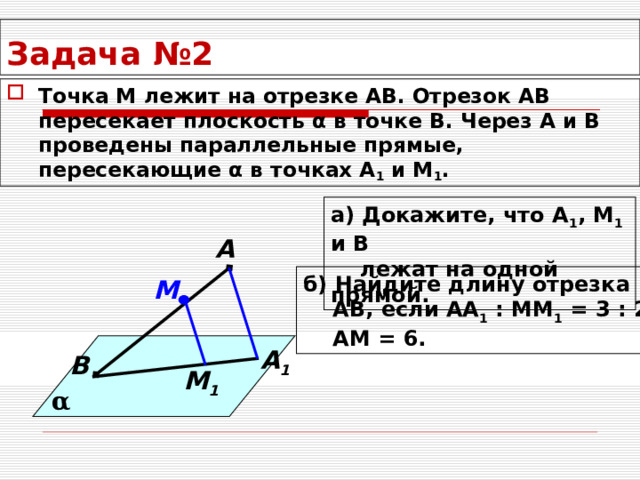
Задача №2

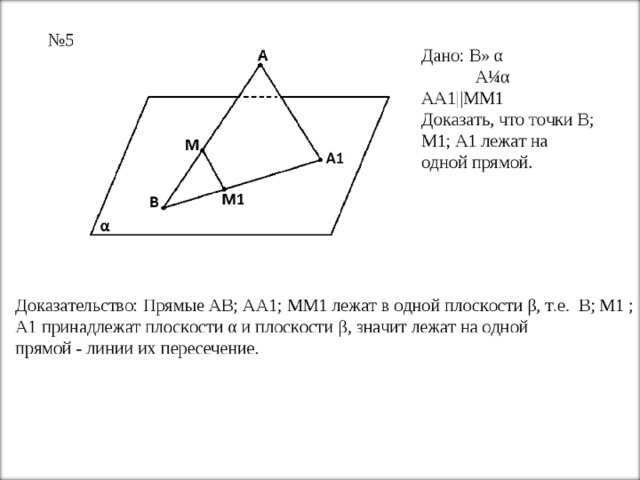
• Точка М лежит на отрезке АВ. Отрезок АВ пересекает плоскость α в точке В. Через А и В проведены параллельные прямые, пересекающие α в точках А 1 и М 1 .

а) Докажите, что А 1 , М 1 и В

лежат на одной прямой.

А

б) Найдите длину отрезка

АВ, если АА 1 : ММ 1 = 3 : 2,

АМ = 6.

М

А 1

В

М 1

α

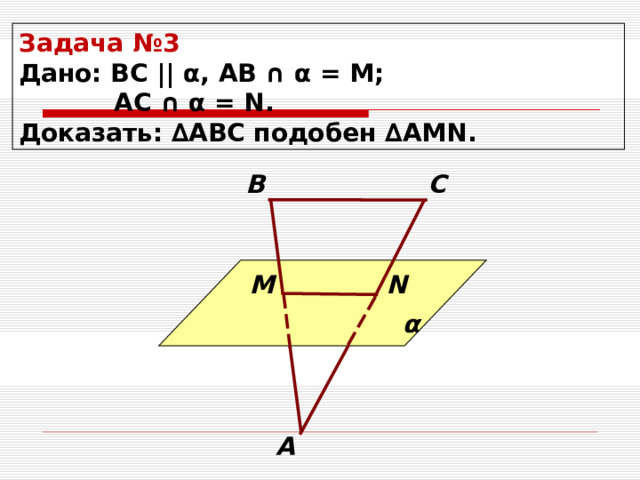
Задача №3

Дано: ВС || α , АВ ∩ α = М;

АС ∩ α = N .

Доказать: ∆АВС подобен ∆АМ N .

В

С

α

М

N

А

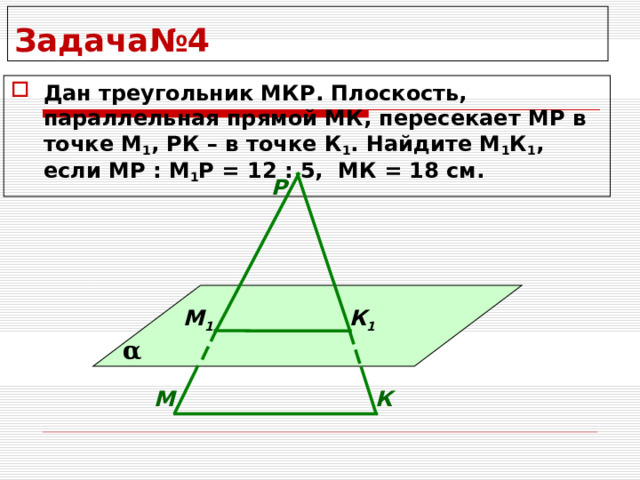
Задача№4

• Дан треугольник МКР. Плоскость, параллельная прямой МК, пересекает МР в точке М 1 , РК – в точке К 1 . Найдите М 1 К 1 , если МР : М 1 Р = 12 : 5, МК = 18 см.

Р

М 1

К 1

α

М

К