Россия, Таганрог
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 11.05.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 29.04.2025 09:48
Донченко Виктория Геннадиевна
учитель информатики
40 лет
4 819
10 970 
Местоположение
Специализация
Перевод чисел из одной системы счисления в другую.
Категория:
Информатика
12.02.2025 09:44
Просмотр содержимого документа
«Перевод чисел из одной системы счисления в другую.»
ПЕРЕВОД ЧИСЕЛ ИЗ ОДНОЙ ПОЗИЦИОННОЙ СИСТЕМЫ В ДРУГУЮ
ПРЕДСТАВЛЕНИЕ ИНФОРМАЦИИ В КОМПЬЮТЕРЕ
Ключевые слова
- система счисления
- триада
- тетрада
- «компьютерные» системы счисления
- «быстрый» перевод
Перевод целого десятичного числа в систему счисления с оcнованием q
Для перевода целого десятичного числа в систему счисления с основанием q следует:
- последовательно выполнять деление данного числа и получаемых целых частных на основание новой системы счисления до тех пор, пока не получится частное, равное нулю;
- полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие алфавиту новой системы счисления;
- составить число в новой системе счисления, записывая его, начиная с последнего остатка.
Реши сам
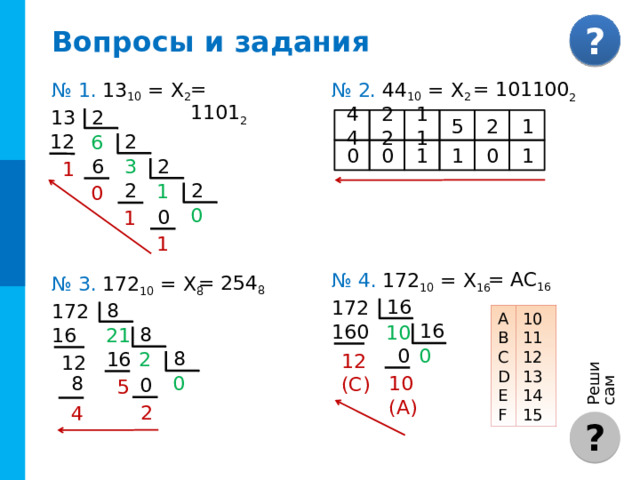
Вопросы и задания
= 101100 2
= 1101 2
№ 2. 44 10 = Х 2
№ 1. 13 10 = Х 2
2
13
22
44
11
5
2
1
2
12
6
1
1
0
0
1
0
2
3
6
1
2
2
1
0
0
0
1
1
= АС 16
№ 4. 172 10 = Х 16
= 254 8
№ 3. 172 10 = Х 8
16
172
8
172
Комментарии
Кнопка «?» переводит на скрытый слайд с дополнительными заданиями на закрепление навыков перевода.
Переход осуществляется на усмотрение учителя.
10
A
11
B
12
C
13
D
14
E
F
15
16
160
10
8
16
21
0
0
8
16
2
12 (С)
12
8
0
10 (А)
0
5
2
4
?
4
Решите самостоятельно
№ 5. Переведите десятичные числа в указанные системы счисления.
= 1100100 2
= 11101001 2
е) 233 10 = X 2
а) 100 10 = X 2
б) 187 10 = X 8
= 273 8
= 456 8
ж) 302 10 = X 8
в) 2572 10 = X 16
з) 3802 10 = X 16
= A0C 16
= EDA 16
= 12300 5
и) 950 10 = X 5
г) 1458 10 = X 5
= 21313 5
к) 41 10 = X 3
= 1222 3
д) 53 10 = X 3
= 1112 3
Комментарии
Количество и номера решаемых примеров на усмотрение учителя.
Задачи могут решаться самостоятельно или при фронтальной работе. Также можно организовать работу по вариантам.
Для удобства есть кнопка «Ответы», по которой выводятся ответы на все примеры сразу (без решения)
ОТВЕТ
4
Реши сам
Перевод целого десятичного числа в двоичную систему счисления
Для перевода числа Х (X≤10000) в двоичную систему счисле-ния можно воспользоваться таблицей степеней двойки.
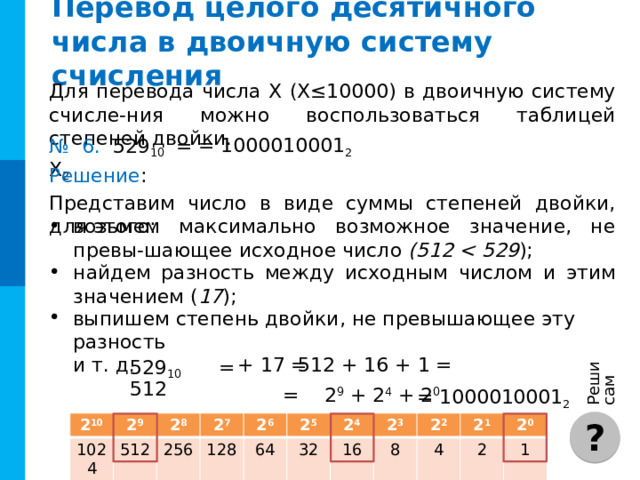
= 1000010001 2
№ 6. 529 10 = Х 2
Решение :
Представим число в виде суммы степеней двойки, для этого:
Решение :
Представим число в виде суммы степеней двойки:
- когда исходное число представлено в виде суммы, строим его двоичное представление, записав 1 в разрядах, соответствующих слагаемым, вошедшим в сумму, и 0 — во всех остальных разрядах.
- возьмем максимально возможное значение, не превы-шающее исходное число (512 );
- найдем разность между исходным числом и этим значением ( 17 );
- выпишем степень двойки, не превышающее эту разность и т. д.
+ 17 =
512 + 16 + 1 =
529 10 = 512
= 1000010001 2
= 2 9 + 2 4 + 2 0
?
2 10
2 9
1024
2 8
512
256
2 7
2 6
128
64
2 5
32
2 4
2 3
16
8
2 2
4
2 1
2
2 0
1
Решите самостоятельно
№ 7. Переведите десятичные числа в двоичную систему счисления, используя таблицу степеней двойки:
2 10
2 9
1024
512
2 8
2 7
256
128
2 6
2 5
64
32
2 4
2 3
16
8
2 2
2 1
4
2
2 0
1
г) 84 10 = X 2
= 1100 001 2
а) 97 10 = X 2
= 1010100 2
д) 292 10 = X 2
= 101001000 2
= 100100100 2
б) 328 10 = X 2
в) 1090 10 = X 2
= 10001000010 2
е) 547 10 = X 2
= 1000100011 2
Комментарии
Количество и номера решаемых примеров на усмотрение учителя.
Задачи могут решаться самостоятельно или при фронтальной работе. Также можно организовать работу по вариантам.
Для удобства есть кнопка «Ответы», по которой выводятся ответы на все примеры сразу (без решения)
ОТВЕТ
Реши сам
Перевод десятичной дроби в систему счисления с основанием q
Для перевода конечной десятичной дроби в систему счисления с основанием q следует:
- последовательно умножать данное число и получаемые дробные части произведения на основание новой системы счисления до тех пор, пока дробная часть произведения не станет равна нулю или не будет достигнута требуемая точность представления числа;
- полученные целые части (цифры числа) привести в соответствие алфавиту новой системы счисления;
- составить дробную часть числа в новой системе счисления, начиная с целой части первого произведения.
= 0,011 2
№ 8. 0,375 10 = Х 2
Операция
0,375 · 2
Результат
0,75 · 2
0 ,750
0,5
1 ,500
1 ,000
0,375
0,5
0,75
х
х
х
2
2
2
?
1 ,0
1 ,50
0 ,750
Решите самостоятельно
№ 9. Переведите десятичные дроби в систему счисления с указанным основанием (с точностью до трех знаков после запятой):
= 0,110 2
= 0,100 8
= 0,5D7 16
а) 0,625 10 = X 2
= 0,101 2
г) 0,750 10 = X 2
б) 0,245 10 = X 8
= 0,175 8
д) 0,125 10 = X 8
= 0,75С 16
е) 0,365 10 = X 16
в) 0,460 10 = X 16
Комментарии
Количество и номера решаемых примеров на усмотрение учителя.
Задачи могут решаться самостоятельно или при фронтальной работе. Также можно организовать работу по вариантам.
Для удобства есть кнопка «Ответы», по которой выводятся ответы на все примеры сразу (без решения)
ОТВЕТ
Решите самостоятельно
№ 10. Переведите смешанные десятичные числа в систему счисления с указанным основанием (с точностью до трех знаков после запятой):
При переводе смешанных чисел из десятичной системы счисления в любую другую отдельно (по разным правилам) переводится целая и дробная части.
г) 43,125 10 = X 2
а) 98,75 10 = X 2
= 1100010,110 2
д) 16,78 10 = X 8
б) 100,375 10 = X 8
= 144,300 8
≈ 79,1EF 16
е) 750,750 10 = X 16
в) 121,121 10 = X 16
= 101011,001 2
≈ 20,617 8
= 2EE,C00 16
Комментарии
Количество и номера решаемых примеров на усмотрение учителя.
Задачи могут решаться самостоятельно или при фронтальной работе. Также можно организовать работу по вариантам.
Для удобства есть кнопка «Ответы», по которой выводятся ответы на все примеры сразу (без решения)
ОТВЕТ
Перевод чисел из системы счисления с основанием р в систему счисления
с основанием q
При необходимости перевод целого числа А из системы счисления с основанием p в систему счисления с основанием q можно свести к хорошо знакомым действиям с десятичной системе счисления: перевести исходное число в десятичную систему счисления, после чего полученное десятичное число представить в требуемой системе счисления.
Комментарии
Лупа – переход на скрытые слайды – второй способ перевода чисел (без участия 10-ной системы счисления). Данный способ может быть достаточно трудоемким, поэтому целесообразность его разбора учитель определяет сам
А 10
Развёрнутая запись (по степеням p )
Деление на q
А p
А q
q Все действия производятся в исходной системе счисления p. Делим число и полученные неполные частные на основание другой системы счисления до тех пор, пока неполное частное не станет равным нулю. Полученную в ходе деления последовательность остатков записываем в обратном порядке. = 22 3 Пример. 13 5 = Х 3 Все действия производим в 5-ной системе счисления. 3 13 Проверка: 13 5 = 1 · 5 + 3 = 8 10 22 3 = 2 · 3 + 2 = 8 10 3 11 2 0 0 2 2 " width="640"
Перевод целых чисел из системы счисления с основанием р в систему
счисления с основанием q
pq
- Все действия производятся в исходной системе счисления p.
- Делим число и полученные неполные частные на основание другой системы счисления до тех пор, пока неполное частное не станет равным нулю. Полученную в ходе деления последовательность остатков записываем в обратном порядке.
= 22 3
Пример. 13 5 = Х 3
Все действия производим в 5-ной системе счисления.
3
13
Проверка:
13 5 = 1 · 5 + 3 = 8 10
22 3 = 2 · 3 + 2 = 8 10
3
11
2
0
0
2
2
Перевод чисел из системы счисления с основанием р в систему
счисления с основанием q
p
1. Записать исходное число в развернутой форме:
a n · p n + a n-1 · p n-1 + ... + a 1 · p 1 + a 0 · p 0 , где p - старое основание.
2. Произвести вычисления в новой системе счисления q.
= 12 5
Пример. 21 3 = Х 5
Все действия производим в 5-ной системе счисления.
Проверка:
21 3 = 2 · 3 + 1 = 7 10
12 5 = 1 · 5 + 2 = 7 10
2 · 3 + 1 · 3 0
= 11 + 1 = 12 5
Быстрый перевод чисел в компьютерных системах счисления
Способ «быстрого» перевода основан на том, что каждой цифре числа в системе счисления, основание которой q кратно степени двойки, соответствует число, состоящее из n ( q=2 n ) цифр в двоичной системе счисления. Замена восьмеричных цифр двоичными тройками ( триадами ) и шестнадцатеричных цифр двоичными четвёрками ( тетра-дами ) позволяет осуществлять быстрый перевод. Для этого:
- данное двоичное число надо разбить справа налево на группы по n цифр в каждой;
- если в последней левой группе окажется меньше n разрядов, то её надо дополнить слева нулями до нужного числа разрядов;
- рассмотреть каждую группу как n-разрядное двоичное число и записать её соответствующей цифрой системы счисления с основанием q = 2 n .
Способ «быстрого» перевода основан на том, что каждой цифре числа в системе счисления, основание которой q кратно степени двойки, соответствует число, состоящее из n ( q=2 n ) цифр в двоичной системе счисления. Замена восьмеричных цифр двоичными тройками ( триадами ) и шестнадцатеричных цифр двоичными четвёрками ( тетра-дами ) позволяет осуществлять быстрый перевод.
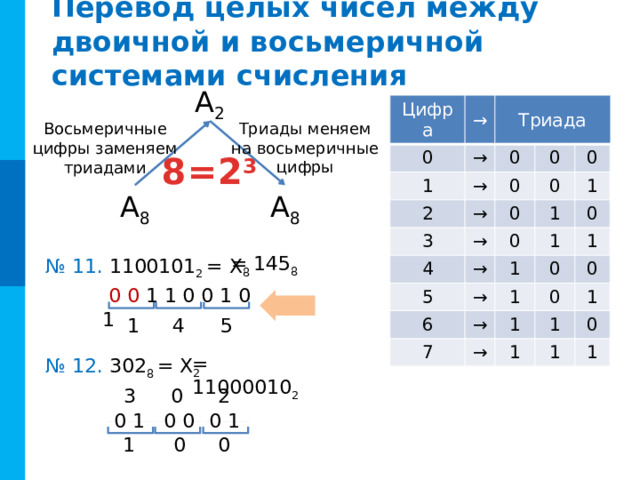
Перевод целых чисел между двоичной и восьмеричной системами счисления
А 2
Цифра
0
→
1
→
Триада
→
0
2
→
0
0
3
→
0
0
0
Цифра
4
0
1
0
1
→
→
5
Двоичный код
0
1
→
1
→
1
6
→
1
2
1
→
0
7
→
3
0
0
1
→
0
→
1
1
4
1
1
1
0
1
→
5
1
0
6
1
→
1
1
0
→
1
7
0
0
1
→
1
1
1
1
0
1
Триады меняем на восьмеричные цифры
Восьмеричные цифры заменяем триадами
8=2 3
А 8
А 8
= 145 8
№ 11. 1100101 2 = Х 8
0 0 1 1 0 0 1 0 1
1
4
5
= 11000010 2
№ 12. 302 8 = Х 2
3
0
2
0 1 1
0 0 0
0 1 0
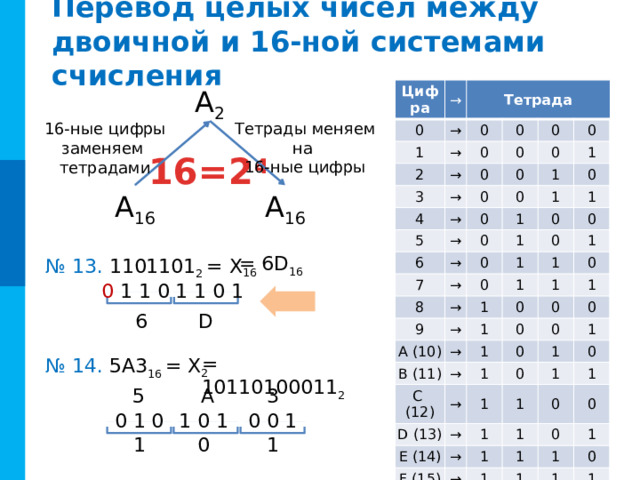
Перевод целых чисел между двоичной и 16-ной системами счисления
А 2
Цифра
Цифра
0
0
→
→
Двоичные коды
1
→
1
Тетрада
→
0
→
2
2
→
→
0
→
0
3
3
0
0
0
4
→
4
→
0
0
0
0
→
0
5
→
5
1
1
1
1
6
6
→
→
0
0
0
0
1
1
0
→
1
7
→
7
1
0
1
1
0
1
8
1
0
→
8
→
0
0
0
1
0
0
→
1
9
→
9
1
1
1
→
1
1
1
1
A (10)
→
A (10)
1
B (11)
1
0
0
1
→
1
0
B (11)
1
→
0
1
1
→
C (12)
0
0
1
0
0
C (12)
→
1
0
0
→
1
D (13)
0
0
1
0
D (13)
→
0
1
1
0
1
1
1
E (14)
E (14)
→
→
1
0
0
0
F (15)
1
1
1
1
1
→
1
→
F (15)
1
→
→
1
1
1
0
1
1
0
1
0
1
0
1
0
0
1
1
1
1
1
1
1
1
0
0
1
1
1
Тетрады меняем на 16-ные цифры
16-ные цифры заменяем тетрадами
16=2 4
А 16
А 16
= 6D 16
№ 13. 1101101 2 = Х 16
0 1 1 0 1 1 0 1
D
6
= 10110100011 2
№ 14. 5 A3 16 = Х 2
A
3
5
1 0 1 0
0 1 0 1
0 0 1 1
Реши сам
Перевод дробной части между двоичной и восьмеричной системами
Чтобы записать правильную двоичную дробь в системе счисления с основанием q = 2 n , достаточно:
1) двоичное число разбить слева направо на группы по n цифр в каждой; если в последней правой группе окажется меньше n разрядов, то её надо дополнить справа нулями до нужного числа разрядов;
2) рассмотреть каждую группу как n -разряд-ное двоичное число и записать её соответствующей цифрой.
Цифра
0
→
1
Триада
→
2
→
0
0
→
0
3
0
0
0
4
→
5
1
1
0
→
0
6
1
→
1
→
1
1
7
0
0
0
1
→
1
1
1
0
1
1
= 0,72 8
№ 15. 0, 11101 2 = Х 8
0, 1 1 1 0 1 0
2
7
0,
= 0,00101101 2
№ 16. 0,132 8 = Х 2
2
3
1
0,
?
0,
0 0 1
0 1 1
0 1 0
Решите самостоятельно
№ 17. Заполните таблицу: переве-дите число из одной системы счисления ( q ) в другую методом «быстрого» перевода:
Цифра
→
0
Двоичный код
→
1
2
0
→
→
0
0
3
0
0
0
4
→
0
0
0
→
0
5
1
1
0
→
0
6
0
7
→
0
1
1
1
0
0
→
1
8
0
0
1
→
0
9
А(10)
1
→
1
1
1
B(11)
0
0
1
1
→
1
1
→
0
0
C(12)
1
→
D(13)
0
0
0
0
→
1
1
E(14)
1
F(15)
→
0
1
1
1
1
→
1
1
0
1
0
0
1
1
1
1
1
0
1
q=2
q=16
q=8
705
111000101
1C5
111000110010
7062
E32
C0DE
1100000011011110
140336
11011,11
1B,С
33,6
2E,8
56,4
101110,1
470,1
100111000,001
138,2
ОТВЕТ
Самое главное
Для перевода целого десятичного числа в систему счисления с основанием q следует:
- последовательно выполнять деление данного числа и получаемых целых частных на основание новой системы счисления до тех пор, пока не получится частное, равное нулю;
- полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие алфавиту новой системы счисления;
- составить число в новой системе счисления, записывая его, начиная с последнего остатка.
Самое главное
В компьютерных науках широко используются двоичная, восьмеричная и шестнадцатеричная системы счисления, поэтому их называют «компьютерными». Между основания-ми этих систем существует очевидная связь: 16 = 2 4 , 8 = 2 3 .
Если основание системы счисления q кратно степени двойки ( q = 2 n ), то любое число в этой системе счисления можно «быстро» перевести в двоичную систему счисления, выписав последовательно двоичные коды каждой из цифр, образующих исходное число. Замена восьмеричных цифр двоичными тройками ( триадами ) и шестнадцатеричных цифр двоичными четвёрками ( тетрадами ) позволяет осуществлять быстрый перевод между этими системами счисления, не прибегая к арифметическим операциям.
5 . Следовательно, условию задачи удовлетворяют основания: 28 , 14 и 7 . Ответ: 28 , 14 и 7 . " width="640"
Вопросы и задания
Задание 1. Укажите через запятую в порядке убывания все основания систем счисления, в которых запись десятичного числа 33 оканчивается на 5 .
Решение:
Поскольку запись числа в системе счисления с основанием q заканчивается на 5 , то остаток от деления числа 33 на q равен пяти: 33 mod q = 5 .
Следовательно, ( 33-5) mod q = 0 , т.е. 28 mod q =0 .
Это верно для q ∈ { 28, 14, 7, 4, 2, 1 }.
Так как в новой системе счисления запись числа оканчивается на пять, то q 5 .
Следовательно, условию задачи удовлетворяют основания: 28 , 14 и 7 .
Ответ: 28 , 14 и 7 .
Вопросы и задания
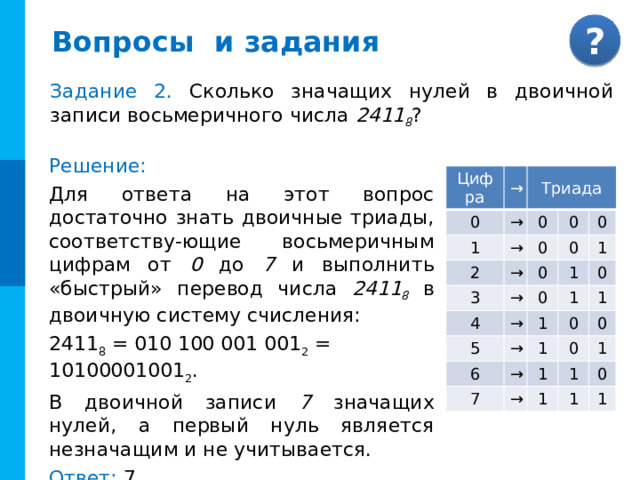
Задание 2. Сколько значащих нулей в двоичной записи восьмеричного числа 2411 8 ?
Решение:
Для ответа на этот вопрос достаточно знать двоичные триады, соответству-ющие восьмеричным цифрам от 0 до 7 и выполнить «быстрый» перевод числа 2411 8 в двоичную систему счисления:
2411 8 = 010 100 001 001 2 = 10100001001 2 .
В двоичной записи 7 значащих нулей, а первый нуль является незначащим и не учитывается.
Ответ: 7
Цифра
→
0
→
1
Триада
→
0
2
0
→
0
3
0
→
4
0
0
0
→
5
1
1
1
→
1
0
6
7
→
1
1
0
→
0
1
0
1
1
1
1
0
1
Вопросы и задания
Задание 3. Все 5-буквенные слова, составленные из букв А , Б и В , записаны в алфавитном порядке и пронумеро-ваны. Вот начало списка:
1. ААААА
2. ААААБ
3. ААААВ
4. АААБА
5. АААББ
…
Какие слова находятся в этом списке на 51-м и 200-м местах?
Решение:
Слово в трехбуквенном алфавите можно рассматривать, как запись слова в троичной системе в 5-разрядном представлении. Тогда А – 0, Б – 1, В – 2.
Вопросы и задания
Задание 3 (решение).
Аналогично надо перевести в троичную систему счисле-ния число 199.
А – 0, Б – 1, В – 2.
Чтобы понять, какое слово соответствует этому числу, надо перевести его в троич-ную систему счисления и при необходимости дополнить слева «0» до пяти разрядов.
При такой записи незнача-щие нули в начале (слева) тоже записываются:
1. ААААА
2. ААААБ
3. ААААВ
4. АААБА …
51. ?
200. ?
3
199
= 00000 3 = 0 10
= 00001 3 = 1 10
= 00002 3 = 2 10
= 00010 3 = 3 10 …
3
198
66
3
22
66
1
3
21
7
0
3
50
3
2
6
1
3
48
16
0
0
1
= ***** 3 = 50 10
= ***** 3 = 199 10
3
5
15
2
2
3
3
1
1
0
0
2
→ ВББАБ
199 10 = 21101 3
На 51-м месте в списке стоит число 51-1 = 50, а на 200-м – число 200-1=199.
1
Ответ: АБВБВ и ВББАБ
50 10 = 01212 3
→ АБВБВ
Вопросы и задания
Задание 4. Все 5-буквенные слова, составленные из букв А , Б и В , записаны в алфавитном порядке и пронумеро-ваны. Вот начало списка:
1. ААААА
2. ААААБ
3. ААААВ
4. АААБА
5. АААББ
…
На каких местах будут стоять слова АБВБА и ВВВВВ?
Ответ: 49 и 243
ОТВЕТ
© 2025, Донченко Виктория Геннадиевна 100 0
Рекомендуем курсы ПК и ППК для учителей
Похожие файлы
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
Полезное для учителя
Реализация образовательных программ осуществляется с применением исключительно электронного обучения и ДОТ
Закрыть через 5 секунд
