Муниципальное бюджетное общеобразовательное учреждение
г. Керчи Республики Крым
«Школа №4 имени А.С. Пушкина»
Теорема Пифагора
Автор:
Свистельников И.В.,
обучающийся 8 класса
МБОУ г. Керчи РК
«Школа №4 им. А.С. Пушкина»
Руководитель:
Мирошниченко Т.А.,
учитель математики
высшей квалификационной
категории
Керчь, 2018
Содержание
Тезисы.....................................................................................................3
Введение…………………………………………………………….….4
Глава 1. Пифагор ...................................................................................5
Исторические сведения………………………………….....…...5
Школа Пифагора и пифагорейцы………………………….…...6
Глава 2. Характеристика теоремы…………………….………….…...7
2.1. Предыстория теоремы……………………………………….........7
2.2. Идеи о доказательстве теоремы……………………………….…..8
Глав 3. Некоторые способы доказательства………………….………10
3.1. Геометрическое доказательство (метод Гофмана) .....................10
3.2. Доказательство по площади............................................................11
Глава 4. Применение теоремы Пифагора…………………………….12
4.1. Мобильная связь..............................................................................12
4.2. Молниеотвод....................................................................................12
4.3. Окна...................................................................................................13
4.4. Астрономия.......................................................................................13
4.5. Строительство крыш .......................................................................14
Заключение ..............................................................................................15
Тезисы
Цель работы
Доказать значение теоремы Пифагора в развитие науки и техники многих стран и народов мира, а также показать интересные формы доказательства теоремы.
Задачи
Изучить необходимую литературу о значении и роли теоремы Пифагора.
Познакомиться с историей возникновения теоремы.
Познакомиться с некоторыми способами доказательства теоремы.
Провести работу по исследованию применения теоремы.
Вывод нашего исследования
Теорема Пифагора- одна из самых важных теорем геометрии. Из нее или с ее помощью можно вывести большинство теорем геометрии.
Теорема Пифагора была первым утверждением, связавшим длины сторон треугольников. Потом узнали, как находить длины сторон и углы остроугольных и тупоугольных треугольников. Возникла целая наука тригонометрия (“тригон” – по-гречески означает “треугольник”).
Таким образом, в результате проведенного исследования установлено
Что теорема Пифагора позволяет найти длину отрезка(гипотенузы), не измеряя его непосредственно, она как бы открывает путь с прямой на плоскость, с плоскости в трёхмерное пространство и дальше – в многомерные пространства. Этим определяется ее исключительная важность для геометрии и математики в целом.
Название работы Теорема Пифагора
Автор Обучающийся 8-В класса МБОУ г. Керчи РК «Школа №4 им. А.С. Пушкина» Свистельников И.В.
Руководитель Учитель математики высшей квалификационной категории Мирошниченко Т.А.
Муниципальное бюджетное общеобразовательное учреждение г. Керчи Республики Крым «Школа №4 имени А.С. Пушкина»
3
Введение
Трудно найти человека, у которого имя Пифагор не ассоциировалось бы с его теоремой. Пожалуй, даже те, кто в своей жизни навсегда распрощался с математикой, сохраняют воспоминание о “пифагоровых штанах” - квадрате на гипотенузе, равновеликом двум квадратам на катетах.
Причина такой популярности теоремы Пифагора триедина: это простота-красота-значимость. В самом деле, теорема Пифагора проста, но не очевидна. Это сочетание двух противоречивых начал придает ей особую притягательную силу, делает ее красивой.
Кроме того, теорема Пифагора имеет огромное значение: она применяется в геометрии буквально на каждом шагу, и тот факт, что существует около 500 различных доказательств этой теоремы (геометрических, алгебраических, механических и т. д.), свидетельствует о гигантском числе ее конкретных реализаций.
В современных учебниках теорема сформулирована так: “В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов”.
Во времена Пифагора она звучала так: “Доказать, что квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на катетах” или “Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах”.
Область исследования – геометрия.
Объект исследования Теорема Пифагора
Предмет исследования Применение теоремы Пифагора
Цель работы Доказать значение теоремы Пифагора в развитие науки и техники многих стран и народов мира, а также показать интересные формы доказательства теоремы.
Задачи
Изучить необходимую литературу о значении и роли теоремы Пифагора.
Познакомиться с историей возникновения теоремы.
Познакомиться с некоторыми способами доказательства теоремы.
Провести работу по исследованию применения теоремы.
4
Методы
При выполнении данной работы использовались теоретические и практические методы: анализ научной литературы по вопросу; систематизация и обработка данных.
Этапы
1)Теоретический - изучение и анализ литературы.
2)Практический – показать значение теоремы Пифагора в развитии науки и техники многих стран и народов мира.
Основная часть
Глава 1
Пифагор
Древнегреческий философ и математик, прославившийся своим учением о космической гармонии и переселении душ. Предание приписывает Пифагору доказательство теоремы, носящей его имя. Многое в учении Платона восходит к Пифагору и его последователям.
Пифагору также приписывается высказывание: “Все есть число”. К числам (а он имел ввиду лишь натуральные числа) он хотел свести весь мир, и математику в частности. С именем Пифагора связывают учения об арифметических, геометрических и гармонических пропорциях.
1.1.Исторические сведения
Древнегреческий философ, родился в 570 г. до н.э. на острове Самос. Много путешествовал по востоку, именно там он познакомился с восточной математике.
Известно что Пифагор покинул свой родной остров и в 40 лет, в знак протеста против тирании правителя появился в греческом городе Кротоне на юге Италии. Пифагор и его последователи- пифагорейцы- образовали тайный союз, игравший немалую роль в жизни греческих колоний в Италии.
Пифагорейцы узнавали друг друга по звёздчатому пятиугольнику – пентаграмме. Но Пифагору пришлось удалиться в Метапонт, где он и умер.
Пифагор-это не имя, а прозвище, данное ему за то, что он высказывал истину, так же постоянно, как дельфийский оракул.
“Пифагор”- значит “Убеждающий речью”
5 .

Пифагор – это не только великий философ,
но и великий математик своего времени.
И, конечно же, одна из самых главных заслуг Пифагора – это доказательство теоремы,
которая носит его имя.
1.2.Школа Пифагора и пифагорейцы
Труды, обычно приписываемые Пифагору, относятся не только к легендарному Пифагору, но вообще к трудам его школы, которая существовала в период с 585 до 400 гг. до н.э
Эта школа заложила основу греческой арифметики, которая ограничивалась изучением целых чисел. Их арифметика геометрична, она разбивает числа в зависимости от формы соответствующих им фигур из точек на треугольные, квадратные, пятиугольные и т.д. Пифагорейцы верили, что в числовых закономерностях спрятана тайна мира. Мир чисел жил для пифагорейца особой жизнью, числа имели свой особый жизненный смысл. Числа, равные сумме делителей, воспринимались как совершенные (6 ,28, 496, 8128).
Попасть в школу было не просто.
Претендент должен был выдержать ряд испытаний, одним из таких испытаний являлся обет пятилетнего молчания, и все это время принятые в школу могли слушать голос учителя лишь из-за занавеса, а увидеть могли только тогда, когда их "души будут очищены музыкой и тайной гармонией чисел".
Другим законом организации было хранение тайны, несоблюдение которой строго каралось – вплоть до смерти. После того как школу Пифагора перестала существовать, его ученики поступили в другие школы тех времён (например в школу Евклида ).
6
Глава 2. Характеристика теоремы
Теорема Пифагора имеет огромное значение: она применяется в геометрии буквально на каждом шагу, и тот факт, что существует около 500 различных доказательств этой теоремы (геометрических, алгебраических, механических и т. д.), свидетельствует о гигантском числе ее конкретных реализаций.
2.1.Предыстория теоремы
Открытие теоремы Пифагора окружено ореолом красивых легенд. Прокл, комментируя последнее предложение 1-ой книги “Начал” Евклида, пишет: “Если послушать тех, кто любит повторять древние легенды, то придется сказать, что это теорема восходит к Пифагору; рассказывают, что он в честь этого принес в жертву быка”. Легенда эта прочно срослась с теоремой Пифагора и через 2000 лет продолжала вызывать горячие отклики.
Теорема
Теорема Пифагора— одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника. Традиционно, авторство теоремы приписывают греческому философу и математику Пифагору, хотя сохранились убедительные свидетельства того, что теорема была известна задолго до него.
Древний Китай
Исторический обзор начнем с древнего Китая. Здесь особое внимание привлекает математическая книга Чу-пей. В этом сочинении так говорится о пифагоровом треугольнике со сторонами 3, 4 и 5:
"Если прямой угол разложить на составные части, то линия, соединяющая концы его сторон, будет 5, когда основание есть 3, а высота 4".
В этой же книге предложен рисунок, который совпадает с одним из чертежей индусской геометрии Басхары.
Древний Египет
Кантор (крупнейший немецкий историк математики) считает, что равенство 3² + 4² = 5²
7
было известно уже египтянам еще около 2300 г. до н. э., во времена царя Аменемхета I (согласно папирусу 6619 Берлинского музея).
По мнению Кантора гарпедонапты, или "натягиватели веревок", строили прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5.
Очень легко можно воспроизвести их способ построения. Возьмем веревку длиною в 12 м. и привяжем к ней по цветной полоске на расстоянии 3 м. от одного конца и 4 метра от другого.
Прямой угол окажется заключенным между сторонами длиной в 3 и 4 метра. Гарпедонаптам можно было бы возразить, что их способ построения становиться излишним, если воспользоваться, например, деревянным угольником, применяемым всеми плотниками. И действительно, известны египетские рисунки, на которых встречается такой инструмент, например рисунки, изображающие столярную мастерскую.
Вавилон
Несколько больше известно о теореме Пифагора у вавилонян. В одном тексте, относимом к 2000 г. до н. э., приводится приближенное вычисление гипотенузы прямоугольного треугольника. Отсюда можно сделать вывод, что в Двуречье умели производить вычисления с прямоугольными треугольниками, по крайней мере в некоторых случаях.
Основываясь, с одной стороны, на сегодняшнем уровне знаний о египетской и вавилонской математике, а с другой- на критическом изучении греческих источников, Ван-дер-Варден (голландский математик) сделал следующий вывод:
"Заслугой первых греческих математиков, таких как Фалес, Пифагор и пифагорейцы, является не открытие математики, но ее систематизация и обоснование. В их руках вычислительные рецепты, основанные на смутных представлениях, превратились в точную науку."
Геометрия у индусов, как и у египтян и вавилонян, была тесно связана с культом. Весьма вероятно, что теорема о квадрате гипотенузы была известна в Индии уже около 18 века до н. э.
2.2. Идея о доказательстве теоремы
Открытие и понимание теоремы протекало в несколько этапов:
8
Алгебраическое наблюдение существования Пифагоровых троек (прямоугольных треугольников с целочисленными сторонами), то есть численная проверка того, что квадрат длины гипотенузы оказывается равным сумме квадратов длин катетов.
Б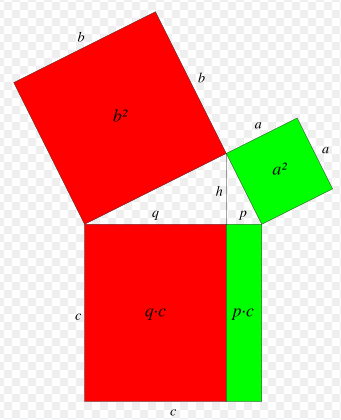 олее глубокое понимание теоремы, связанное с понятием площади и основанные на этом доказательства, например доказательства путём перестановки.
олее глубокое понимание теоремы, связанное с понятием площади и основанные на этом доказательства, например доказательства путём перестановки.
Доказательства, основанные на евклидовой геометрии, в частности, доказательство методом подобия треугольников, а также доказательство Евклида
В то же время, такие известные авторы как Плутарх и Цицерон приписывают авторство теоремы именно Пифагору, в соответствии с этими источниками можно сделать вывод о том, что авторство Пифагора было широко известно и не подвергалось сомнению.
Согласно комментариям Прокла к трудам Евклида: Пифагор, чьи годы жизни обычно даются в рамках 569 и 475 годы до нашей эры, использовал алгебраические методы для конструкции пифагоровых троек. Комментарии Прокла датируются 410 и 485 годами до нашей эры соответственно.
В школе Пифагора были подробно изучены так называемые Пифагоровы тройки натуральных чисел. Это числа, для которых справедливо равенство
a2+b2=c2 ( a,b,c - натуральные числа)
Таковы, например, числа 3, 4, 5. Все тройки взаимно простых пифагоровых чисел можно получить по формулам:
a=2n+1 b=2n(n+1) c=2n(1 +n)+1,
где n- натуральное числа
В те времена считали, что стороны каждого прямоугольного треугольника можно выразить пифагоровыми числами. Однако уже пифагорейцами было доказано, что это не так. Действительно, при a=b=1 гипотенузу нельзя выразить ни целым, ни дробным числом. Этот факт послужил толчком к открытию иррациональных чисел, являющихся основой современной математики. Можно предположить, что это и послужило толчком к выводу доказательства той самой теоремы, которой было присвоено имя Пифагора.
9
Сегодня известно около 500 различных доказательств теоремы Пифагора геометрических, алгебраических, механических и прочих.
Глава 3. Некоторые способы доказательства
3.1.Геометрическое доказательство (метод Гофмана)

Построим треугольник ABC с прямым углом С.
Построим BF=CB, BF^CB
лро
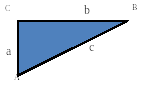

Построим BE=AB, BE^AB
Построим AD=AC, AD^AC
Точки F, C, D принадлежат одной прямой.
Как мы видим, четырёхугольники ADFB и ACBE равновелики, т.к. треугольники ABF=ЕCB. Треугольники ADF и ACE равновелики.
Отнимем от обоих равновеликих четырёхугольников общий для них треугольник ABC, получим:
1/2а2+1/2b 2=1/2с2
Соответственно:
а2+ b2 =с2
Теорема доказана!!!
10
 3.2.Доказательство по площади
3.2.Доказательство по площади
Опустим высоту на
гипотенузу C .Площадь

треугольника-S , b c
разбивается на 2 S1
Ему подобных с площадями S2
S1 и S2.
a
Площади треугольников относятся как
Квадраты их гипотенуз.

НО
 S1:S2:S=a2:b2:c2
S1:S2:S=a2:b2:c2
S1+S2=S ,то есть a2+b2=c2
Теорема доказана!!!
11
Глава 4. Применение теоремы Пифагора
4.1.Мобильная связь
К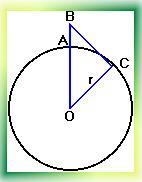 акую наибольшую высоту должна иметь антенна мобильного оператора, чтобы передачу можно было принимать в радиусе R=200 км? (радиус Земли равен 6380 км.)
акую наибольшую высоту должна иметь антенна мобильного оператора, чтобы передачу можно было принимать в радиусе R=200 км? (радиус Земли равен 6380 км.)
Решение:
Пусть AB=x, BC=R=200 км, OC=r=6380 км.
OB=OA+AB
OB= r + x.
Используя теорему Пифагора, получим 23 км.
Ответ: 23 км.
4.2.Молниеотвод
И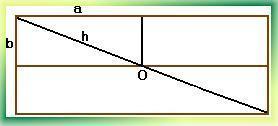 звестно, что молниеотвод защищает от молнии все предметы, расстояние которых от его основания не превышает его удвоенной высоты. Необходимо определить оптимальное положение молниеотвода на двускатной крыше, обеспечивающее наименьшую его доступную высоту.
звестно, что молниеотвод защищает от молнии все предметы, расстояние которых от его основания не превышает его удвоенной высоты. Необходимо определить оптимальное положение молниеотвода на двускатной крыше, обеспечивающее наименьшую его доступную высоту.
Решение:
По теореме Пифагора h2≥a2+b2, значит h≥(a2+b2) .
12
4.3.Окна
В романской архитектуре часто встречается мотив, представленный на рисунке. Если b по-прежнему обозначает ширину окна, то радиусы полуокружностей будут равны R = b/2 и r = b/4. Радиус p внутренней окружности можно вычислить из прямоугольного треугольника, изображенного на рис. пунктиром. Гипотенуза этого треугольника, проходящая через точку касания окружностей, равна b/4+p, один катет равен b/4, а другой b/2-p. По теореме Пифагора имеем:
(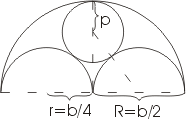 b/4+p)2=( b/4)2+( b/4-p)2
b/4+p)2=( b/4)2+( b/4-p)2
или
b/16+ bp/2+p=b/16+b/4-bp+p,
откуда
bp/2=b/4-bp.
Разделив на b и приводя подобные члены, получим:
(3/2)p=b/4, p=b/6.

4.4.Астрономия
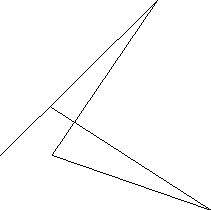
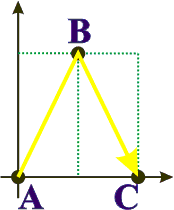
На этом рисунке показаны точки A и B
и путь светового луча от A к B и обратно.
Путь луча показан изогнутой стрелкой
для наглядности, на самом деле,
световой луч - прямой.
Какой путь проходит луч? Поскольку
свет идет туда и обратно одинаковый
путь, спросим сразу: чему равно расстояние между точками?
На этом рисунке показан путь светового луча только с другой точки зрения, например из космического корабля.Предположим, что корабль движется влево. Тогда две точки, между которыми движется
13
 световой луч, станут двигаться вправо с той
световой луч, станут двигаться вправо с той
же скоростью. Причем, в то время, пока луч пробегает
свой путь, исходная точка A смещается и луч
возвращается уже в новую точку C.
В конце девятнадцатого века высказывались разнообразные предположения о существовании обитателей Марса подобных человеку. В шутку, хотя и не совсем безосновательно, было решено передать обитателям Марса сигнал в виде теоремы Пифагора. Неизвестно, как это сделать; но для всех очевидно, что математический факт, выражаемый теоремой Пифагора имеет место всюду и поэтому похожие на нас обитатели другого мира должны понять такой сигнал.
4.5.Строительство крыш
При строительстве домов и коттеджей часто встает вопрос о длине стропил для крыши, если уже изготовлены балки. Например: в доме задумано построить двускатную крышу (форма в сечении). Какой длины должны быть стропила, если изготовлены балки АС=8 м., и AB=BF.
Решение:
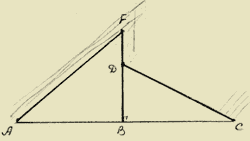 Треугольник ADC - равнобедренный AB=BC=4 м., BF=4 м. Если предположить, что FD=1,5 м., тогда
Треугольник ADC - равнобедренный AB=BC=4 м., BF=4 м. Если предположить, что FD=1,5 м., тогда
А) Из треугольника DBC: DB=2,5 м.,
Б) Из треугольника ABF:

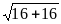
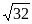
14
Заключение
Теорема Пифагора лежит в основе большинства геометрических вычислений. Еще в Древнем Вавилоне с ее помощью вычисляли длину высоты равнобедренного треугольника по длинам основания и боковой стороны, стрелку сегмента - по диаметру окружности и длине хорды, устанавливали соотношения между элементами некоторых правильных многоугольников. Теорема и уравнение Пифагора на протяжении тысячелетий привлекают внимание математиков, являясь источником плодотворных идей и открытий. В повседневной жизни нам часто приходится решать задачи на теорему Пифагора: в строительстве и машиностроении при проектировании любых строительных объектов.
15








 олее глубокое понимание теоремы, связанное с понятием площади и основанные на этом доказательства, например доказательства путём перестановки.
олее глубокое понимание теоремы, связанное с понятием площади и основанные на этом доказательства, например доказательства путём перестановки. 


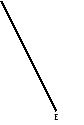

 3.2.Доказательство по площади
3.2.Доказательство по площади

 S1:S2:S=a2:b2:c2
S1:S2:S=a2:b2:c2  акую наибольшую высоту должна иметь антенна мобильного оператора, чтобы передачу можно было принимать в радиусе R=200 км? (радиус Земли равен 6380 км.)
акую наибольшую высоту должна иметь антенна мобильного оператора, чтобы передачу можно было принимать в радиусе R=200 км? (радиус Земли равен 6380 км.) звестно, что молниеотвод защищает от молнии все предметы, расстояние которых от его основания не превышает его удвоенной высоты. Необходимо определить оптимальное положение молниеотвода на двускатной крыше, обеспечивающее наименьшую его доступную высоту.
звестно, что молниеотвод защищает от молнии все предметы, расстояние которых от его основания не превышает его удвоенной высоты. Необходимо определить оптимальное положение молниеотвода на двускатной крыше, обеспечивающее наименьшую его доступную высоту. 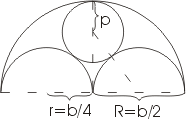 b/4+p)2=( b/4)2+( b/4-p)2
b/4+p)2=( b/4)2+( b/4-p)2 
 световой луч, станут двигаться вправо с той
световой луч, станут двигаться вправо с той Треугольник ADC - равнобедренный AB=BC=4 м., BF=4 м. Если предположить, что FD=1,5 м., тогда
Треугольник ADC - равнобедренный AB=BC=4 м., BF=4 м. Если предположить, что FD=1,5 м., тогда