План-конспект урока алгебры в 11 классе по теме "Решение систем уравнений" (профильный уровень)

Урок – практикум по теме

«Решение систем уравнений»

Урок алгебры в 11 «Д» классе

Провела учитель

математики

Чистова М.А.

МБОУ «Лицей «МОК №2»

г. Воронеж

Цели урока:

1. развитие системы знаний о методах решения систем уравнений высокого уровня сложности (уровень С5);

2. повторить алгоритм разложения многочлена на множители с помощью следствия теоремы Безу, деление многочлена на многочлен с помощью схемы Горнера, применение производной при решении целых уравнений, графический метод решения уравнений;

3. формирование ответственности при выполнении индивидуальных заданий, стимулирование поисковой деятельности, повышение культуры математического языка.

1. Организационный момент.

На боковой доске записано условие задачи ЕГЭ-2007:

С5. Доказать, что система уравнений

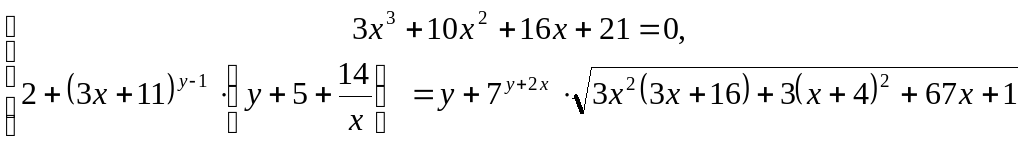
не имеет решений.

Сегодня на уроке мы рассмотрим решение данной задачи. На данный момент у каждого из вас эта система вызывает только отрицательные эмоции: пугает сложная структура второго уравнения, не понятно, с чего начать решение. Но я абсолютно уверена, что к концу урока у каждого из вас появится уверенность в том, что возможно справится с подобной задачей самостоятельно.

Решение всех задач уровня С5 требует значительных временных затрат.

Поэтому для того, чтобы ускорить процесс решения задачи и, самое главное, чтобы вы увидели четкий план ее решения, к этому уроку были даны индивидуальные задания:

1. Найти ОДЗ выражения .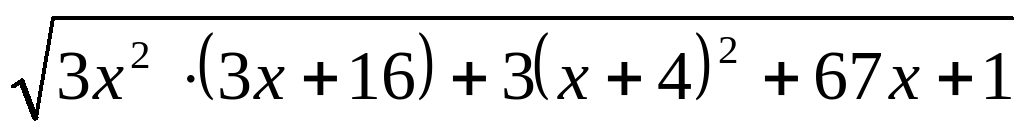

1. Сколько корней имеет уравнение ?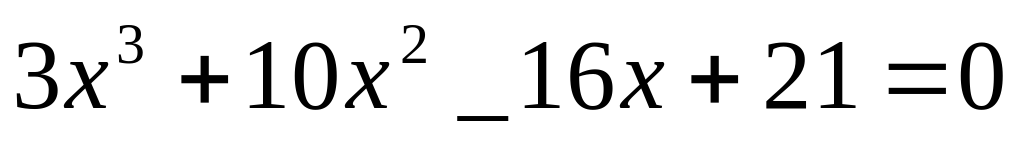

1. Решить уравнение .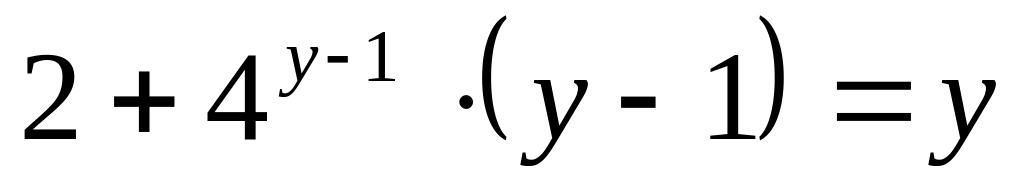

2.Решение.

1. Найдем ОДЗ данной системы.

1-ый ученик:

Преобразуем подкоренное выражение к виду 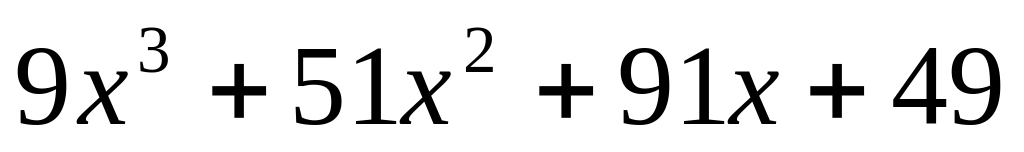и разложим его на множители, используя следствия из теоремы Безу:

X=-1 корень многочлена, значит, он делится на 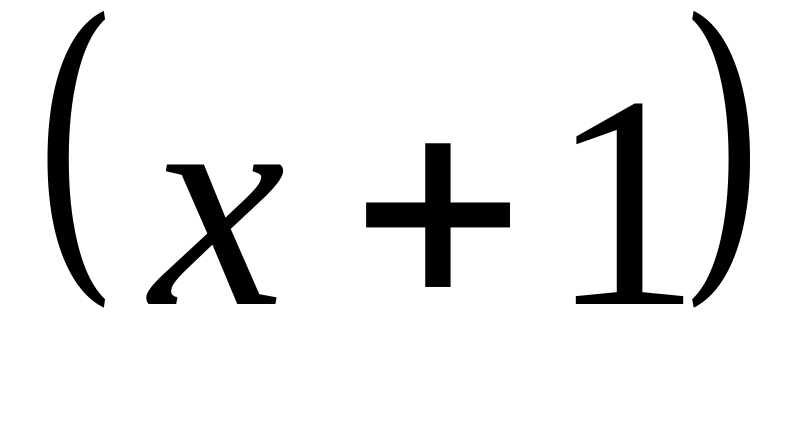. Воспользуемся схемой Горнера: 9 51 91 49

-1 9 42 49 0.

.

Таким образом, ОДЗ исходной системы: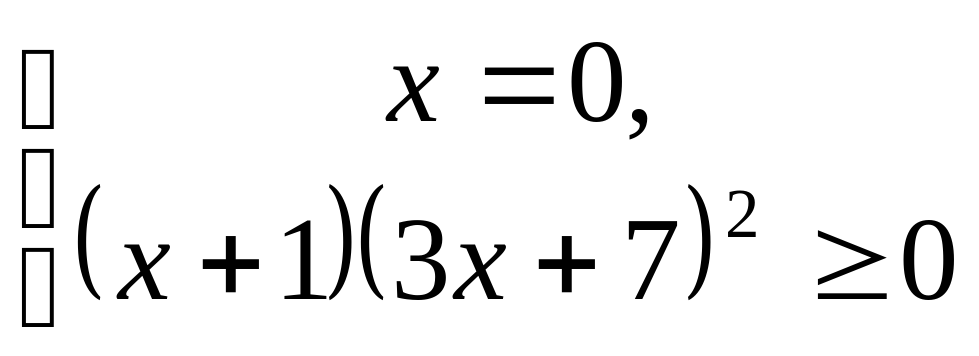

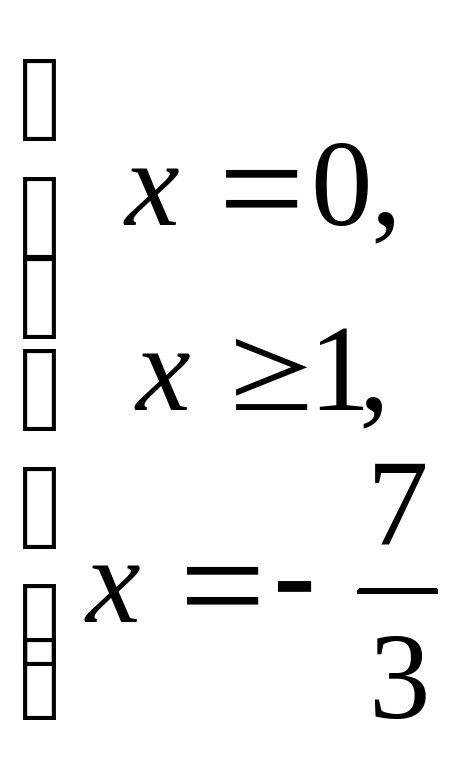
2) Попытаемся решить первое уравнение системы.

2-ой ученик: (предварительно рассказывает о своих попытках определить количество корней уравнения другими способами, которые не увенчались успехом).

Рассмотрим функцию ;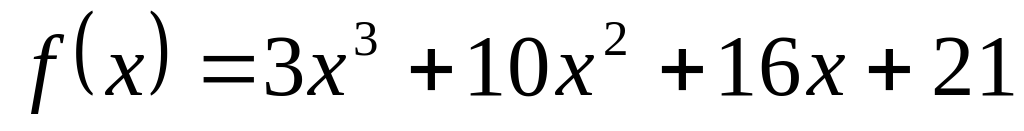

;

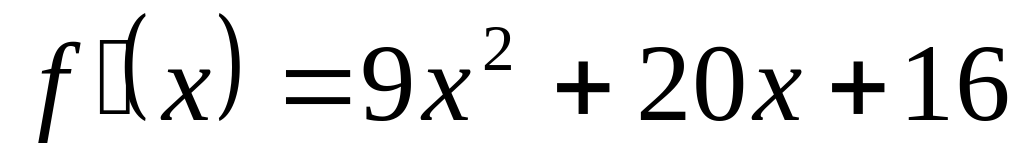Д 0, следовательно, 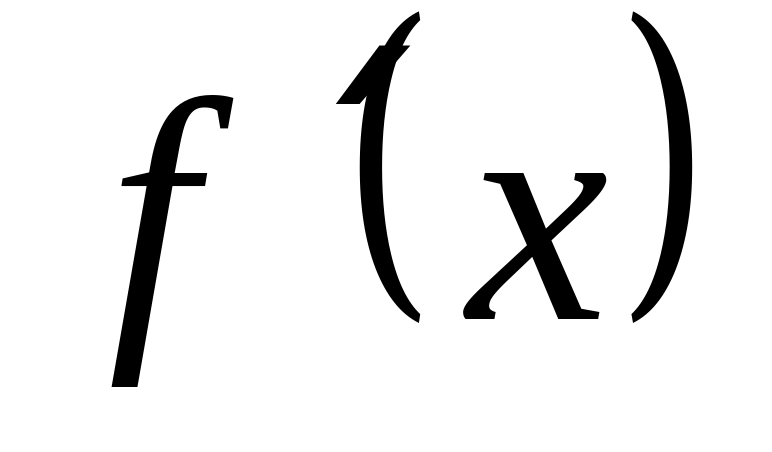принимает только положительные значения, значит, 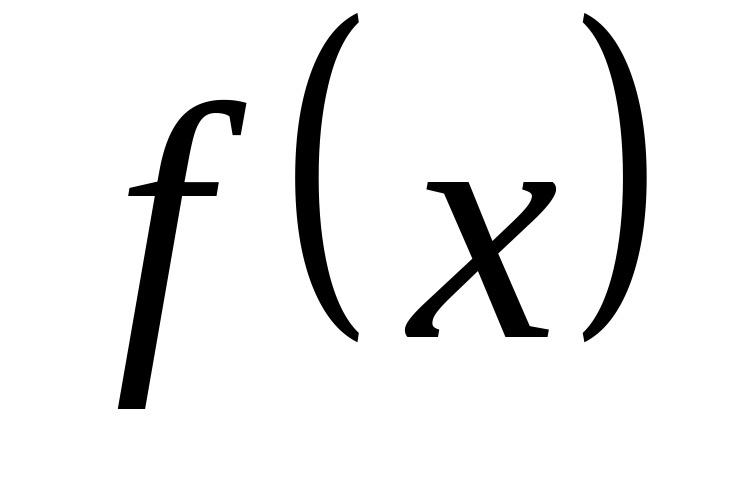возрастает на всей области определения и уравнение 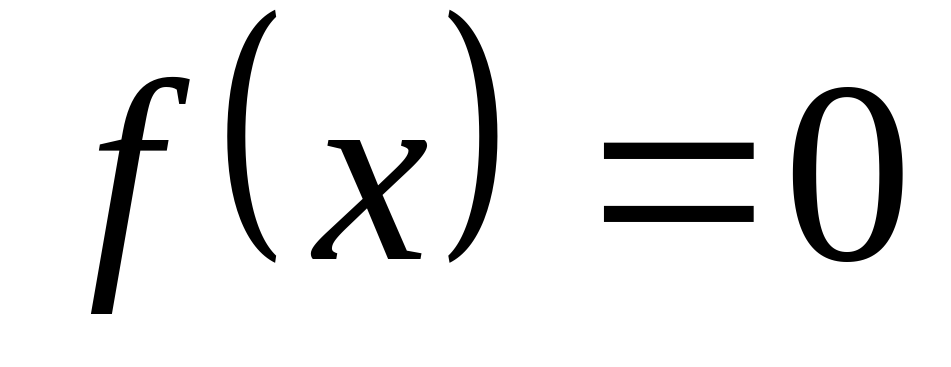имеет не более одного корня.

3)Искомый корень должен принадлежать ОДЗ системы.

х = 1 не является корнем (уже проверяли), проверим х = .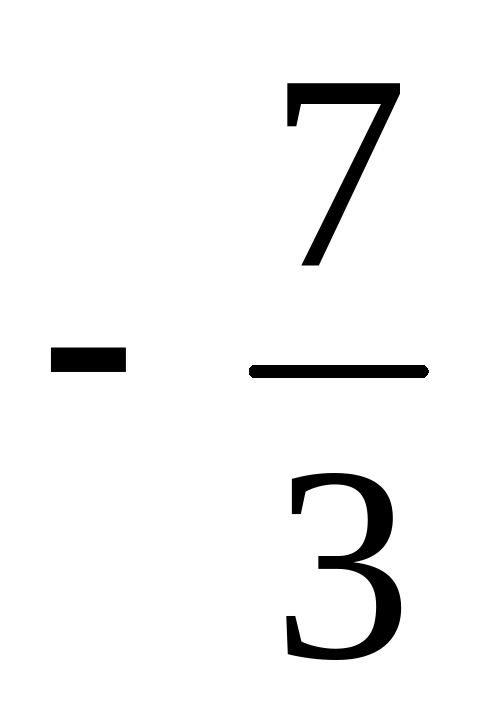

Проверка показывает, что данное число является корнем.

Итак, 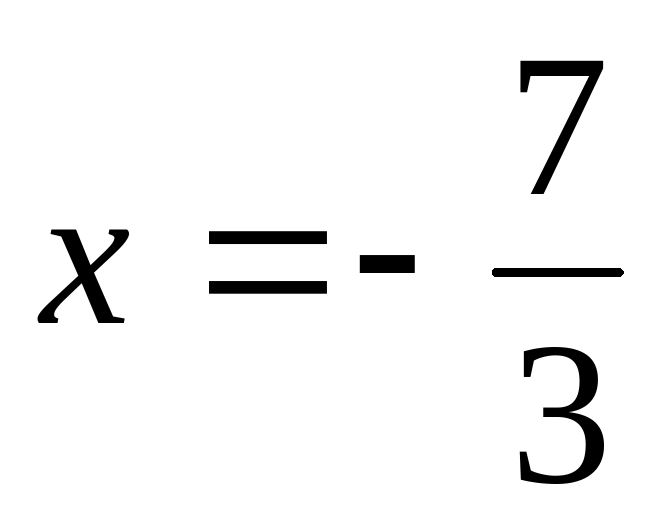корень первого уравнения системы и 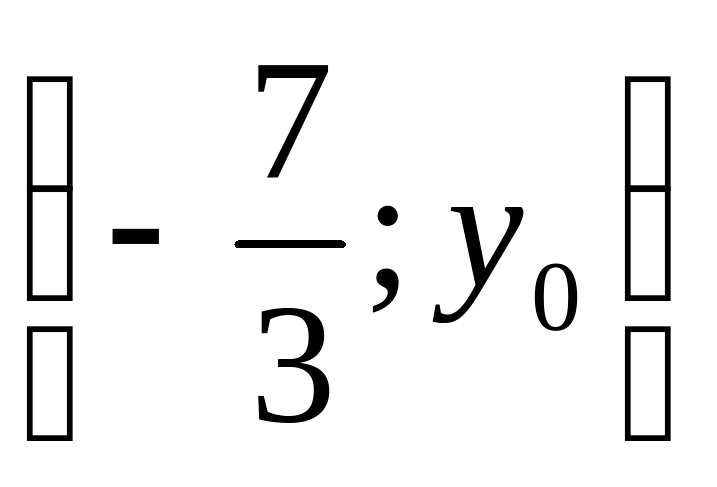- решение системы.

4)Подставим найденное значение x во второе уравнение системы и получим следующее:

.

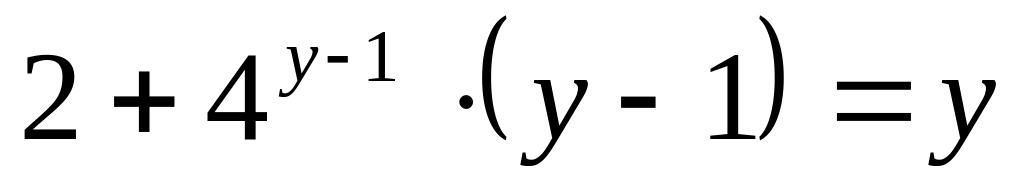3-ий ученик:

Так как у = 1 не является корнем уравнения, разделим обе его части на ,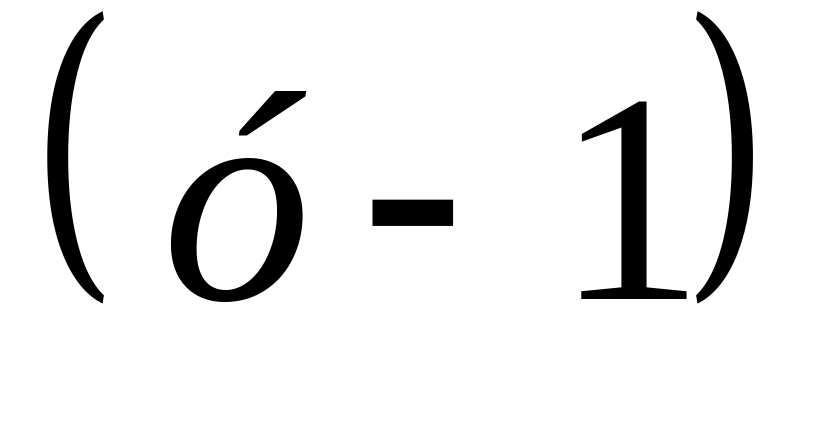

получим: 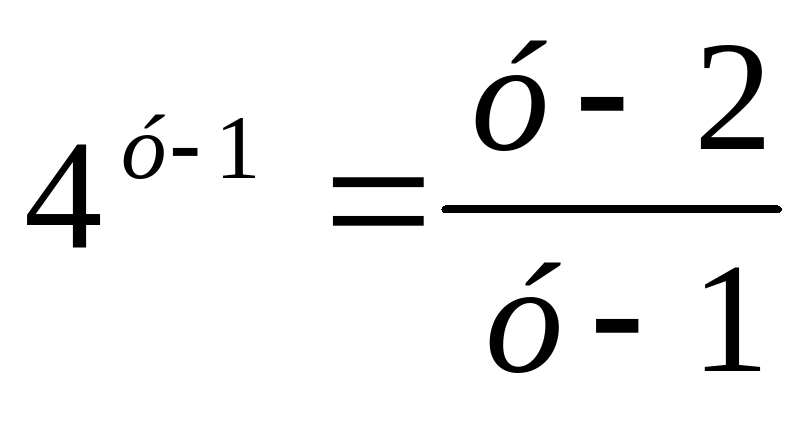или .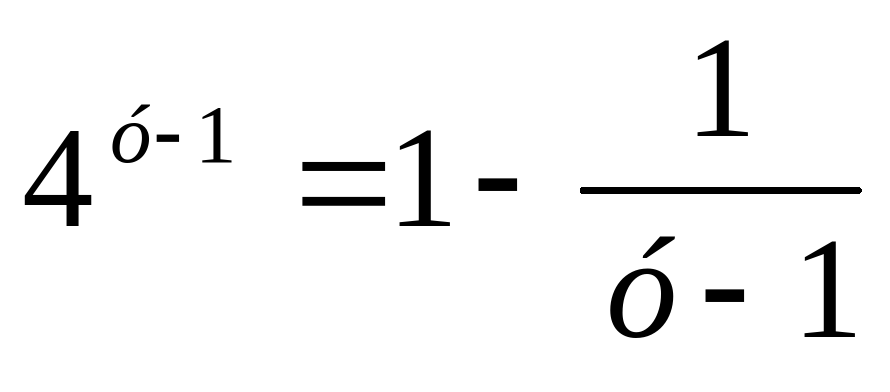

Решим это уравнение графически.

Гипербола и экспонента не пересекаются, следовательно, данное уравнение не имеет корней.

Таким образом, 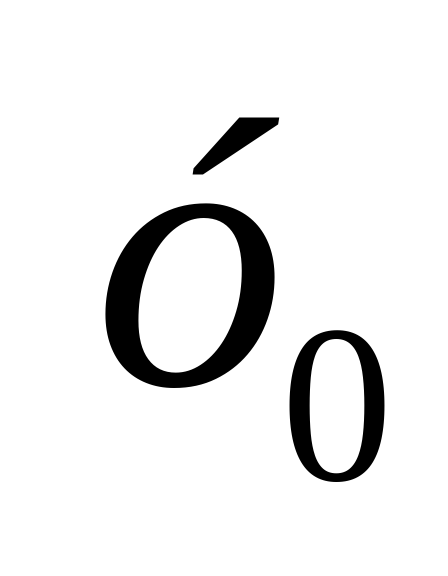не существует и система решений не имеет. Задача решена.

3. Подведение итогов, рефлексия.

Сформулировать поэтапный ход решения задачи (в виде плана).

Что повторили в ходе решения задачи?

Какой этап решения показался наиболее сложным?

Появилась ли уверенность?

Какие выводы можно сделать относительно задач уровня С, предлагаемых

на ЕГЭ?

В качестве домашнего задания предлагается аналогичная задача.