Тема: Площадь криволинейной трапеции (2ч)
Цель занятия:
ввести понятие криволинейной трапеции,
сформулировать теорему о нахождении площади криволинейной трапеции,
познакомить с понятием интеграла.
формировать умения делать выводы.
формировать интерес к изучению математики.
развивать творческую активность студентов.
Ход занятия
Криволинейной трапецией называется фигура, ограниченная графиком неотрицательной и непрерывной на отрезке [a;b] функции f, осью Ox и прямыми x = a и x = b.
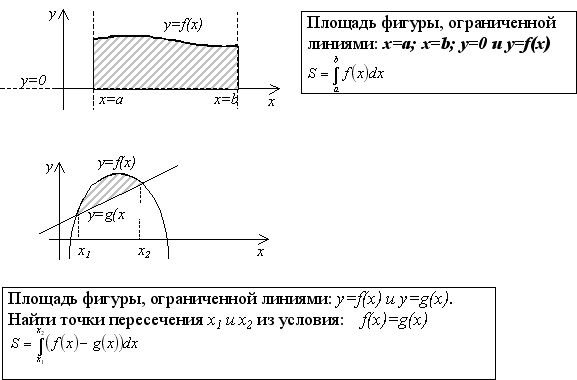
Выполнение упражнений
Итоги занятия
Домашнее задание
По учебнику «Алгебра и начала анализа» 10-11клас. А.Н. Колмогоров стр. 179-183
Тема: Интеграл. Формула Ньютона-Лейбница (4ч)
Цель занятия:
Ознакомить с понятием интеграла и формулой Ньютона-Лейбница;
Закрепить понятие интеграла и знание формулы Ньютона-Лейбница;
Научить применять формулу и понятие интеграла для решения примеров;
Научить вычислять определенный интеграл;
Формировать умение и навык нахождения интеграла функции;
Ход занятия
Пусть функция y = f(x) непрерывна на отрезке [a; b] и F(x) - одна из первообразных функции на этом отрезке, тогда справедлива формула Ньютона-Лейбница: 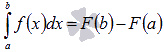 .
.
Формулу Ньютона-Лейбница называют основной формулой интегрального исчисления.
Для доказательства формулы Ньютона-Лейбница нам потребуется понятие интеграла с переменным верхним пределом.
Если функция y = f(x) непрерывна на отрезке [a; b], то для аргумента 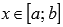 интеграл вида
интеграл вида 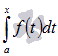 является функцией верхнего предела. Обозначим эту функцию
является функцией верхнего предела. Обозначим эту функцию 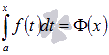 , причем эта функция непрерывная и справедливо равенство
, причем эта функция непрерывная и справедливо равенство 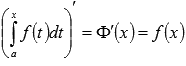 .
.
Действительно, запишем приращение функции 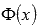 , соответствующее приращению аргумента
, соответствующее приращению аргумента 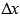 и воспользуемся пятым свойством определенного интеграла и следствием из десятого свойства:
и воспользуемся пятым свойством определенного интеграла и следствием из десятого свойства:
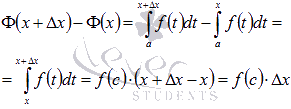
где 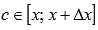 .
.
Перепишем это равенство в виде 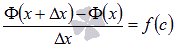 . Если вспомнить определение производной функции и перейти к пределу при
. Если вспомнить определение производной функции и перейти к пределу при 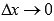 , то получим
, то получим 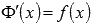 . То есть,
. То есть, 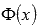 - это одна из первообразных функции y = f(x) на отрезке [a; b]. Таким образом, множество всех первообразных F(x) можно записать как
- это одна из первообразных функции y = f(x) на отрезке [a; b]. Таким образом, множество всех первообразных F(x) можно записать как 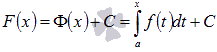 , где С – произвольная постоянная.
, где С – произвольная постоянная.
Вычислим F(a), используя первое свойство определенного интеграла: 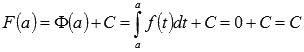 , следовательно,
, следовательно, 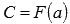 . Воспользуемся этим результатом при вычислении F(b):
. Воспользуемся этим результатом при вычислении F(b): 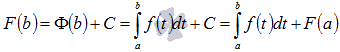 , то есть
, то есть 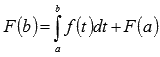 . Это равенство дает доказываемую формулу Ньютона-Лейбница
. Это равенство дает доказываемую формулу Ньютона-Лейбница 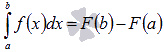 .
.
Приращение функции принято обозначать как 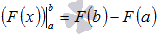 . Пользуясь этим обозначением, формула Ньютона-Лейбница примет вид
. Пользуясь этим обозначением, формула Ньютона-Лейбница примет вид 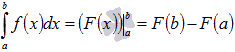 .
.
Выполнение упражнений
Итоги занятия
Домашнее задание
По учебнику «Алгебра и начала анализа» 10-11клас. А.Н. Колмогоров стр. 183-188
Тема: Применение интеграла (2ч)
Цель занятия:
расширение представлений у студентов о применении интеграла в
различных областях современной жизни
обобщение знаний по теме «Применение интеграла»;
Развитие коммуникационных компетенций при решении проблем творческого и поискового характера
развитие интеллектуальных способностей студентов;
Ход занятия
Пусть дано тело объемом V, причем имеется такая прямая, что для любой плоскости (рис. 125 стр. 194), перпендикулярной данной прямой, известна площадь сечения S тела этой плоскостью. Но плоскость перпендикулярная оси ОХ, пересекает ее в некоторой точке x. Следовательно, каждому числу x 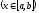 поставлено в соответствии единственное число
поставлено в соответствии единственное число 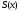 - площадь сечения тела этой плоскостью. Имеется функция
- площадь сечения тела этой плоскостью. Имеется функция 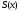 , заданная на отрезке
, заданная на отрезке  .
.
Если функция непрерывна на отрезке  , то справедлива формула
, то справедлива формула  .
.
Тело, полученное вращением криволинейной трапеции, ограниченной графиком непрерывной и неотрицательной на отрезке  функцией, отрезками прямых
функцией, отрезками прямых  и отрезком
и отрезком  оси ОХ, имеем объем, выражающийся по формуле:
оси ОХ, имеем объем, выражающийся по формуле:
 .
.
Действительно, каждая плоскость, перпендикулярная оси ОХ и пересекающая отрезок  этой оси в точке x, дает в сечении круг радиуса f(x). Соответственно, площадь сечения равна площади круга радиуса f(x):
этой оси в точке x, дает в сечении круг радиуса f(x). Соответственно, площадь сечения равна площади круга радиуса f(x):  .
.
На рисунке показан объем тела, полученного вращением криволинейной трапеции.
Выполнение упражнений
Итоги занятия
Домашнее задание
По учебнику «Алгебра и начала анализа» 10-11клас. А.Н. Колмогоров стр. 188-193








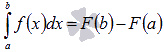 .
.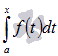 является функцией верхнего предела. Обозначим эту функцию
является функцией верхнего предела. Обозначим эту функцию 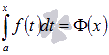 , причем эта функция непрерывная и справедливо равенство
, причем эта функция непрерывная и справедливо равенство 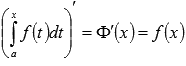 .
.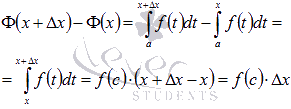
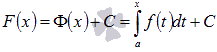 , где С – произвольная постоянная.
, где С – произвольная постоянная.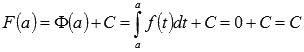 , следовательно,
, следовательно, 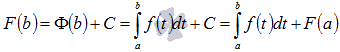 , то есть
, то есть 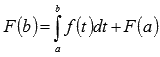 . Это равенство дает доказываемую формулу Ньютона-Лейбница
. Это равенство дает доказываемую формулу Ньютона-Лейбница 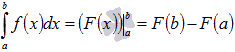 .
.









