ПЛАН УРОКА (2 курс)
УЧЕБНАЯ ДИСЦИПЛИНА МАТЕМАТИКА
КОЛИЧЕСТВО ЧАСОВ 1.
МЕСТО ПРОВЕДЕНИЯ КАБИНЕТ МАТЕМАТИКИ.
ТЕМА ЗАНЯТИЯ: Свойства функции. Экстремумы.
ЦЕЛИ ЗАНЯТИЯ:Образовательные Научить исследовать функцию на промежутки монотонности , находить экстремумы функции.
Развивающие: Развитие логическое мышление, устную и письменную культуру речи.
Воспитательные: Формировать навыки умственного труда – поиск рациональных путей выполнения работы.
Ожидаемые результаты освоения темы:
знать: признаки возрастания и убывания функции, алгоритм исследования функции на промежутки монотонности. Определения точек максимума и минимума функции; необходимое и достаточное условие существования экстремума, алгоритм исследования функции на экстремум.
уметь: исследовать несложные функции на промежутки монотонности, находить экстремумы функции.
Оснащение: Доска меловая, доска маркерная, плакат «основные функции и их графики».
Основные этапы занятия:
Организация начала занятия.
Приветствие.
Проверка отсутствующих.
Знакомство с темой урока, совместное целеполагание.
II. Разбор нового материала: Что будем изучать:
1. Введение.
2. Точки минимума и максимума.
3. Экстремум функции.
4. Примеры.
Введение в экстремумы функций
Ребята, давайте посмотрим на график некоторой функции: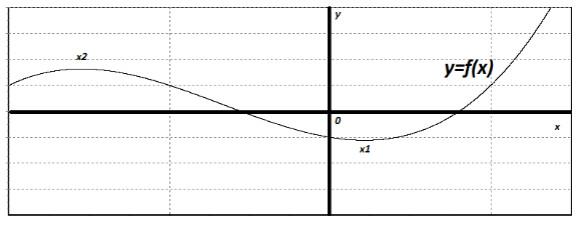
Заметит, что поведение нашей функции y=f (x) во многом определяется двумя точками x1 и x2. Давайте внимательно посмотрим на график функции в этих точках и около них. До точки x2 функция возрастает, в точке x2 происходит изгиб, и сразу после этой точки функция убывает до точки x1. В точке x1 функция опять изгибается, и после этого - опять возрастает. Точки x1 и x2 пока так и будем называть точками изгиба. Давайте проведем касательные в этих точках:
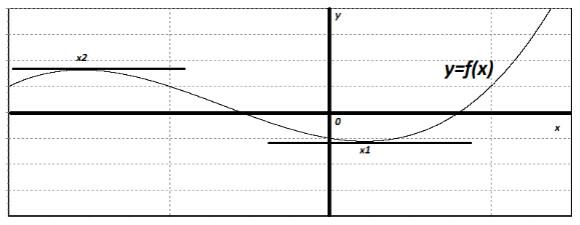
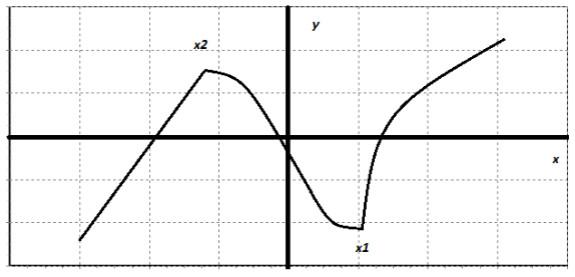
Точка x2 - это точка, в которой функция достигает наибольшего значения в некоторой области (рядом с точкой x2). Точка x1 - это точка, в которой функция достигает своего наименьшего значения в некоторой области (рядом с точкой x1).
Точки минимума и максимума
Определение: Точку x= x0 называют точкой минимума функции y=f(x), если существует окрестность точки x0, в которой выполняется неравенство: f(x) ≥ f(x0).
Определение: Точку x=x0 называют точкой максимума функции y=f(x), если существует окрестность точки x0, в которой выполняется неравенство: f(x) ≤ f(x0).
Ребята, а что такое окрестность?
Определение: Окрестность точки — множество точек, содержащее нашу точку, и близкие к ней.
Окрестность мы можем задавать сами. Например, для точки x=2, мы можем определить окрестность в виде точек 1 и 3.
Вернемся к нашим графикам, посмотрим на точку x2, она больше всех других точек из некоторой окрестности, тогда по определению - это точка максимума. Теперь посмотрим на точку x1, она меньше всех других точек из некоторой окрестности, тогда по определению - это точка минимума.
Ребята, давайте введем обозначения:
ymin - точка минимума,
ymax - точка максимума.
Важно! Ребята, не путайте точки максимума и минимума с наименьшим и наибольшим значение функции. Наименьшее и наибольшее значения ищутся на всей области определения заданной функции, а точки минимума и максимума в некоторой окрестности.
Экстремумы функции
Для точек минимума и максимума есть общей термин – точки экстремума.
Экстремум (лат. extremum – крайний) – максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума.
Соответственно, если достигается минимум – точка экстремума называется точкой минимума, а если максимум – точкой максимума.
III.Задачи для самостоятельного решения
а) Найти точки экстремума функции и определить их характер: y= 5x3 - 15x - 5.
б) Найти точки экстремума функции и определить их характер:

IV.Домашнее задание: К: г1, №78(а.б.в)
V.Рефлексия.




















