Площадь поверхности 5 кл Наглядная геометрия.

Упражнение 1

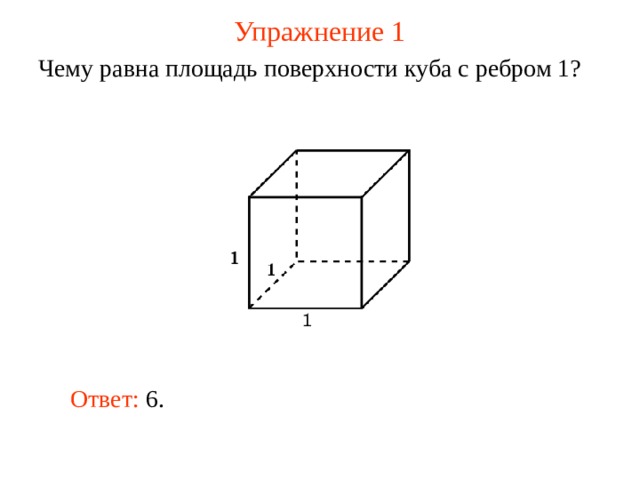
Чему равна площадь поверхности куба с ребром 1?

В режиме слайдов ответ появляется после кликанья мышкой

Ответ: 6.

Упражнение 2

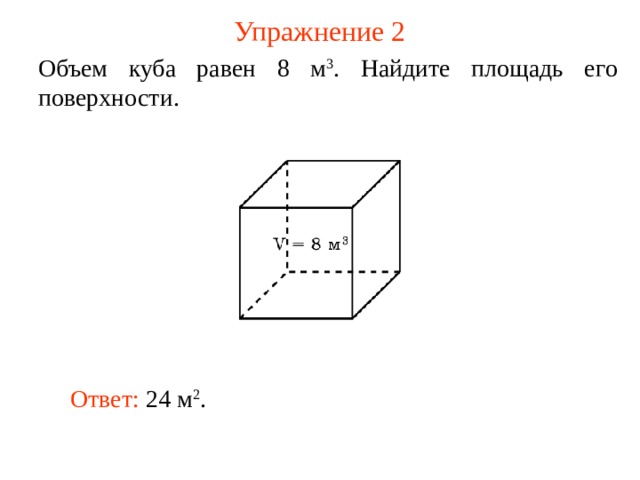
Объем куба равен 8 м 3 . Найдите площадь его поверхности.

В режиме слайдов ответ появляется после кликанья мышкой

Ответ: 24 м 2 .

Упражнение 3

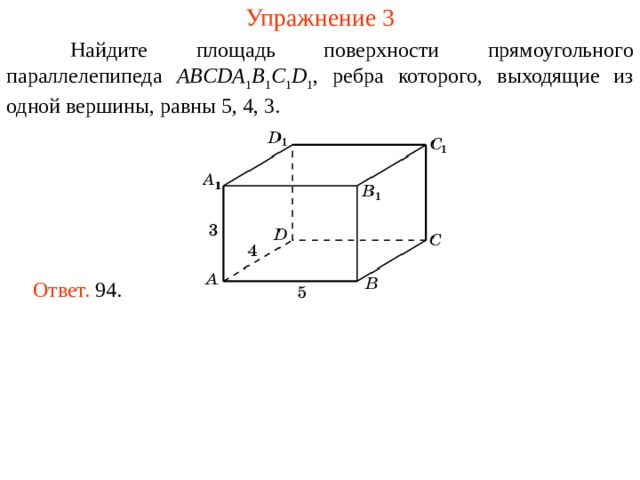
Найдите площадь поверхности прямоугольного параллелепипеда ABCDA 1 B 1 C 1 D 1 , ребра которого, выходящие из одной вершины, равны 5, 4, 3.

Ответ. 94 .

Упражнение 4

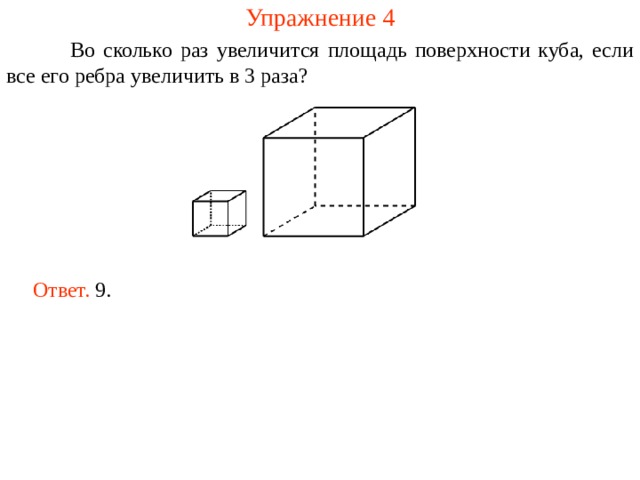
Во сколько раз увеличится площадь поверхности куба, если все его ребра увеличить в 3 раза?

Ответ. 9.

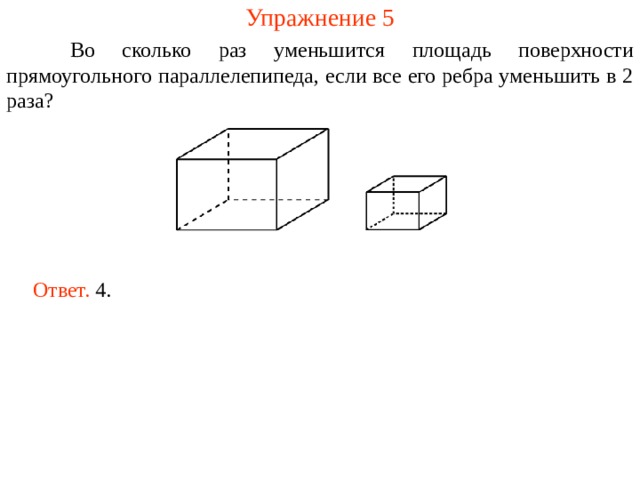
Упражнение 5

Во сколько раз уменьшится площадь поверхности прямоугольного параллелепипеда, если все его ребра уменьшить в 2 раза?

Ответ. 4.

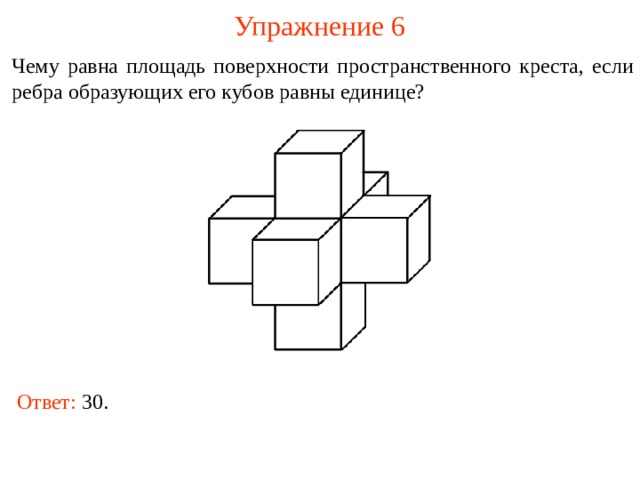
Упражнение 6

Чему рав на площадь поверхности пространственного креста, если ребра образующих его кубов равны единице?

В режиме слайдов ответы и решения появляются после кликанья мышкой

Ответ: 30 .

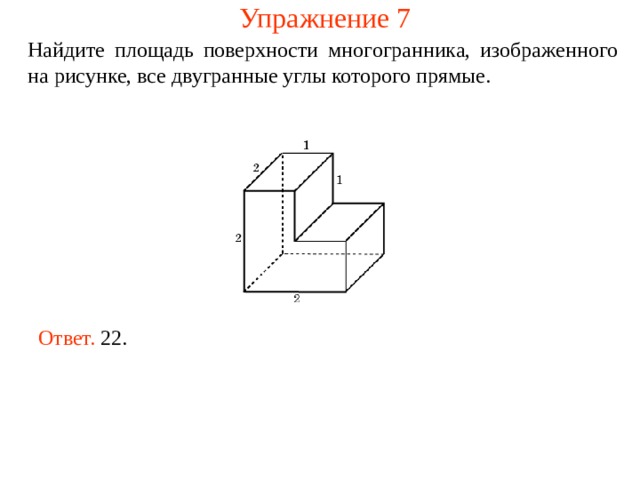
Упражнение 7

Найдите площадь поверхности многогранника, изображенного на рисунке, все двугранные углы которого прямые.

Ответ. 22.

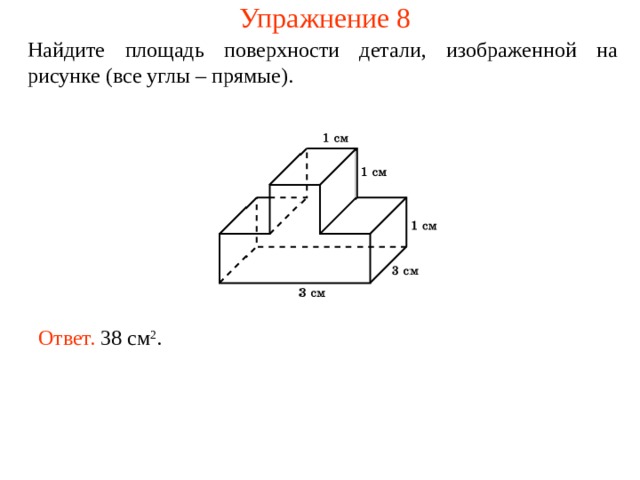
Упражнение 8

Найдите площадь поверхности детали, изображенной на рисунке (все углы – прямые). 

Ответ. 38 см 2 .

Упражнение 9

Найдите площадь поверхности многогранника, изображенного на рисунке, все двугранные углы которого прямые.

Ответ. 24.

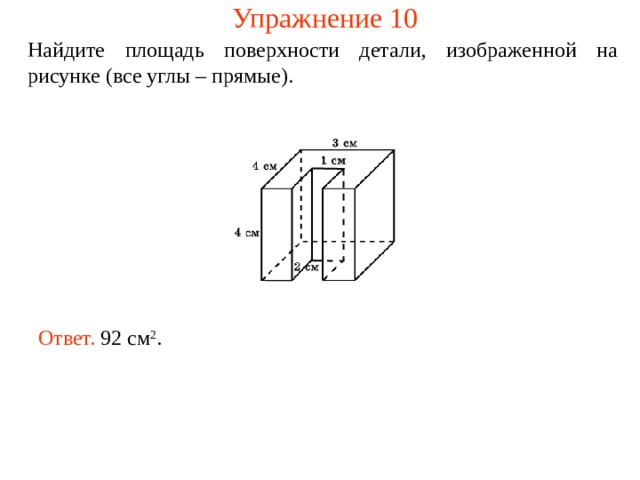
Упражнение 10

Найдите площадь поверхности детали, изображенной на рисунке (все углы – прямые). 

Ответ. 92 см 2 .

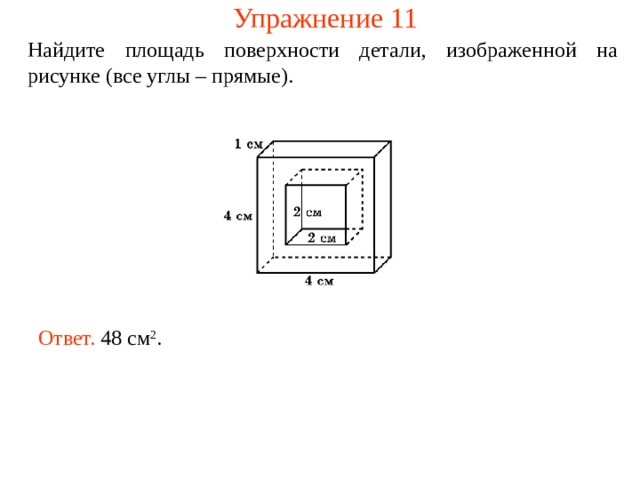
Упражнение 11

Найдите площадь поверхности детали, изображенной на рисунке (все углы – прямые). 

Ответ. 48 см 2 .

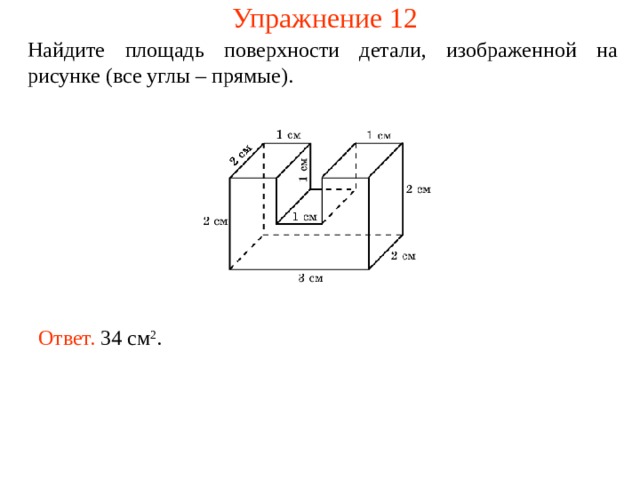
Упражнение 12

Найдите площадь поверхности детали, изображенной на рисунке (все углы – прямые). 

Ответ. 34 см 2 .

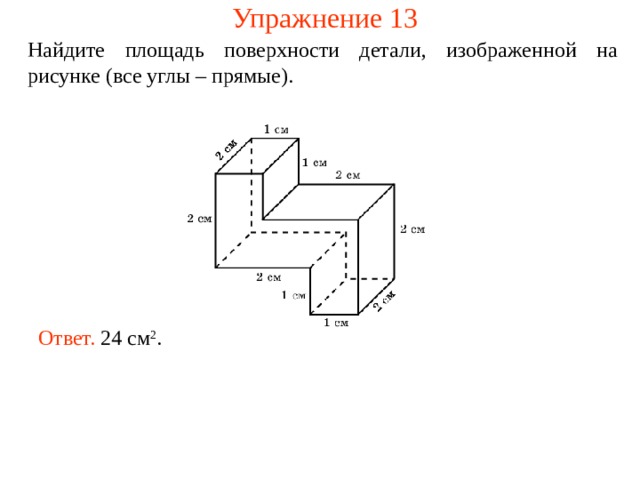
Упражнение 13

Найдите площадь поверхности детали, изображенной на рисунке (все углы – прямые). 

Ответ. 24 см 2 .

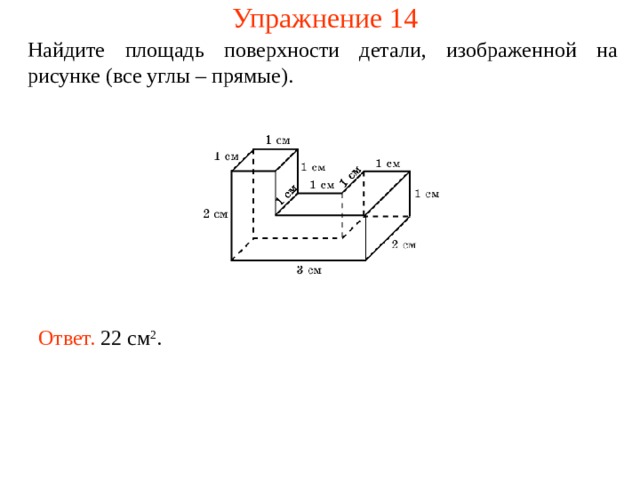
Упражнение 14

Найдите площадь поверхности детали, изображенной на рисунке (все углы – прямые). 

Ответ. 22 см 2 .

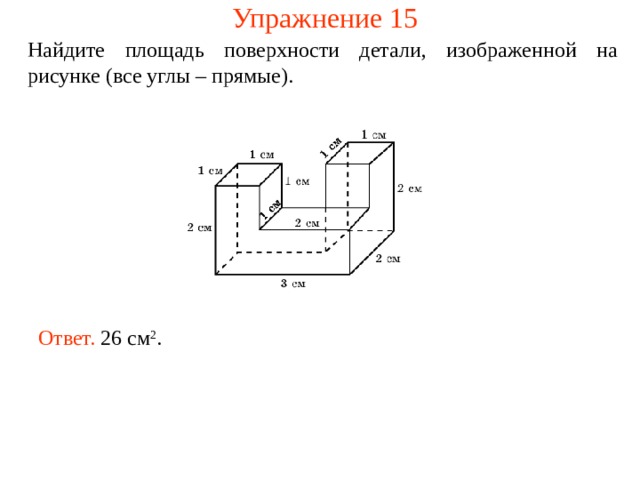
Упражнение 15

Найдите площадь поверхности детали, изображенной на рисунке (все углы – прямые). 

Ответ. 26 см 2 .

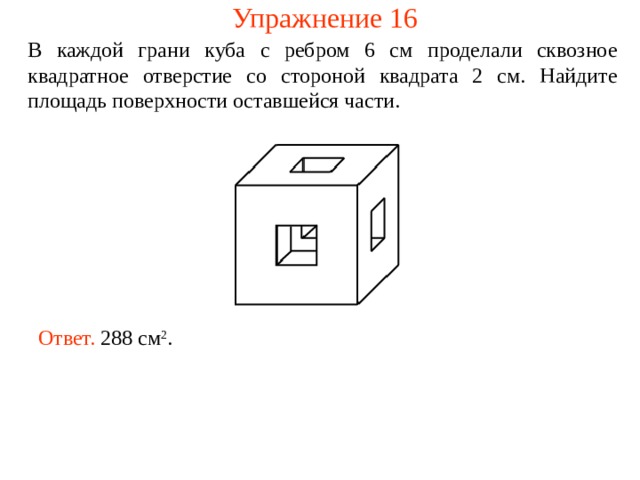
Упражнение 16

В каждой грани куба с ребром 6 см проделали сквозное квадратное отверстие со стороной квадрата 2 см. Найдите площадь поверхности оставшейся части.

Ответ. 288 см 2 .

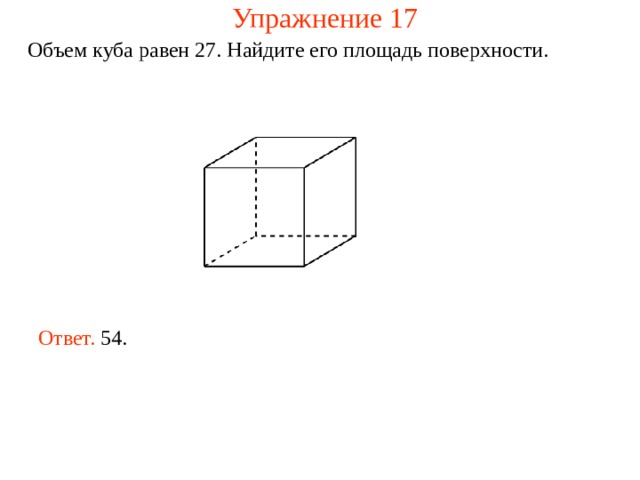
Упражнение 17

Объем куба равен 27. Найдите его площадь поверхности.

Ответ. 54.

Упражнение 18

Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2. Каким должно быть третье ребро, выходящее из той же вершины, чтобы площадь поверхности этого параллелепипеда равнялась 40?

Ответ. 4.

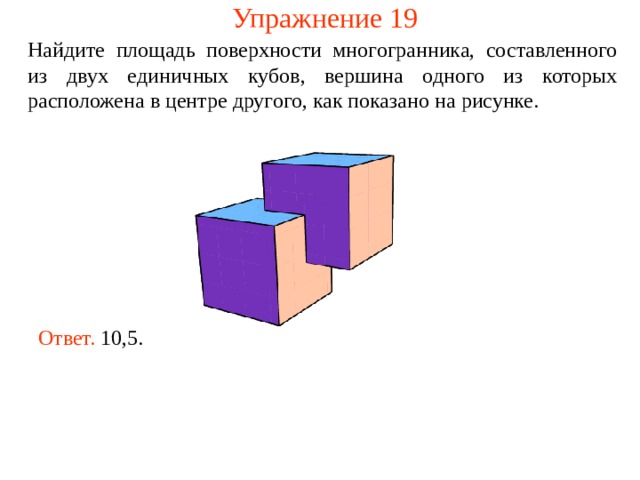
Упражнение 19

Найдите площадь поверхности многогранника, составленного из двух единичных кубов, вершина одного из которых расположена в центре другого, как показано на рисунке.

Ответ. 10,5.

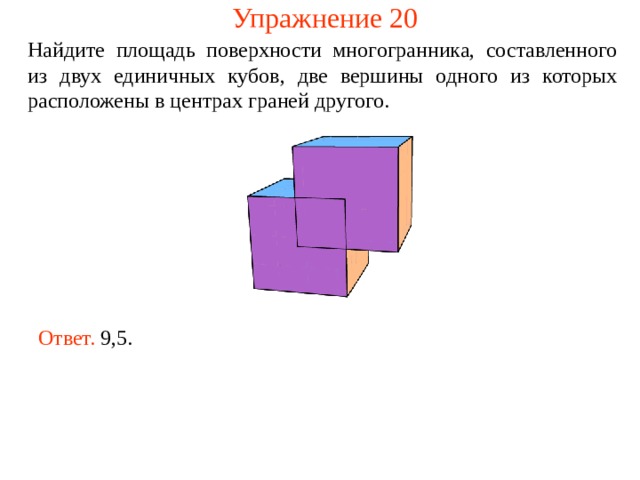
Упражнение 20

Найдите площадь поверхности многогранника, составленного из двух единичных кубов, две вершины одного из которых расположены в центрах граней другого.

Ответ. 9,5.