Подготовка к ЕГЭ. Рекурсивный алгоритм. Задание 16

Различные способы решения заданий ЕГЭ по информатике на примере задания 16: Рекурсивные алгоритмы.

Учитель Даташвили Любовь Отаровна МБОУ «Школа №66» г. Нижний Новгород

Алгоритм подготовки к ЕГЭ

Консультации с учителем

Открытый банк заданий ФИПИ

Проверить себя на пробном ЕГЭ, провести корректировку занятий

Информационный портал kompege

Тренажеры и симуляторы ЕГЭ по предмету

Подготовка к ЕГЭ на сайте

К. Полякова

Работа с печатными сборниками

Задания ЕГЭ по темам:

Тема

Номер задания

Системы счисления. Анализ числовых алгоритмов.

5, 8, 14

Кодирование информации.

4, 11

Графы. Матрица смежности.

1, 13

Поиск в тексте. Базы данных и электронные таблицы Excel

3, 9, 10, 18, 22

IP адреса. Маска сети.

13

Кодирование графической и звуковой информации. Комбинаторика

7, 8

Алгебра логики. Таблицы истинности. Исследование логических выражений.

2, 15

Циклические алгоритмы. Исполнители.

6, 12, 23

Теория игр

19 - 21

Рекурсия. Программирование

16, 17, 24, 25, 26, 27

Я выступаю за парадигму решения заданий несколькими способами, когда анализируются их достоинства и недостатки, возможные проблемы и «ловушки». Это позволяет выработке рекомендаций эффективных  методов решения  каждой конкретной задачи.

Задание №16

Впервые сталкиваясь с рекурсией, довольно значительное количество людей имеют проблемы с их пониманием.

По-своему определяют рекурсию математика, физика, программирование и ряд других научных дисциплин.

Рекурсивными  ситуациями, или  рекурсией   в  программировании, называют моменты, когда процедура или функция программы вызывает саму себя. Как бы странно для тех, кто начал изучать программирование, это ни звучало, здесь нет ничего странного. Следует запомнить, что  рекурсии  – это не сложно, и в отдельных случаях они заменяют циклы.

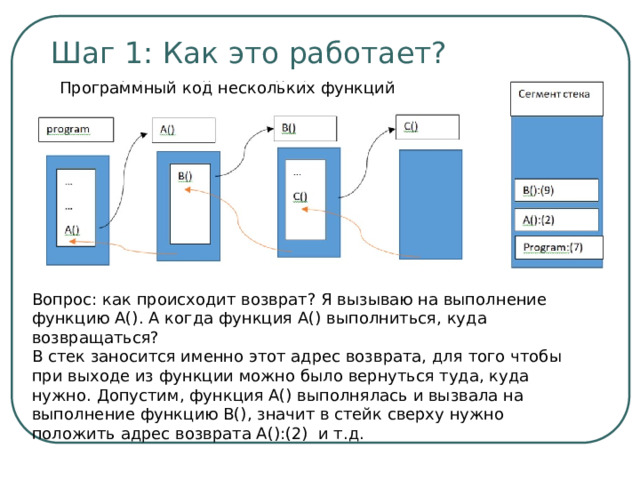
Шаг 1: Как это работает?

Программный код нескольких функций

Вопрос: как происходит возврат? Я вызываю на выполнение функцию А(). А когда функция А() выполниться, куда возвращаться?

В стек заносится именно этот адрес возврата, для того чтобы при выходе из функции можно было вернуться туда, куда нужно. Допустим, функция А() выполнялась и вызвала на выполнение функцию В(), значит в стейк сверху нужно положить адрес возврата A():(2) и т.д.

1: return f(n-1)+f(n-2) " width="640"

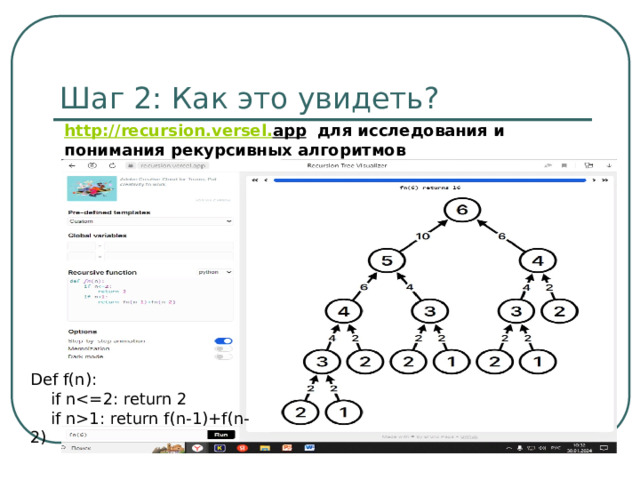
Шаг 2: Как это увидеть?

http :// recursion . versel . app для исследования и понимания рекурсивных алгоритмов

Def f(n):

if n

if n1: return f(n-1)+f(n-2)

Задание 4741

##4741 ответ 232

def F(n):

if (n**0.5).is_integer():

return int(n**0.5)

else:

return F(n+1)+1

print(F(4850)+F(5000))

2: ## return F(n-1)-2*F(n-2) return 1+F(n-1)+F(n-2) print (F(57)) " width="640"

Задание 4328. Использование декоратора @lru_cache(None)

##4328 ответ 1_096_305_888_485

Декоратор @lru_cache(None)

from functools import lru_cache

используют, если программа долго считает или происходит переполнение стека. Дело в том, что @lru_cache(None) сохраняет значения, которые были посчитаны, что позволяет не углубляться в рекурсию.

@lru_cache(None)

def F(n):

k=0

if n

if n2:

## return F(n-1)-2*F(n-2)

return 1+F(n-1)+F(n-2)

print (F(57))

=10000:return n if n return 1+F(n//2) if n return n**2+F(n+2) for i in range(9999,-1,-2): F(i) ##for i in range(10000,2): ## F(i) print(F(192)-F(9)) Если программа @lru_cache(None) не поможет, то здесь уже надо проанализировать задачу и сократить количество вычислений " width="640"

Задание 5160

##5160 ответ 89

from functools import lru_cache

@lru_cache(None)

def F(n):

if n=10000:return n

if n

return 1+F(n//2)

if n

return n**2+F(n+2)

for i in range(9999,-1,-2):

F(i)

##for i in range(10000,2):

## F(i)

print(F(192)-F(9))

Если программа @lru_cache(None) не поможет, то здесь уже надо проанализировать задачу и сократить количество вычислений

Или решить «руками» Задание 5160

Вывод:

Чтобы быть уверенным, что ты получишь балл за задание, нужно не просто запомнить и выучить структуру программы какого-то задания, а хорош разобраться в теме.