Подготовка к ЕГЭ задачи с экономическим содержанием "дифференцированные платежи"

Экономическая задача

Дифференцированный платеж

Задачи ЕГЭ №17 на кредиты обычно относятся к одному из двух характерных типов, которые легко различить между собой.

1 тип. Выплаты кредита производятся равными платежами. Это еще называется 

«аннуитет»

2 тип. Выплаты кредита подбираются так, что сумма долга уменьшается

равномерно. Это так называемая «схема с дифференцированными платежами».

К первому типу относятся также задачи, в которых есть информация о платежах.

Ко второму типу — задачи, в которых есть информация об изменении суммы долга.

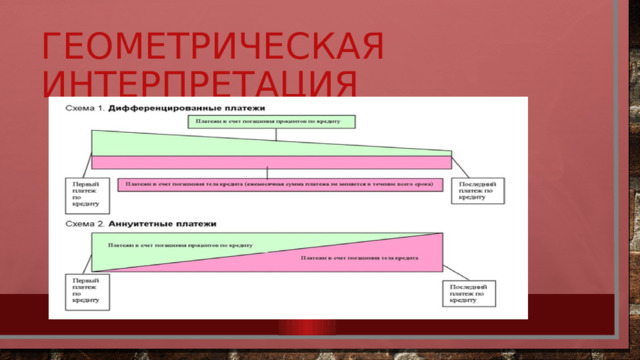
Геометрическая интерпретация

Схема с дифференцированными платежами

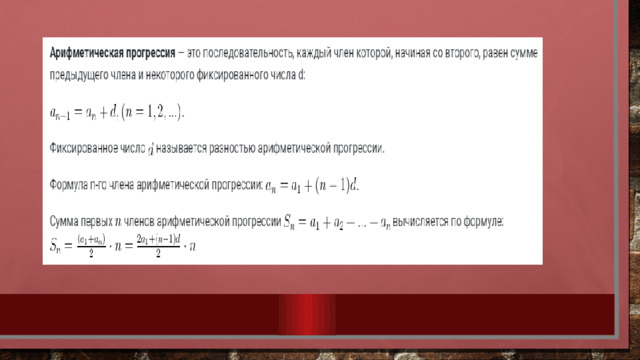
Разберем задачи

1. 15-го января планируется взять кредит в банке на 19 месяцев. Условия его возврата таковы:

— 1-го числа каждого месяца долг возрастёт на r\% по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца. Известно, что общая сумма выплат после полного погашения кредита на 30\% больше суммы, взятой в кредит. Найдите r.

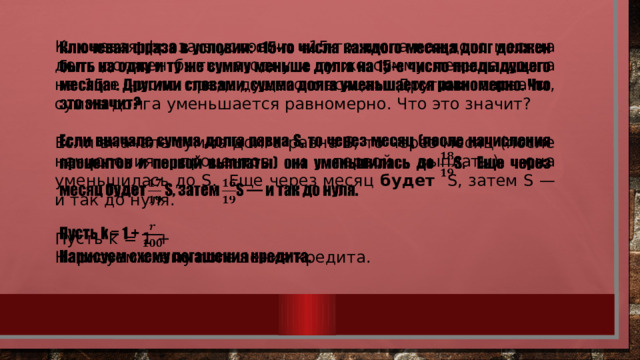
Ключевая фраза в условии: «15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца». Другими словами, сумма долга уменьшается равномерно. Что это значит?

Если вначале сумма долга равна S, то через месяц (после начисления процентов и первой выплаты) она уменьшилась до S. Еще через месяц будет S, затем S — и так до нуля.

Пусть k = 1 +

Нарисуем схему погашения кредита.

Схема погашения кредита

Первая строка в схеме — сумма долга после очередной выплаты.

Вторая строка — сумма долга после начисления процентов. Стрелками показано, как меняется сумма долга. Число платежных периодов n = 19.

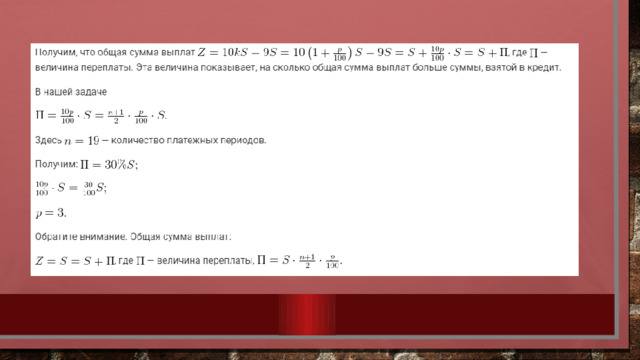
Попробуем разобраться. рассмотрим общую схему

N, или количество выплат

N, или количество выплат

Долг после начисления прооцентов (I проценты- i=,)

1

1

Выплата основная и % (т.е.часть кредита и начисленные проценты)

Выплата основная и % (т.е.часть кредита и начисленные проценты)

2

S(i + 1) = Si + S

S(i + 1) = Si + S

2

Долг после выплаты

Долг после выплаты

+ Si

3

S(i + 1) = Sr + S

3

…… .

…… .

Si+S-Si- =S- = S

S(i+ 1) = Si + S

+ S

…

n

n

+ S

…

S = S

сумма

S(i + 1) = S + S

…

S

…

сумма

+ S

…

…

S + X= S+Si+Si + +….+Si

0

0

S + Si

Разберем задачу: Банк предлагает клиентам кредит на 1 млн рублей на следующих условиях: – каждый год банк начисляет на оставшуюся часть долга 10%; – после начисления процентов клиент обязан внести платеж; – через 5 лет кредит должен быть выплачен полностью; – система выплат дифференцированная.

• Сколько процентов от первоначального долга составит переплата по такому кредиту?   Т.к. кредит выдается на 5 лет, это значит, что долг должен уменьшаться каждый год на ⋅1 млн рублей, то есть после первой выплаты долг составит 1−⋅1= млн рублей, после второй −= млн рублей и т.д.  
• Составим таблицу, причем все вычисления будем производить в млн рублей:

Решим задачу

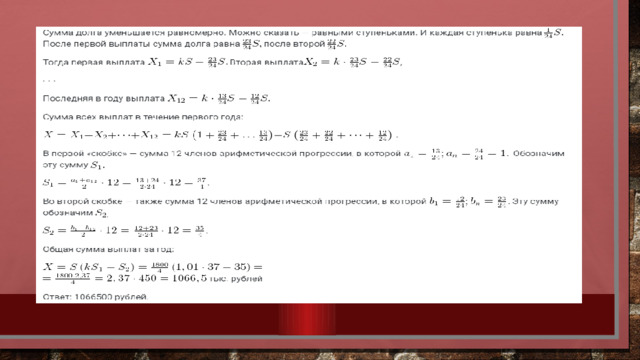
2. Жанна взяла в банке в кредит 1,8 млн рублей на срок 24 месяца. По договору Жанна должна возвращать банку часть денег в конце каждого месяца. Каждый месяц общая сумма долга возрастает на 1 %, а затем уменьшается на сумму, уплаченную Жанной банку в конце месяца. Суммы, выплачиваемые Жанной, подбираются так, чтобы сумма долга уменьшалась равномерно, то есть на одну и ту же величину каждый месяц. Какую сумму Жанна вернёт банку в течение первого года кредитования?

В этой задаче сумма долга уменьшается равномерно — задача второго типа. Пусть S — первоначальная сумма долга, S = 1800 тысяч рублей. Нарисуем схему начисления процентов и выплат. И заметим некоторые закономерности. Как обычно, k= 1 +

3. 15-го января был выдан полугодовой кредит на развитие бизнеса. В таблице представлен график его погашения.

Дата 15,01 15,02 15,03 15,04 15,05 15,06 15,07

Долг (в процентах от кредита) 100% 90% 80% 70% 60% 50% 0%

В конце каждого месяца, начиная с января, текущий долг увеличивался на 5\%, а выплаты по погашению кредита происходили в первой половине каждого месяца, начиная с февраля. На сколько процентов общая сумма выплат при таких условиях больше суммы самого кредита?

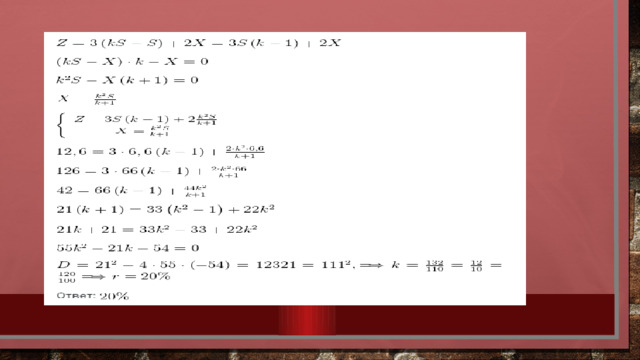
4. В июле 2016 года планируется взять кредит в размере 6,6 млн. руб. Условия возврата таковы:

- каждый январь долг возрастает на r\% по сравнению с концом предыдущего года.

- с февраля по июнь необходимо выплатить часть долга.

- в июле 2017, 2018 и 2019 годов долг остается равным 6,6 млн. руб.

- суммы выплат 2020 и 2021 годов равны.

Найдите r, если в 2021 году долг будет выплачен полностью и общие выплаты составят 12,6 млн. рублей.

В истории черпаем мы мудрость, в поэзии – остроумие, в математике - проницательность

Роджер Бэкон

Спасибо за внимание