Подготовка к ГВЭ-9 по математике( 6 задание)

Трапеция

Задание с 27.04 по 30.04.

1 часть

• Записать понятие трапеции и ее свойство.
• Записать виды трапеции и их свойства.
• Записать определения средней линии трапеции, чему она равна.
• Записать формулу площади трапеции

2 часть

Решить задачи (только те, на которых указано, что их ответ надо записать в тетрадь)

Вспомним!!!!!

• Сумма углов в треугольнике равна 180°.
• Сумма углов в четырехугольнике равна 360°.

Свойства углов при параллельных прямых

∠ 1= ∠ 6 (как накрестлежащие)

Прямые a ǁb, с-секущая

∠ 2= ∠5 (как накрестлежащие)

∠ 1= ∠3 (как соответственные)

∠ 2= ∠4 (как соответственные)

∠ 8= ∠6 (как соответственные)

∠ 5= ∠7 (как соответственные)

∠ 1= ∠8 (как вертикальные)

∠ 2= ∠7 (как вертикальные)

∠ 3= ∠6 (как вертикальные)

∠ 4= ∠5 (как вертикальные)

∠ 1+ ∠5=180°

∠ 2+ ∠6=180°

4

3

a

5

6

1

2

8

7

b

c

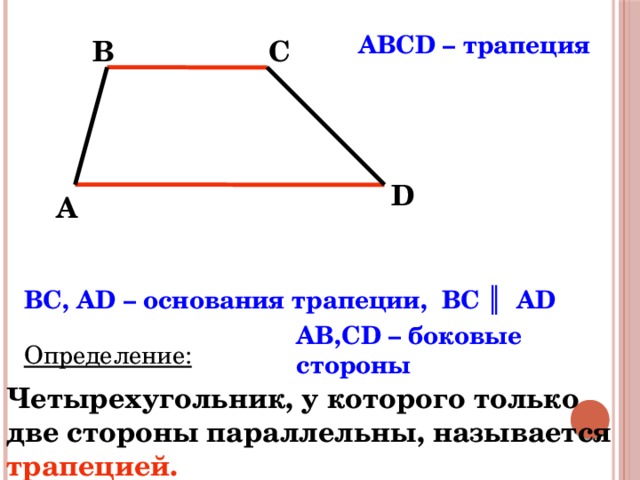
ABCD – трапеция

B

C

D

A

BC, AD – основания трапеции, ВС ║ АD

AB,CD – боковые стороны

Определение:

Четырехугольник, у которого только две стороны параллельны, называется трапецией.

Трапеция в жизни

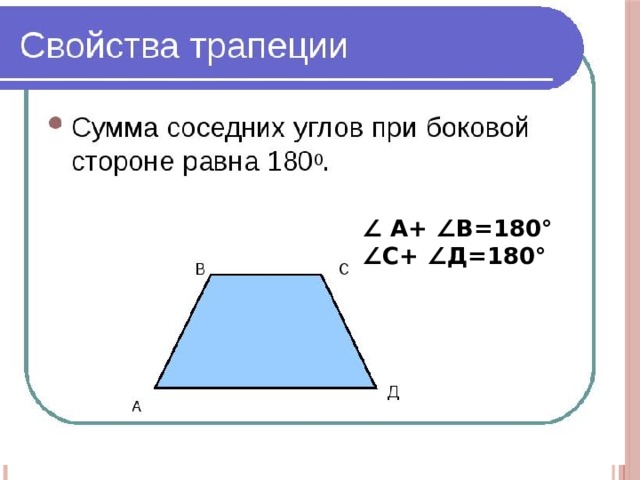
∠ A+ ∠B=180°

∠ C+ ∠Д=180°

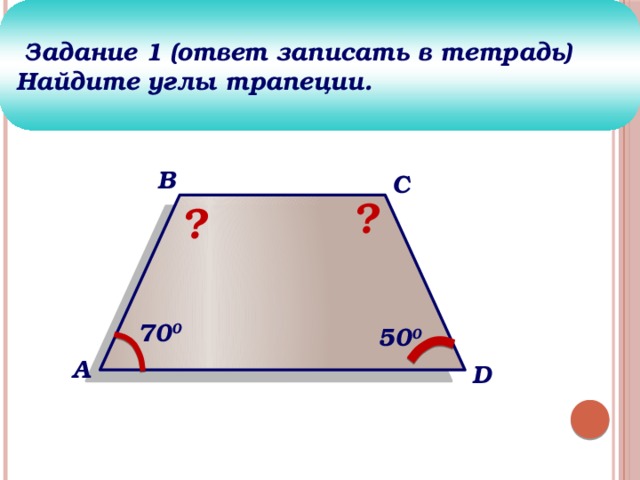
Задание 1 (ответ записать в тетрадь)

Найдите углы трапеции.

В

С

?

?

70 0

50 0

А

D

4

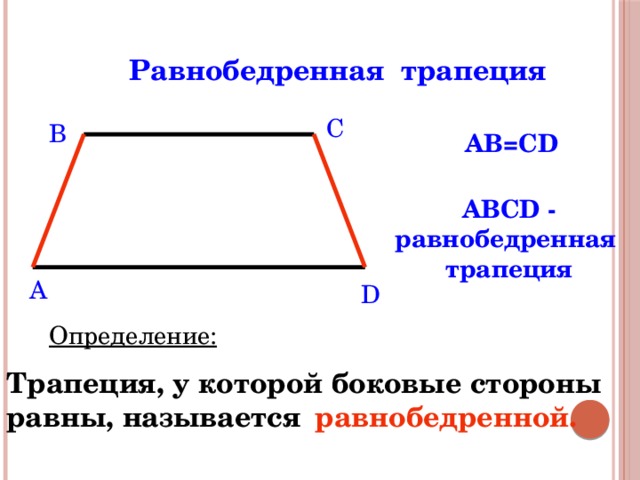
Равнобедренная трапеция

C

B

AB=CD

ABCD - равнобедренная трапеция

A

D

Определение:

Трапеция, у которой боковые стороны равны, называется равнобедренной.

Свойства углов равнобедренной трапеции

B

C

∠

А

D

А

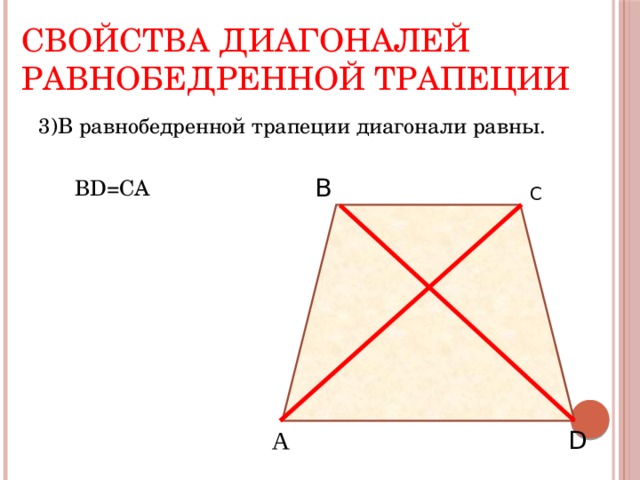
Свойства диагоналей равнобедренной трапеции

3)В равнобедренной трапеции диагонали равны.

BD=CA

B

C

D

Задачи

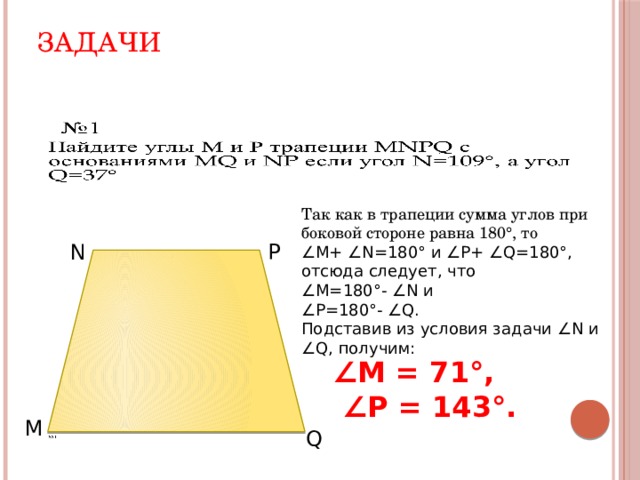
Так как в трапеции сумма углов при боковой стороне равна 180°, то

∠ M+ ∠N=180° и ∠P+ ∠Q=180°, отсюда следует, что

∠ М=180°- ∠N и

∠ Р=180°- ∠Q.

Подставив из условия задачи ∠N и ∠Q, получим:

N

P

∠ M = 71 °,

∠ P = 143 °.

M

Q

Задачи

Так как углы при основании в равнобедренной трапеции равны, то

∠ A= ∠D.

Сумма углов при боковой стороне равна 180°, то ∠B=180°- ∠A, ∠C=180°- ∠D.

Пусть ∠А=115°, следовательно, ∠D=115°,

∠ В=180°-115°=65° и аналогично ∠С=65°

B

C

Ответ: 115 °, 65°,65°

D

A

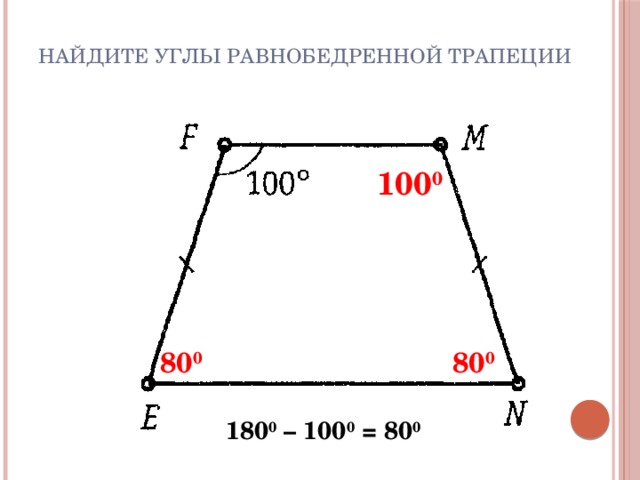
Найдите углы равнобедренной трапеции

100 0

80 0

80 0

180 0 – 100 0 = 80 0

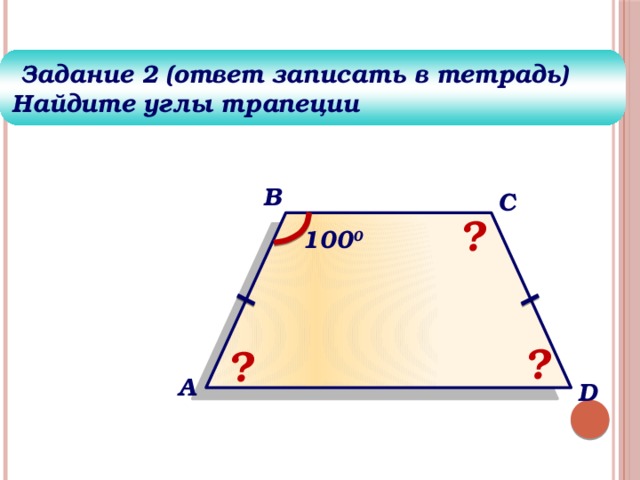
Задание 2 (ответ записать в тетрадь)

Найдите углы трапеции

В

С

?

100 0

?

?

А

D

8

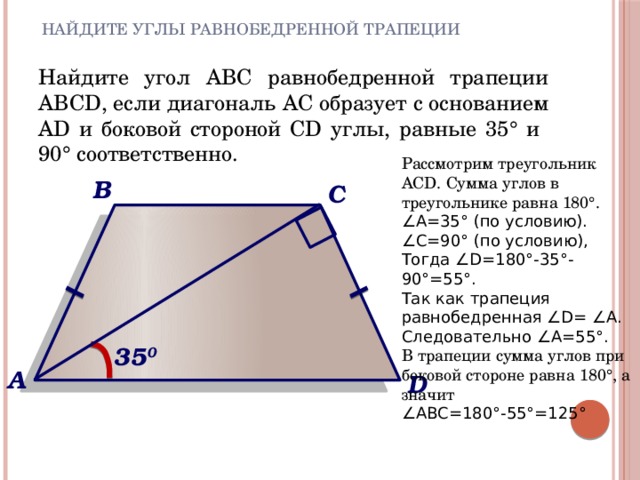
Найдите углы равнобедренной трапеции

Найдите угол ABC равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной CD углы, равные 35° и 90° соответственно.

Рассмотрим треугольник ACD. Сумма углов в треугольнике равна 180°.

∠ А=35° (по условию).

∠ С=90° (по условию),

Тогда ∠D=180°-35°-90°=55°.

Так как трапеция равнобедренная ∠D= ∠A. Следовательно ∠А=55°.

В трапеции сумма углов при боковой стороне равна 180°, а значит

∠ АВС=180°-55°=125°

В

С

35 0

А

D

8

Задание для решения в тетради

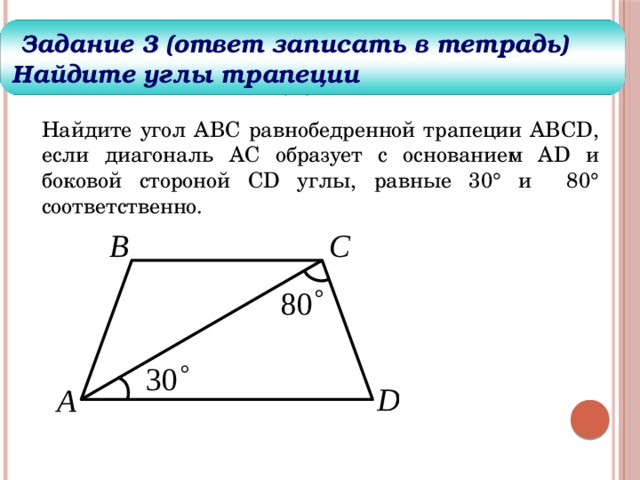
Задание 3 (ответ записать в тетрадь)

Найдите углы трапеции

Найдите угол ABC равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной CD углы, равные 30° и 80° соответственно.

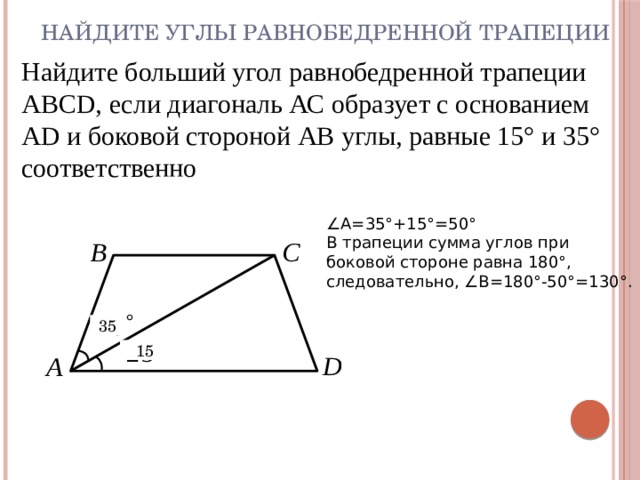
Найдите углы равнобедренной трапеции

Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 15° и 35° соответственно

∠ А=35°+15°=50°

В трапеции сумма углов при боковой стороне равна 180°, следовательно, ∠В=180°-50°=130°.

35

15

8

Задание для решения

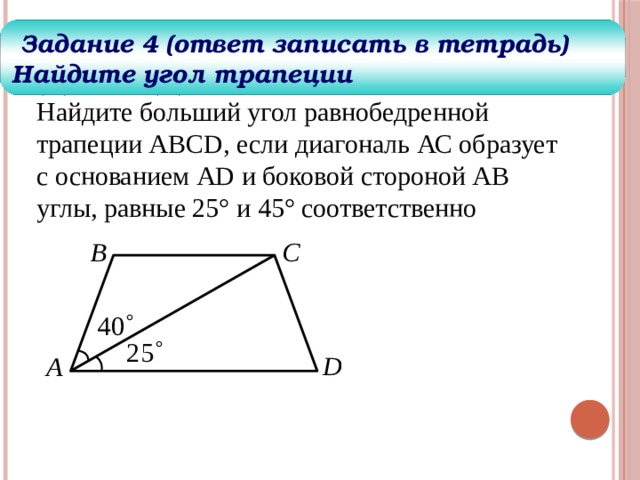
Задание 4 (ответ записать в тетрадь)

Найдите угол трапеции

Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 25° и 45° соответственно

8

Найдите углы равнобедренной трапеции

Сумма двух углов равнобедренной трапеции равна 150º. Найдите больший угол трапеции. Ответ дайте в градусах.

Решение:

Так как трапеция равнобедренная, то у нее равны углы при основании, следовательно, каждый из этих углов равен 150°:2=75°.

Мы знаем о том, что сумма углов при боковой стороне в трапеции равна 180°, а значит, больший угол равен

180°-75°=105°

Задания для решения

Задание 5 (ответ записать в тетрадь)

Найдите угол трапеции

Сумма двух углов равнобедренной трапеции равна 178º. Найдите больший угол трапеции. Ответ дайте в градусах. Ответ: ___________________________

Задания для решения

Задание 6 (ответ записать в тетрадь)

Найдите угол трапеции

В трапеции средняя линия равна 12, меньшее основание 5. Найдите длину большего основания.

Ответ_______________

Задания для решения

Задание 7 (ответ записать в тетрадь)

Найдите угол трапеции

Сумма двух углов равнобедренной трапеции равна 222°. Найдите меньший угол этой трапеции. Ответ дайте в градусах.

Задания для решения

Задание 8 (ответ записать в тетрадь)

Найдите угол трапеции

Сумма двух углов равнобедренной трапеции равна 294°. Найдите меньший угол этой трапеции. Ответ дайте в градусах.

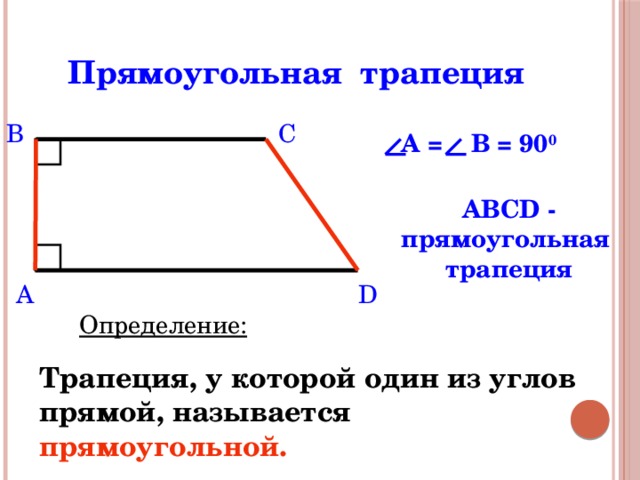
Прямоугольная трапеция

B

C

A = В = 90 0

ABCD - прямоугольная трапеция

D

A

Определение:

Трапеция, у которой один из углов прямой, называется прямоугольной.

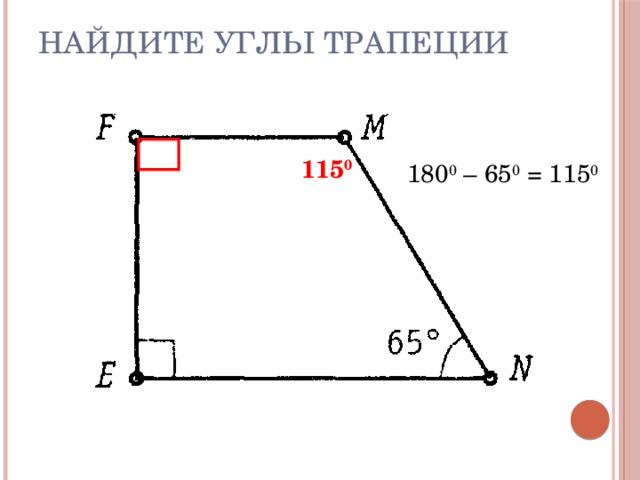
Найдите углы трапеции

115 0

180 0 – 65 0 = 115 0

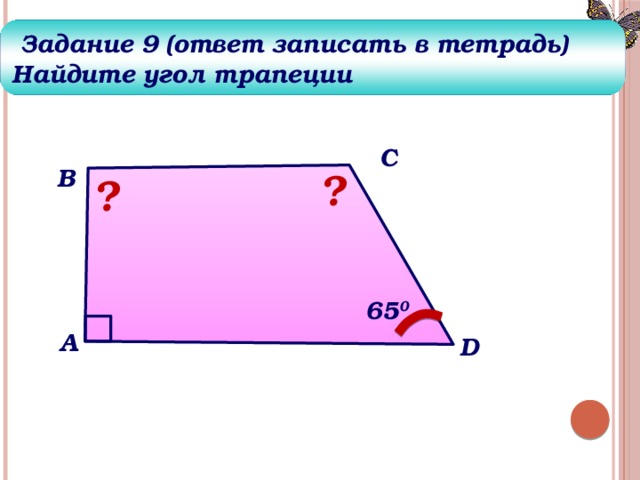
Задание 9 (ответ записать в тетрадь)

Найдите угол трапеции

С

В

?

?

65 0

А

D

24

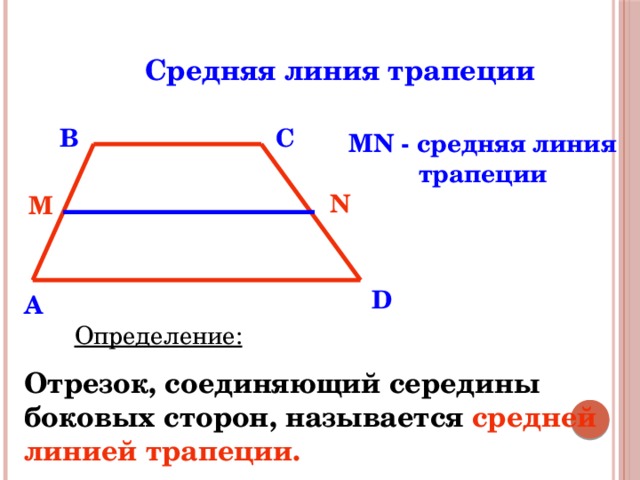
Средняя линия трапеции

B

C

MN - средняя линия трапеции

N

M

D

A

Определение:

Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.

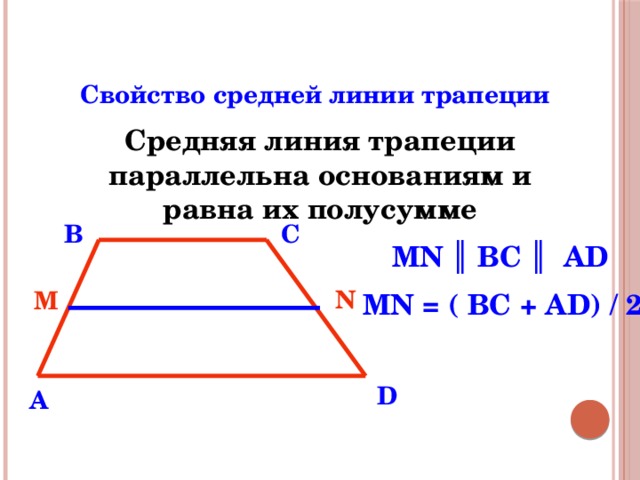
Свойство средней линии трапеции

Средняя линия трапеции параллельна основаниям и равна их полусумме

B

C

MN ║ ВС ║ АD

MN = ( BC + AD) / 2

N

M

D

A

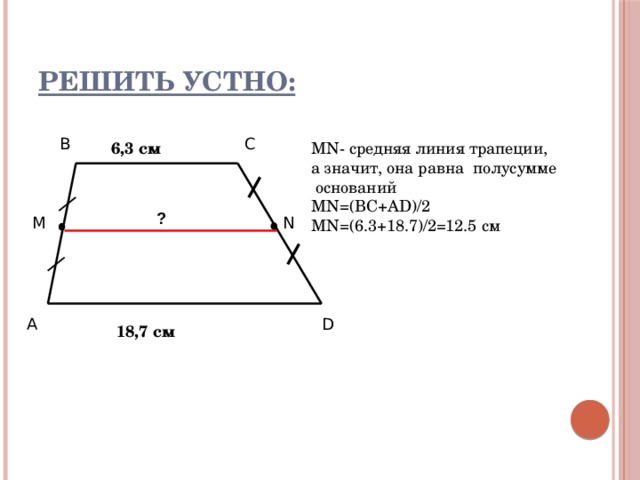
Решить устно:

B

C

6,3 см

MN- средняя линия трапеции,

а значит, она равна полусумме

оснований

MN=(BC+AD)/2

MN=(6.3+18.7)/2=12.5 см

?

N

M

A

D

18,7 см

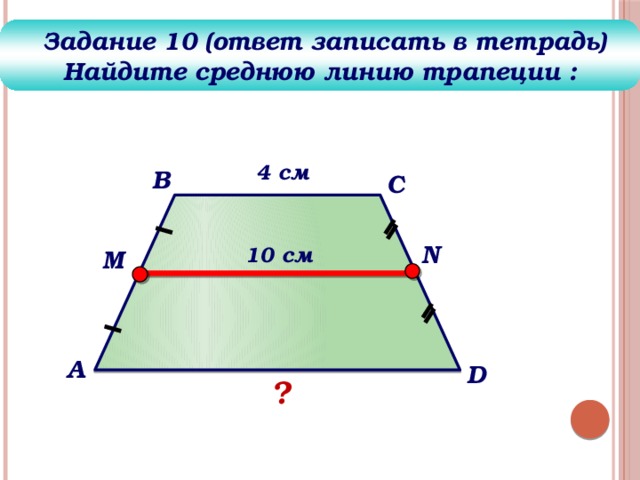
Задание 10 (ответ записать в тетрадь)

Найдите среднюю линию трапеции :

4 см

В

С

N

10 см

М

А

D

?

29

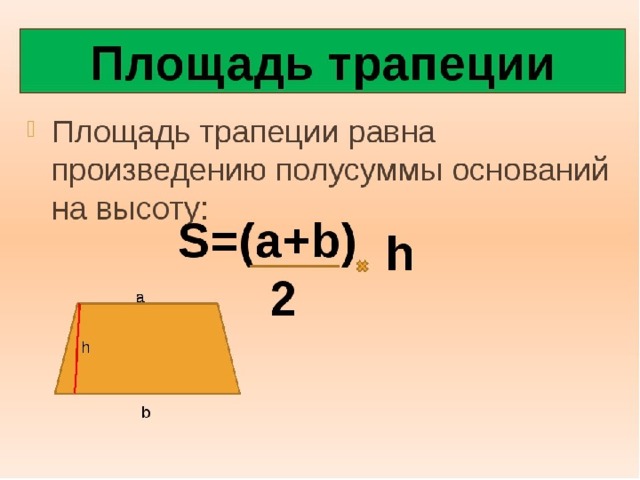
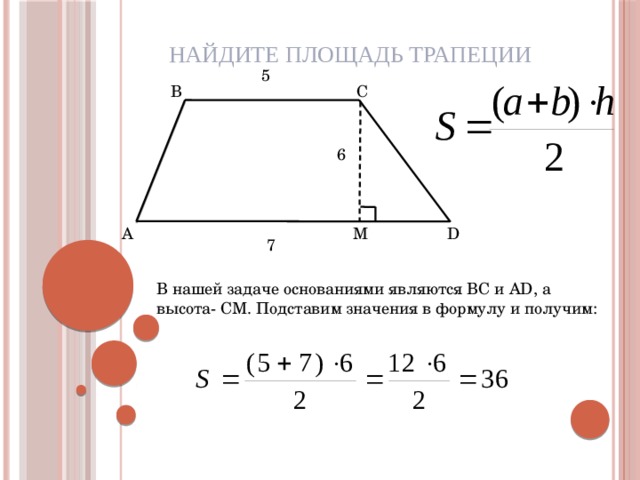
Найдите площадь трапеции

5

В

С

6

D

M

А

7

В нашей задаче основаниями являются BC и AD, а высота- СМ. Подставим значения в формулу и получим:

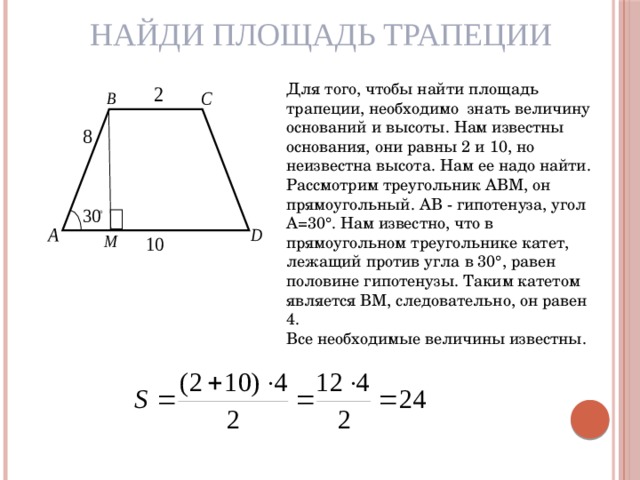
Найди площадь трапеции

Для того, чтобы найти площадь трапеции, необходимо знать величину оснований и высоты. Нам известны основания, они равны 2 и 10, но неизвестна высота. Нам ее надо найти.

Рассмотрим треугольник АВМ, он прямоугольный. АВ - гипотенуза, угол А=30°. Нам известно, что в прямоугольном треугольнике катет, лежащий против угла в 30°, равен половине гипотенузы. Таким катетом является ВМ, следовательно, он равен 4.

Все необходимые величины известны.

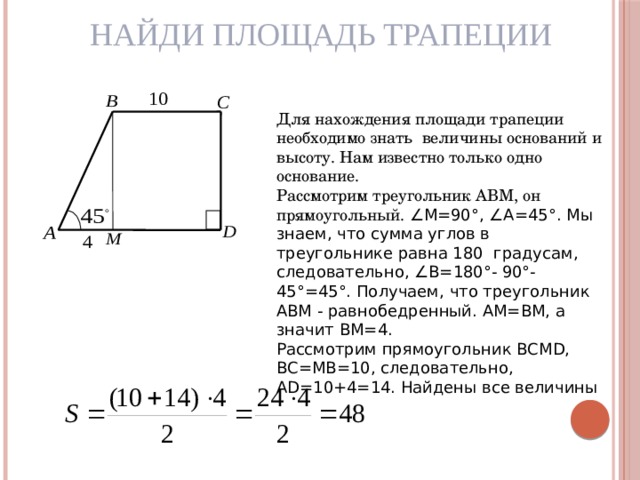
Найди площадь трапеции

Для нахождения площади трапеции необходимо знать величины оснований и высоту. Нам известно только одно основание.

Рассмотрим треугольник АВМ, он прямоугольный. ∠М=90°, ∠А=45°. Мы знаем, что сумма углов в треугольнике равна 180 градусам, следовательно, ∠В=180°- 90°-45°=45°. Получаем, что треугольник АВМ - равнобедренный. АМ=ВМ, а значит ВМ=4.

Рассмотрим прямоугольник BCMD, ВС=МВ=10, следовательно, AD=10+4=14. Найдены все величины

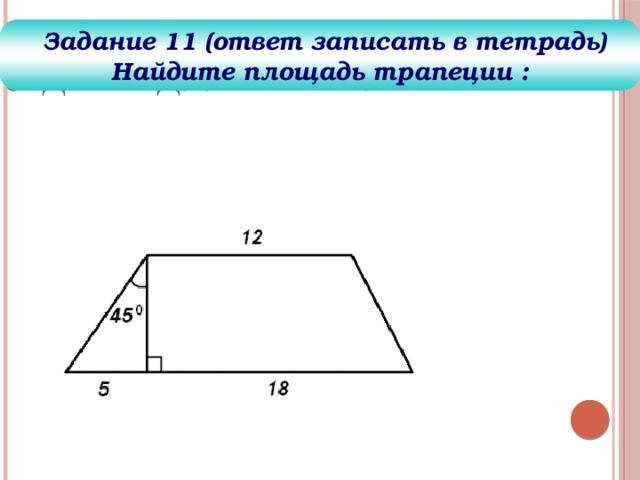
Задание для решения

Задание 11 (ответ записать в тетрадь)

Найдите площадь трапеции :