Подготовка к ОГЭ по математике 2023

Подготовка к ОГЭ

Иксанова Елена Геннадьевна

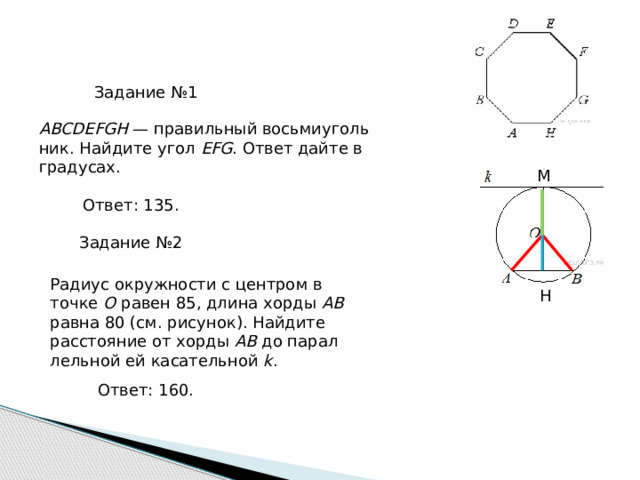
Задание №1

ABCDEFGH — пра­виль­ный вось­ми­уголь­ник. Най­ди­те угол EFG . Ответ дайте в гра­ду­сах.

M

Ответ: 135.

Задание №2

Ра­ди­ус окруж­но­сти с цен­тром в точке O равен 85, длина хорды AB равна 80 (см. ри­су­нок). Най­ди­те рас­сто­я­ние от хорды AB до па­рал­лель­ной ей ка­са­тель­ной k .

H

Ответ: 160.

Ра­ди­ус окруж­но­сти с цен­тром в точке O равен 85, длина хорды AB равна 102 (см. ри­су­нок). Най­ди­те рас­сто­я­ние от хорды AB до па­рал­лель­ной ей ка­са­тель­ной k .

Ответ: 153.

Задание 3

ABCDEFGH - пра­виль­ный вось­ми­уголь­ник. Най­ди­те угол . Ответ дайте в гра­ду­сах.

Ответ: 22,5.

Задание№4

Задания 19

Ука­жи­те но­ме­ра вер­ных утвер­жде­ний.

• 1) Если при пе­ре­се­че­нии двух пря­мых тре­тьей пря­мой со­от­вет­ствен­ные углы равны 65°, то эти две пря­мые па­рал­лель­ны.
• 2) Любые две пря­мые имеют не менее одной общей точки.
• 3) Через любую точку про­хо­дит более одной пря­мой.
• 4) Любые три пря­мые имеют не менее одной общей точки.

• 1) Если при пе­ре­се­че­нии двух пря­мых тре­тьей пря­мой внут­рен­ние на­крест ле­жа­щие углы со­став­ля­ют в сумме 90°, то эти две пря­мые па­рал­лель­ны.

• 2) Если угол равен 60°, то смеж­ный с ним равен 120°.

• 3) Если при пе­ре­се­че­нии двух пря­мых тре­тьей пря­мой внут­рен­ние од­но­сто­рон­ние углы равны 70° и 110°, то эти две пря­мые па­рал­лель­ны.

• 4) Через любые три точки про­хо­дит не более одной пря­мой.

Ответ: 13.

Ответ: 234.

К окруж­но­сти с цен­тром в точке O про­ве­де­ны ка­са­тель­ная AB и се­ку­щая AO . Най­ди­те ра­ди­ус окруж­но­сти, если AB=32, AO=40 .

Задания 16

Задание №5

На от­рез­ке AB вы­бра­на точка Cтак, что AC=10 и BC=16 . По­стро­е­на окруж­ность с цен­тром A , про­хо­дя­щая через C . Най­ди­те длину от­рез­ка ка­са­тель­ной, про­ведённой из точкиB к этой окруж­но­сти.

Ответ: 24.

H

Задание №6

Ответ: 24.

Задание №7

От­ре­зок AB=72 ка­са­ет­ся окруж­но­сти ра­ди­у­са 54 с цен­тром O в точке B . Окруж­ность пе­ре­се­ка­ет от­ре­зок AO в точке D . Най­ди­те AD.

Ответ: 36.

Задание №8

Пря­мая ка­са­ет­ся окруж­но­сти в точке K . Точка O — центр окруж­но­сти. Хорда KM об­ра­зу­ет с ка­са­тель­ной угол, рав­ный 83°. Най­ди­те ве­ли­чи­ну угла OMK . Ответ дайте в гра­ду­сах.

Ответ: 7.

Ука­жи­те но­ме­ра вер­ных утвер­жде­ний.

•   1) Если три сто­ро­ны од­но­го тре­уголь­ни­ка про­пор­ци­о­наль­ны трём сто­ро­нам дру­го­го тре­уголь­ни­ка, то тре­уголь­ни­ки по­доб­ны.
• 2) Сумма смеж­ных углов равна 180°.
• 3) Любая вы­со­та рав­но­бед­рен­но­го тре­уголь­ни­ка яв­ля­ет­ся его бис­сек­три­сой.

• 1) Если угол равен 45°, то вер­ти­каль­ный с ним угол равен 45°.
• 2) Любые две пря­мые имеют ровно одну общую точку.
• 3) Через любые три точки про­хо­дит ровно одна пря­мая.
• 4) Если рас­сто­я­ние от точки до пря­мой мень­ше 1, то и длина любой на­клон­ной, про­ве­ден­ной из дан­ной точки к пря­мой, мень­ше 1.
•  

Ответ: 12. 

Ответ: 1.

Задание№1

Фирма «Вспыш­ка» из­го­тав­ли­ва­ет фо­на­ри­ки. Ве­ро­ят­ность того, что слу­чай­но вы­бран­ный фо­на­рик из пар­тии бра­ко­ван­ный, равна 0,02. Ка­ко­ва ве­ро­ят­ность того, что два слу­чай­но вы­бран­ных из одной пар­тии фо­на­ри­ка ока­жут­ся не­бра­ко­ван­ны­ми?

Ре­ше­ние. Ве­ро­ят­ность того, что один слу­чай­но вы­бран­ный из пар­тии фо­на­рик — не­бра­ко­ван­ный, со­став­ля­ет 1 − 0,02=0,98. Ве­ро­ят­ность того, что мы вы­бе­рем од­но­вре­мен­но два не­бра­ко­ван­ных фо­на­ри­ка равна 0,98 · 0,98 = 0,9604.

Задание№2

Из­вест­но, что в не­ко­то­ром ре­ги­о­не ве­ро­ят­ность того, что ро­див­ший­ся мла­де­нец ока­жет­ся маль­чи­ком, равна 0,512. В 2010 г. в этом ре­ги­о­не на 1000 ро­див­ших­ся мла­ден­цев в сред­нем при­ш­лось 477 де­во­чек. На­сколь­ко ча­сто­та рож­де­ния де­воч­ек в 2010 г. в этом ре­ги­о­не от­ли­ча­ет­ся от ве­ро­ят­но­сти этого со­бы­тия?

Ре­ше­ние. Ча­сто­та cобы­тия «рож­де­ние де­воч­ки» равна 477 : 1000 = 0,477. Ве­ро­ят­ность рож­де­ния де­воч­ки в этом ре­ги­о­не равна 1 − 0,512 = 0,488. По­это­му ча­сто­та дан­но­го со­бы­тия от­ли­ча­ет­ся от его ве­ро­ят­но­сти на 0,488 − 0,477 = 0,011.

Ответ: 0,011.