
Касательная, хорда, секущая, радиус
Подготовка к ОГЭ(модуль геометрия)
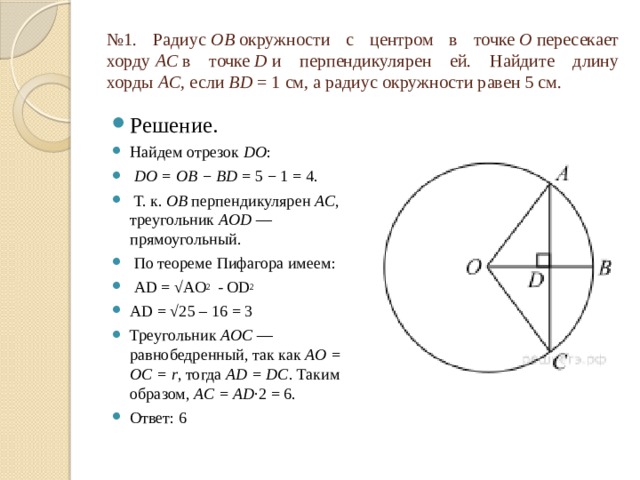
№ 1. Радиус OB окружности с центром в точке O пересекает хорду AC в точке D и перпендикулярен ей. Найдите длину хорды AC , если BD = 1 см, а радиус окружности равен 5 см.
- Решение.
- Найдем отрезок DO :
- DO = OB − BD = 5 − 1 = 4.
- Т. к. OB перпендикулярен AC , треугольник AOD — прямоугольный.
- По теореме Пифагора имеем:
- AD = √AO 2 - OD 2
- AD = √25 – 16 = 3
- Треугольник AOC — равнобедренный, так как AO = OC = r , тогда AD = DC . Таким образом, AC = AD ·2 = 6.
- Ответ: 6
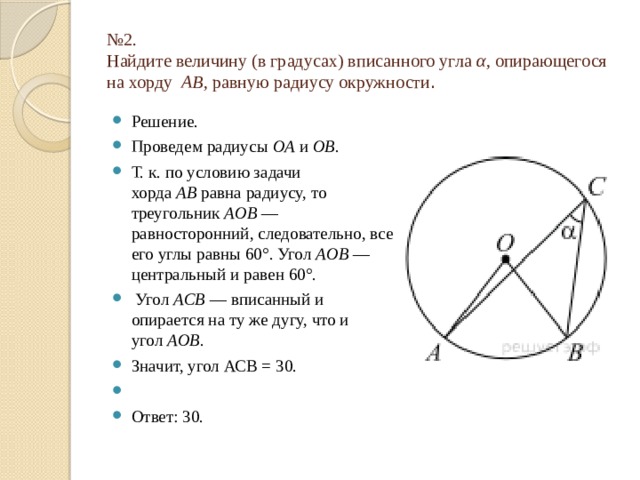
№ 2. Найдите величину (в градусах) вписанного угла α , опирающегося на хорду AB , равную радиусу окружности .
- Решение.
- Проведем радиусы OA и OB .
- Т. к. по условию задачи хорда AB равна радиусу, то треугольник AOB — равносторонний, следовательно, все его углы равны 60°. Угол AOB — центральный и равен 60°.
- Угол ACB — вписанный и опирается на ту же дугу, что и угол AOB .
- Значит, угол АСВ = 30.
-
- Ответ: 30.

№ 3. К окружности с центром в точке О проведены касательная AB и секущая AO . Найдите радиус окружности, если AB = 12 см, AO = 13 см.
- Решение.
- Соединим отрезком точки O и B.
- Полученный отрезок — радиус, проведённый в точку касания, поэтому OB перпендикулярен AB . Рассмотрим прямоугольный треугольник AOB .
- По теореме Пифагора:
- АО 2 = ОВ 2 + АВ 2
- ОВ 2 = АО 2 - АВ 2
- ОВ 2 = 13 2 – 12 2 = 169 – 144 = 25
- ОВ = 5
- Ответ: 5
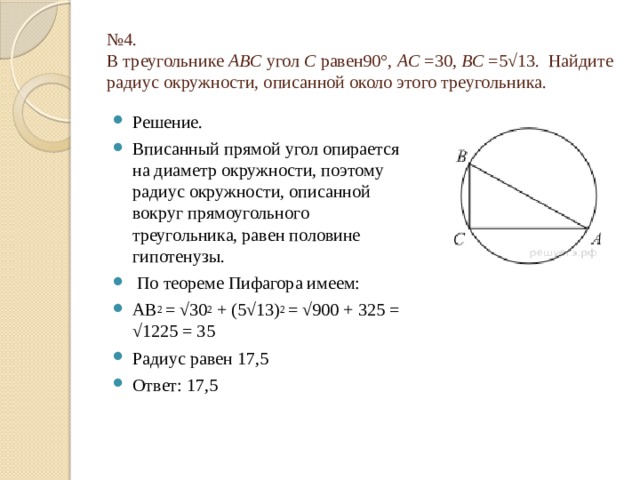
№ 4. В треугольнике ABC угол C равен90°, AC =30, BC =5√13. Найдите радиус окружности, описанной около этого треугольника.
- Решение.
- Вписанный прямой угол опирается на диаметр окружности, поэтому радиус окружности, описанной вокруг прямоугольного треугольника, равен половине гипотенузы.
- По теореме Пифагора имеем:
- АВ 2 = √30 2 + (5√13) 2 = √900 + 325 = √1225 = 35
- Радиус равен 17,5
- Ответ: 17,5

№ 5. Прямая касается окружности в точке K . Точка O — центр окружности. Хорда KM образует с касательной угол, равный 83°. Найдите величину угла OMK . Ответ дайте в градусах.
- Решение.
- Касательная и радиус ОК перпендикулярны.
- Хорда КМ и касательная образуют угол 83 ⁰ .
- Значит, угол ОКМ = 90⁰ – 83⁰ = 7⁰
- В треугольнике OMK :
ОK = OM -радиусы окружности.
- Значит, треугольник OMK — равнобедренный, следовательно, углы при основании равны.
- Угол ОМК = 7 ⁰
- Ответ: 7 ⁰

№ 6. Отрезки AB и CD являются хордами окружности. Найдите длину хорды CD , если AB = 20, а расстояния от центра окружности до хорд AB и CD равны соответственно 24 и 10.
- Решение.
- Рассмотрим треугольники АОН и ВОН – прямоугольные.
- АО = ОВ (радиусы окр), ОН — общая
- Значит, треугольники равны(по гипотенузе и катету).
- АН = ВН = 0,5 АВ.
- Аналогично, СОК = КОD
- СК = КD = 0,5 СD .
- Рассм. треугольник ВОН,
- по теореме Пифагора:
- ОВ = √ОН 2 + ВН 2 = √12 2 + 9 2 = 15
- Рассм. треугольник ОКD ,
- по теореме Пифагора :
- ОK = √OD 2 -KD 2 = √OB 2 - KD 2 = √15 2 -12 2 = 9
- Таким образом, расстояние от центра окружности до хорды СD = 9.
- Ответ: 9

№ 7. Отрезок AB = 40 касается окружности радиуса 75 с центром O в точке B . Окружность пересекает отрезок AO в точке D . Найдите AD .
- Решение.
- Радиус окружности перпендикулярен касательной в точке касания.
- Из прямоугольного треугольника АОВ по теореме Пифагора найдём
- AО = √OB 2 +AB 2 = √40 2 + 75 2 = 85
- АD = AO – OD = 85 – 75 = 15
- Ответ: 15
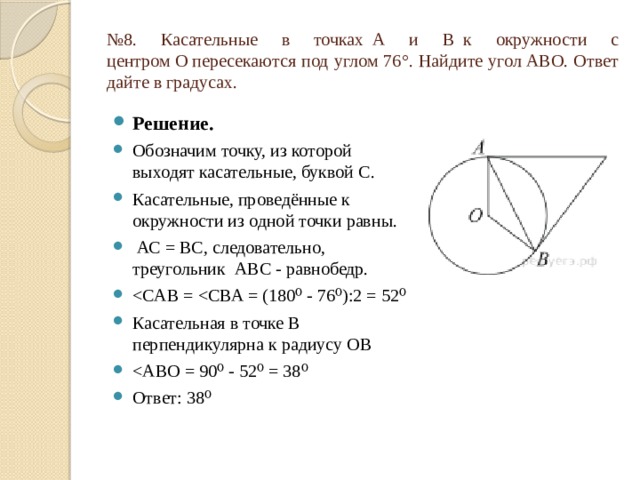
№ 8. Касательные в точках А и В к окружности с центром О пересекаются под углом 76°. Найдите угол АВО. Ответ дайте в градусах.
- Решение.
- Обозначим точку, из которой выходят касательные, буквой С.
- Касательные, проведённые к окружности из одной точки равны.
- АС = ВС, следовательно, треугольник АВС - равнобедр.
- Касательная в точке В перпендикулярна к радиусу ОВ
- Ответ: 38⁰


































