Россия, Хабаровск
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 19.05.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 09.11.2024 12:28
Волкова Инна Борисовна
Преподаватель информатики, Краевое государственное бюджетное профессиональное образовательное учреждение "Хабаровский промышленно-экономический техникум"
48 лет
478
99 095 
Местоположение
Понятие алгоритма. Свойства алгоритмов. Способы описания алгоритмов. Понятие о видах величин.
Категория:
Информатика
03.04.2022 10:28
Просмотр содержимого документа
«Понятие алгоритма. Свойства алгоритмов. Способы описания алгоритмов. Понятие о видах величин.»
Понятие алгоритма. Свойства алгоритмов. Способы описания алгоритмов.
Понятие о видах величин.
Понятие алгоритма в информатике является фундаментальным. Слово это происходит от латинского слова «algorithmi». Так при переводе трактата "Действия с числами (Об индийском счете)" переводчик назвал знаменитого средневекового математика, чье имя –Мухаммед ибн Муса аль-Хорезми, ("Мухаммед сын Мусы из Хорезма"), –жившего в IX веке (783-850гг.) и разработавшего правила арифметических действий над десятичными числами «в столбик»,.
Научное (строгое) определение алгоритма дал А. Черч в 30-х годах. (Тезис Черча: "всякую вычислимую функцию можно представить как рекурсивную"). После Черча и другие математики (А. Тьюринг, Э. Пост, А.Н. Колмогоров, А.А. Марков и др.) давали определение алгоритма. Все эти определения эквивалентны.
АЛГОРИТМ - это конечная последовательность команд (предписаний) исполнителю выполнить эти действия, направленные на достижение поставленной цели или получение решения задачи, однозначно определяемое исходными данными.
АЛГОРИТМ - предписание, однозначно задающее процесс преобразования исходной информации в виде последовательности элементарных дискретных шагов, приводящих за конечное число их применений к результату.
По определению Р. Бауэра алгоритм - это точное, т.е. сформулированное на определенном языке, конечное описание того или иного общего метода, основанного на применении исполнимых элементарных тактов обработки.
Если бы были бы известны алгоритмы решения всех задач, то их исполнение можно было бы поручить машине. Но оказалось, что не все задачи, которые нам хотелось бы решить, имеют алгоритмы решения. Задачи, в принципе не имеющие общего решения, называют алгоритмически неразрешимыми. Например: уравнения выше четвертой степени, задача о трисекции угла, о квадратуре круга (с помощью циркуля и линейки), поиск целочисленных решений произвольного алгебраического уравнения с целыми коэффициентами (10-я проблема Гилберта) и др.
Можно разделить алгоритмы на 3 класса: вычислительные, информационные и управляющие.
Вычислительные алгоритмы имеют дело с простыми типами данных (числами, матрицами), но методы обработки данных могут быть очень сложными и трудоемкими. К ним относятся реализация численных методов на современных ЭВМ, методы оптимизации, теория погрешностей.
В информационных алгоритмах используются сравнительно простые процедуры (например, поиск нужной информации), которые применяют к большим объемам информации. Таковы алгоритмы работы с базами данных. Для эффективной работы информационных алгоритмов необходимо иметь хорошие алгоритмы поиска и сортировки.
В управляющих алгоритмах данные поступают из внешних процессов, которыми алгоритмы управляют. Эти данные во время работы могут меняться очень быстро. Поэтому необходимые управляющие воздействия должны выдаваться в нужный момент, т.е. управляющие алгоритмы должны работать в режиме реального времени.
Не следует считать алгоритм чисто математическим понятием. Каждый из нас ежедневно решает задачи, для описания которых используется тот или иной алгоритм, сформулированный в виде конечной последовательности однозначных предписаний, например, на стене телефона-автомата вы видите инструкцию, цель которой - обеспечить Вам разговор: снять трубку, опустить монету, набрать номер и т.д. Носителями алгоритмов являются разного рода справочники, инструкции и описания гимнастических упражнений. Каждый алгоритм (в быту, в технике и даже в математике) создается в результате обобщения прошлого опыта или технологических разработок и рассчитан на конкретного исполнителя. Многие алгоритмы формулируются неточно, приблизительно, в частности, с учетом уровня исполнителя.
Процесс создания алгоритма–творческий процесс. Он доступен только живым существам. Исполнителем алгоритма является живое существо либо автоматическое устройство, обязанное понимать и исполнять команды алгоритма, но не обязанное вникать в существо дела. Такой субъект или объект называется формальным исполнителем. Примером формального исполнителя является компьютер. Подготовка алгоритмов для компьютера требует их тщательной проработки, т.к. уровень предварительной подготовленности компьютера низок.
Алгоритмы создаются в расчете на конкретного исполнителя с учетом его и только его системы команд.
Процесс подготовки задания для компьютера можно разделить на два общих этапа:
-
создание укрупненного алгоритма (постановка задачи, требования к исходным данным и результатам, описание схемы решения с указанием всех особых ситуаций в виде отдельных блоков);
-
изложение укрупненного алгоритма на языке, понятном машине, - иначе, составление программы решения задачи.
Форма представления укрупненного алгоритма может быть разной: словесное описание, аналитическая (химические, физические, математические формулы), а чаще сочетание и того, и другого. Алгоритм может быть представлен в виде наглядной блок -схемы алгоритма либо в виде некоего псевдокода. Существуют и другие способы представления: операторные схемы алгоритмов (предложены А. А. Ляпуновым), диаграммы смены состояний и т.д.
Свойства алгоритма:
-
- результативность, т.е неизбежность получения конечного результата (решения) после выполнения определенного конечного числа шагов вычислений;
-
- дискретность - алгоритм разбивается на отдельные действия ( дискреты - шаги), каждый из которых четко определен ;
-
- конечность - алгоритм должен приводить к решению за конечное число шагов;
-
- понятность - алгоритм предназначен для конкретного исполнителя и все предписания должны быть ему понятны;
-
- массовость (универсальность)- алгоритм составляется в общем виде для решения некоторого класса однотипных задач.
-
- определенность (детерминированность) - точный и однозначно понимаемый порядок вычислений, что означает, что сколько бы раз не применялся данный алгоритм к одним и тем же исходным данным, каждый раз должен получаться один и тот же результат.
Алгоритм не обязан обладать всеми этими свойствами. Можно выполнять шаги алгоритма не только последовательно, но и параллельно; можно выбирать некий случайный вариант из множества возможных результатов; алгоритм, управляющий работой ядерного реактора, не может быть конечным; существует масса алгоритмов, созданных для уникальных ситуаций (полет к Марсу) .
Объекты, над которыми исполнитель совершает действия, составляют его среду –среду исполнителя. Для математических алгоритмов средой могут быть числа (целые, действительные и т.д., выражения, уравнения и т.п.) –
Способы описания алгоритмов:
- словесный (по шагам);
- графический (в виде блок-схем);
- с использованием псевдокода (псевдоязыка) - в частности, алгоритмического языка КУМИР;
- на языке программирования.
Словесная запись алгоритма обычно используется для алгоритмов, ориентированных на исполнителя -человека. Команды алгоритма могут нумероваться, чтобы иметь возможность на них ссылаться. Форма записи произвольна, в командах помимо слов, могут использоваться символы и формулы. Важно лишь, чтобы каждая команда была понятна исполнителю, точно определяла все его действия и могла быть им выполнена. Она достаточна удобна для записи небольших алгоритмов, для записи алгоритма крупными блоками, для отработки идеи решения.
Примеры: 1.некий человек должен перевезти через реку волка, козу и капусту. Каждый раз он может перевезти только либо волка, либо козу, либо капусту. На одном берегу нельзя оставить вместе козу и волка, козу и капусту (задача встречается в рукописях VIII века).
Возможный алгоритм:
1: перевезти козу.
2: вернуться назад.
3: перевезти волка.
4: вернуться назад с козой.
5: перевезти капусту.
6: вернуться назад.
7: перевезти козу.
2. Алгоритм Евклида для поиска НОД двух чисел, заданный в виде инструкции: «составьте таблицу из двух столбцов Х и У. Первое из данных чисел запишите в столбец Х, а второе – в столбец У. Если данные числа не равны, большее из них замените на результат вычитания от большего числа меньшего. Повторяйте такую операцию до тех пор, пока числа не окажутся равными, после чего число из столбца Х будет искомым результатом».
Блок-схема - представление алгоритмов в виде совокупности геометрических фигур, каждая из которых определяет одно допустимое действие
Графический способ описания алгоритмов нагляден. Блок-схемы алгоритмов состоят из блоков, внутри которых записывают элементы словесной формы записи, например:
- блок начала и блок конца;
- функциональный блок (блок действия)
- информационный блок
- логический блок (блок проверки условия);
- повторение действий, цикл для;
- блок обращения к подпрограмме.
Блоки на схемах соединяются стрелками (либо отрезками, если алгоритм записывается сверху вниз), которые показывают последовательность исполнения команд алгоритма.
Расположение блоков в блок-схеме должно определять порядок действий в алгоритме, и эти действия выполняется сверху - вниз , что указывается с помощью линий, соединяющих блоки. Если необходимо выполнить действия в другом порядке, то соединительные линии должны иметь стрелку для указания направления действия. Внутри блока может быть краткая характеристика выполняемого действия (на естественном языке с элементами математической символики). Каждый блок имеет один вход и один выход..
Пример: алгоритм поиска НОД двух чисел:
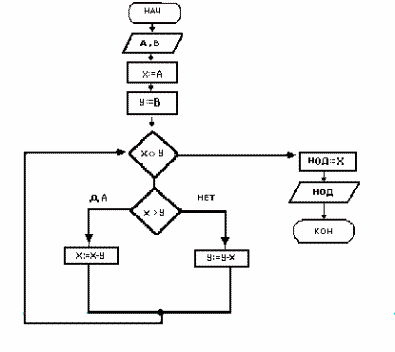
Псевдокод представляет собой систему обозначений и правил, предназначенных для единообразной записи алгоритмов. С одной стороны, он близок к обычному естественному языку, поэтому алгоритмы могут на нем записываться и читаться как обычный текст. С другой стороны, в нем используются некоторые формальные конструкции и математическая символика, что приближает запись алгоритма к общепринятой математической записи.
В нем, так же как и в формальных языках, есть служебные слова, смысл которых определен раз и навсегда . Они выделяются в печатном тексте жирным шрифтом, а в рукописном тексте подчеркиваются. В псевдокоде не приняты строгие синтаксические правила для записи команд. Он, т.е. псевдокод, ориентирован на человека. Пример псевдокода см. далее в виде краткого описания языка Кумир.
Пример Алгоритм Евклида для поиска НОД двух чисел, записанный на языке Кумир:
алг НОД (арг цел а,b, рез цел нод )
арг! a,b
рез! нод
нач цел x,y
x:=a
y:=b
нц пока xy
если xy
то x:=x-y
иначе y:=y-x
все
кц
нод:=х
кон
Язык для записи алгоритма должен быть формализован. Такой язык принято называть языком программирования, а запись алгоритма на этом языке - программой для ЭВМ. Под программированием понимают составление программы (т.е. последовательности инструкций) для компьютера, описывающей процесс решения задачи.
Языки классифицируют по разным уровням, учитывая степень зависимости языка от конкретной ЭВМ.
На самом нижнем уровне классификации находится машинный язык, т.е. внутренний язык ЭВМ, на которым в конечном итоге представляется и исполняется программа.
Разработчики алгоритмов используют, как правило, языки программирования более высокого уровня, в которых принята символическая форма записи, близкая к общепринятой математической.
При исполнении алгоритма на ЭВМ программа транслируется с языка высокого уровня на машинный язык, а затем уже исполняется.
Пример Алгоритм Евклида для поиска НОД двух чисел, записанный на языке turbo Pascal:
var a,b,x,y,nod: integer;
begin
read (a,b); x:=a; y:=b;
while xy do
if xy then x:=x-y else y:=y-x;
nod:= x;
end.
Величины
Алгоритмы, предназначенные для решения широкого круга практических задач, связаны с преобразованием информации. При этом под информацией понимают вполне конкретные величины - числовые, текстовые, графические и т.п. Для описания величины необходимо указать ее имя, вид, тип, значение.
Все величины при описании алгоритма обозначаются именами (идентификаторами). Принято считать, что именем может быть любая последовательность букв, цифр и знака подчеркивания, начинающаяся с буквы, например x, xl, alfa, B12C и т.п..
Величины делятся на постоянные (те, что не меняются в процессе исполнения алгоритма) и переменные (меняющиеся в процессе исполнения). Можно величины разделить и как величины-аргументы и как величины-результаты, и как промежуточные величины. Т.о. вид величины характеризует ее использование в алгоритме, роль содержащейся в величине информации.
Величины делятся на числовые и нечисловые. Примерами нечисловых величин могут быть литерные ( значениями их являются слова или текст), логические («да» или «нет», (другими словами «истина» либо «ложь»)), символьные (ее значением может быть только один символ). Числовые величины могут быть целыми и вещественными. Необходимость различать их связана с особенностями ЭВМ: целые числа представляются в памяти машин точно ( из некоторого диапазона), а вещественные – приближенно. Т.е. тип величины задает множество допустимых значений величины и множество разрешенных операций с нею.
Имя, тип, вид величины не могут меняться, а значение величины может многократно меняться в процессе работы алгоритма.
Структуры алгоритмов.
Алгоритмы можно представлять как некоторые жесткие структуры, состоящие из отдельных базовых элементов.
Простые команды. Элементарной структурной единицей любого алгоритма является простая команда, обозначающая один элементарный шаг переработки или отображения информации .
При исполнении алгоритма переработка информации состоит в изменении значения некоторых величин, с которыми работает алгоритм.
Значение переменной величины может быть изменено с помощью команды присваивания, имеющей вид
идентификатор:=выражение
В реальных командах «идентификатор» и «выражение» заменяются на конкретные имена и конкретные выражения. Знак присваивания (:=) обозначают указание исполнителю выполнить действие, состоящие в том, чтобы, во-первых, вычислить значение выражения , стоящего в правой части команды присваивания, и, во-вторых, присвоить это значение переменной, имя которой стоит в левой части команды.
Переменной величине может быть присвоено значение и с помощью команды ввода, которая передает исполнителю значение переменной из некоторого внешнего источника.
Например, команда ввод (x , y) означает, что исполнитель получает из внешнего источника два значения, которые должны быть присвоены переменным x и y.
Последовательность из нескольких команд алгоритма, выполняющихся одна за другой, называется серией.
Составные команды .Из простых команд и проверки условий образуются составные команды , имеющие более сложную структуру.
1. СЛЕДОВАНИЕ - команды выполняются одна за другой в том порядке, в котором записаны в программе;
В виде б
лок-схемы на КУМИРЕ:
. . .
серия 1 Действие 1
серия 2 Действие 2 
. . .
2. ВЕТВЛЕНИЕ (выбор) - данные влияют на ход выполнения программы. В программе заложены разные пути следования и по ходу действия выбирается один из возможных вариантов в зависимости от условия. Условие есть некоторое логическое выражение (некий вопрос), его значением могут быть логические константы «да» или «нет».
Полная форма команды ветвления:
В виде
б лок-схемы: на КУМИРЕ:
если условие
да нет то действие 1
условие иначе действие 2
Действие 2
все
Действие 1
Сокращенная форма команды ветвления:
В виде
блок-схемы: на КУМИРЕ:
да нет если условие
усл. то действие 1
все
действие 1
-
ЦИКЛ (повторение) - Иногда в процессе работы алгоритма определенный набор команд выполняется многократно. Многократно выполняемую часть вычислительного процесса называют циклом. Условие, содержащееся в цикле, используется для определения количества повторений. Различают циклы со счетчиком и итерационные циклы. В случае, когда известно число повторений цикла, получаем циклы со счетчиком. В случае же, когда нужно произвести вычисления с заданной точностью и условием выхода из цикла является достижение этой точности, имеем итерационный цикл. В данном цикле количество повторений цикла - число итераций неизвестно.
Цикл может записываться тремя формами: цикл ПОКА, цикл ДЛЯ, цикл ДО.
Команда ПОКА (команда повторения с предусловием) универсальна, используется, когда неизвестно число повторений в цикле: ( пока условие истинно, выполнять действия тела цикла).
В виде блок-схемы на КУМИРЕ
нц пока условие
провер- нет действие
ка усл.повто-
рения . . .
Тело цикла
да кц
(нц - начало цикла , кц -конец цикла)
Команда ДЛЯ используется, когда известно число повторений в цикле
В виде блок-схем: на КУМИРЕ
нет нц для параметр от нз до кз
параметр от нз до кз
. . .
да Тело цикла
Тело цикла кц
где : нз - начальное значение, кз - конечное значение параметра цикла.
Цикл ДО (команда повторения с постусловием) выполняется аналогично, только условие проверяется после выполнения команды, а повторение выполнения команды (тела цикла) происходит в том случае, когда условие не соблюдено, т.е. выполнение команды производится до проверки условия (хотя бы один раз).
В виде блок-схемы:
повторять
Действие
условие да до
нет
В теории алгоритмов доказано (Дейкстра Э.), что алгоритм любой задачи можно описать, используя комбинацию 3-х типов управляющих структур: следования, развилки и цикла. Это превращает построение алгоритма в ‘сборку’ его конструкции из имеющегося набора базовых конструкций. ‘Сборка’ алгоритмов может происходить двумя путями:
во-первых, базовые элементы могут соединяться в последовательность, образуя конструкцию следования;
во-вторых, одна базовая конструкция может вкладываться в другую конструкцию, образуя ‘вложенные’ конструкции.
4. Вспомогательные (подчиненные) алгоритмы (ВА). Иногда при составлении некоторого алгоритма возникает необходимость использования в разных его местах одного и того же набора действий. Бывает так, что при построении алгоритма становится возможным использование уже разработанных ранее алгоритмов. Чтобы не записывать этот повторяющийся набор несколько раз, его выносят из основного алгоритма и оформляют в виде отдельного (вспомогательного) алгоритма, которому дают имя. После этого в основном алгоритме в соответствующем месте достаточно записать имя вспомогательного алгоритма, чтобы выполнился набор действий, входящих в него. Готовые алгоритмы, целиком включаемые в состав разрабатываемого алгоритма называются вспомогательными или подчиненными алгоритмами в отличие от главного или основного алгоритма, в состав которого они включаются. Вспомогательные алгоритмы, записанные на языках программирования, называются подпрограммами или процедурами. Использование вспомогательного алгоритма позволяет сделать запись основного алгоритма меньшей по объему и более понятной.
В заголовке ВА следом за именем может указываться в круглых скобках список формальных параметров. Такой подчиненный алгоритм называют алгоритмом с параметрами. В списке формальных параметров указываются имена входных и выходных величин (аргументов и результатов) алгоритма.
Ссылка на ВА в основном алгоритме осуществляется с помощью специальной команды вызова ВА, в которой указываются имя подчиненного алгоритма и список фактических параметров, которые должны быть подставлены вместо формальных параметров при исполнении ВА. Таким образом, команда вызова ВА имеет вид
().
Исполнение такой команды эквивалентно исполнению команд вспомогательного алгоритма
Команда вызова ВА записывается внутри следующей фигуры в случае записи алгоритма в виде блок-схемы:
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
Полезное для учителя
Реализация образовательных программ осуществляется с применением исключительно электронного обучения и ДОТ
