Популяционная генетика. Закон Харди-Вайнберга

ПОПУЛЯЦИОННАЯ ГЕНЕТИКА.

ЗАКОН ХАРДИ-ВАЙНБЕРГА

Популяция – это совокупность особей одного вида, длительно занимающих определенный ареал, свободно скрещивающихся между собой и относительно изолированных от других особей вида.

Основная закономерность, позволяющая исследовать генетическую структуру больших популяций, была установлена в 1908 году независимо друг от друга английским математиком Г. Харди и немецким врачом В. Вайнбергом.

Закон Харди-Вайнберга: в идеальной популяции соотношение частот генов и генотипов – величина постоянная из поколения в поколение.

Признаки идеальной популяции: численность популяции велика, существует панмиксия (нет ограничений к свободному выбору партнера), отсутствуют мутации по данному признаку, не действует естественный отбор, отсутствуют приток и отток генов.

Первое положение закона Харди-Вайнберга гласит: сумма частот аллелей одного гена в данной популяции равна единице. Это записывается следующим образом:

p + q = 1,

где p – частота доминантного аллеля А, q - частота рецессивного аллеля а. Обе величины обычно принято выражать в долях единицы, реже – в процентах (тогда p + q = 100 %).

Второе положение закона Харди-Вайнберга: сумма частот генотипов по одному гену в данной популяции равна единице. Формула для вычисления частот генотипов имеет следующий вид:

p² + 2pq +q² = 1,

где p² – частота гомозиготных особей по доминантному аллелю (генотип АА), 2pq – частота гетерозигот (генотип Аa), q² – частота гомозиготных особей по рецессивному аллелю (генотип аа).

Вывод этой формулы: в равновесной популяции женские и мужские особи имеют одинаковые частоты как аллеля А (p), так и аллеля а (q). В результате скрещивания женских гамет ♀(p + q) с мужскими ♂(p + q) и определяются частоты генотипов: (p + q) (p + q) = p² + 2pq +q² .

Третье положение закона: в равновесной популяции частоты аллелей и частоты генотипов сохраняются в ряде поколений.

1. В популяции, подчиняющейся закону Харди-Вайнберга, частоты аллелей А и а соответственно равны 0,8 и 0,2. Определите частоты гомозигот и гетерозигот по этим генам в первой генерации.

Решение. Частоты генотипов вычисляются по уравнению Харди-Вайнберга:

p² + 2pq + q² = 1,

где p – частота доминантного гена, и q – частота рецессивного гена.

В данной задаче частота аллеля А равна 0,8, а частота аллеля а равна 0,2. Подставив эти числовые значения в уравнение Харди-Вайнберга, получим следующее выражение:

0,8² + 2  0,8  0,2 + 0,2² = 1 или 0,64 + 0,32 + 0,04 = 1

Из уравнения следует, что 0,64 – частота доминантного гомозиготного генотипа (АА), а 0,04 – частота рецессивного гомозиготного генотипа (аа). 0,32 – частота гетерозиготного генотипа (Аа).

2. В популяции лисиц на 1000 рыжих встречаются 10 белых особей. Определите процентное соотношение рыжих гомозиготных, рыжих гетерозиготных и белых лисиц в данной популяции.

Решение.

По уравнению:

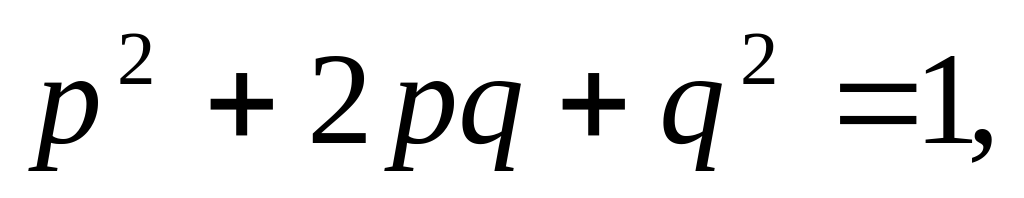
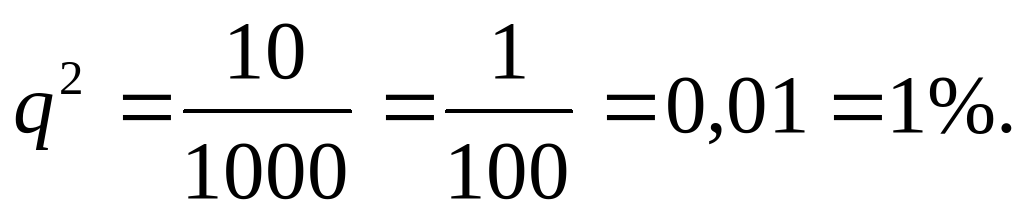
Таким образом, рыжих гомозиготных лисиц в популяции 81%, рыжих гетерозиготных – 18%, белых лисиц – 1%.

3. Аллель кареглазости доминирует над голубоглазостью. В популяции оба аллеля встречаются с равной вероятностью.

Отец и мать кареглазые. С какой вероятностью следует ожидать, что родившийся у них ребенок будет голубоглазым?

Решение. Если в популяции оба аллеля встречаются одинаково часто, то в ней 1/4 доминантных гомозигот, 1/2 гетерозигот (и те и другие кареглазые) и 1/4 рецессивных гомозигот (голубоглазые). Таким образом, если человек кареглазый, то два против одного, что это гетерозигота. Итак, вероятность оказаться гетерозиготой 2/3. Вероятность передать потомству аллель голубоглазости равна 0, если организм гомозиготен, и 1/2, если он гетерозиготен. Полная вероятность того, что данный кареглазый родитель передаст потомству аллель голубых глаз, равна 2/3×1/2, т.е. 1/3. Чтобы ребенок был голубоглазым, он должен получить от каждого из родителей по аллелю голубых глаз. Это произойдет с вероятностью 1/3×1/3=1/9.

4. Кистозный фиброз поджелудочной железы поражает индивидуумов с рецессивным гомозиготным фенотипом и встречается среди населения с частотой 1 на 2000. Вычислите частоту носителей.

Решение. Носители являются гетерозиготами. Частоты генотипов вычисляются по уравнению Харди-Вайнберга:

p² + 2pq + q² = 1,

где p² – частота доминантного гомозиготного генотипа, 2pq – частота гетерозиготного генотипа и q² – частота рецессивного гомозиготного генотипа.

Кистозный фиброз поджелудочной железы поражает индивидуумов с рецессивным гомозиготным фенотипом; следовательно, q² = 1 на 2000, или 1/2000 = 0,0005. Отсюда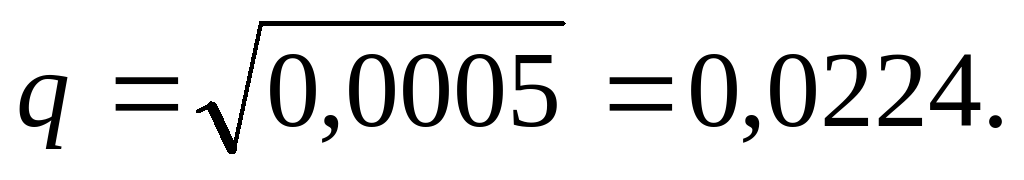

Поскольку, p + q = 1, p = 1 – q = 1 – 0,0224 = 0,9776.

Таким образом, частота гетерозиготного фенотипа (2pq) = 2  (0,9776)  (0,0224) = 0,044 = 1 на 23  5%, т.е. носители рецессивного гена кистозного фиброза поджелудочной железы составляют около 5% от популяции.

5. При обследовании населения города N (100000 человек) обнаружено 5 альбиносов. Установить частоту встречаемости гетерозиготных носителей гена альбинизма.

Решение. Так как альбиносы являются рецессивными гомозиготами (аа), то, согласно закону Харди-Вайнберга: 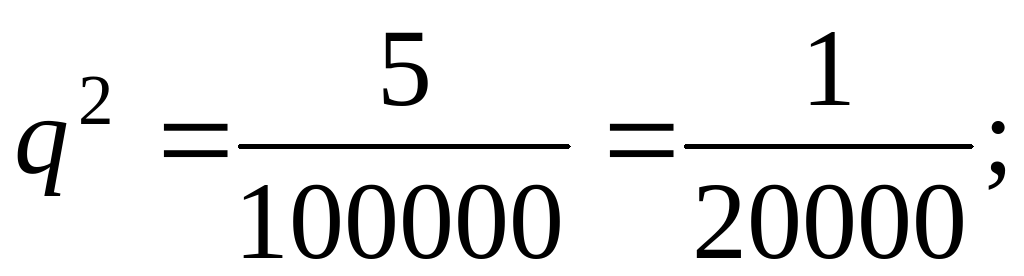частота рецессивного гена 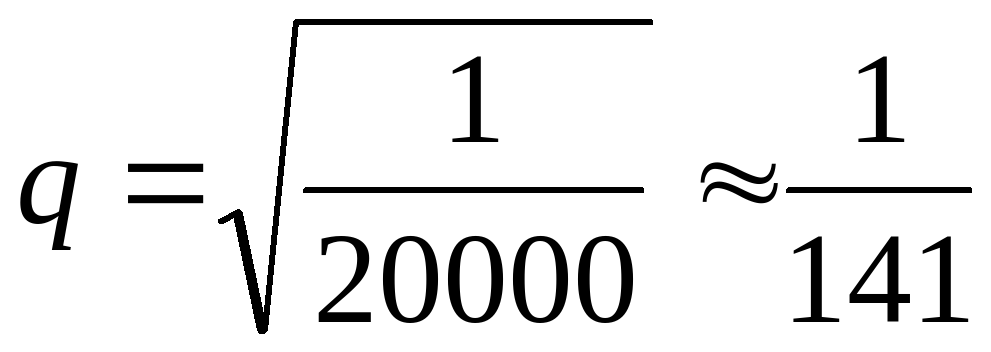, p + q = 1, отсюда, p = 1 – q; 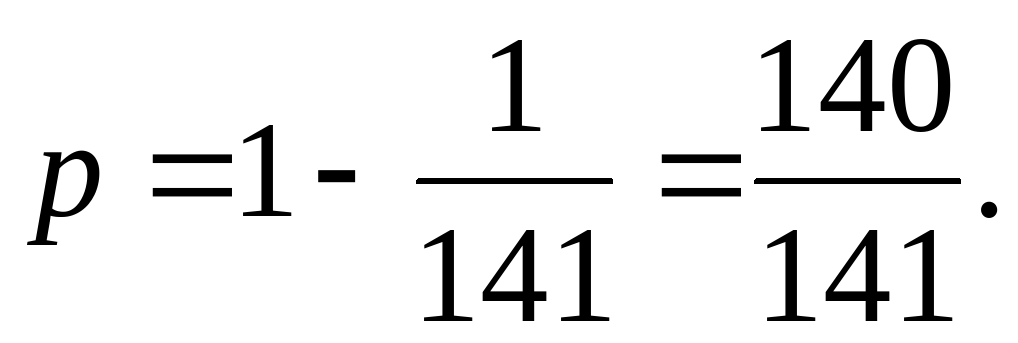Частота гетерозигот составляет 2pq.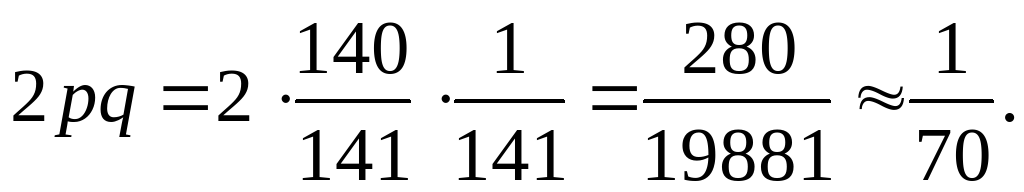

Следовательно, каждый 70-й житель города N является гетерозиготным носителем гена альбинизма.

6. В популяции из 5000 человек 64% способны свертывать язык трубочкой (доминантный ген R), а 36% такой способностью не обладают (рецессивный ген r). Вычислите частоты встречаемости генов R и r и генотипов RR, Rr и rr в популяции.

Решение. Частота встречаемости лиц с генотипами RR и Rr равна 0,64, а гомозигот rr (q²) = 0,36. Исходя из этого, частота гена r равна 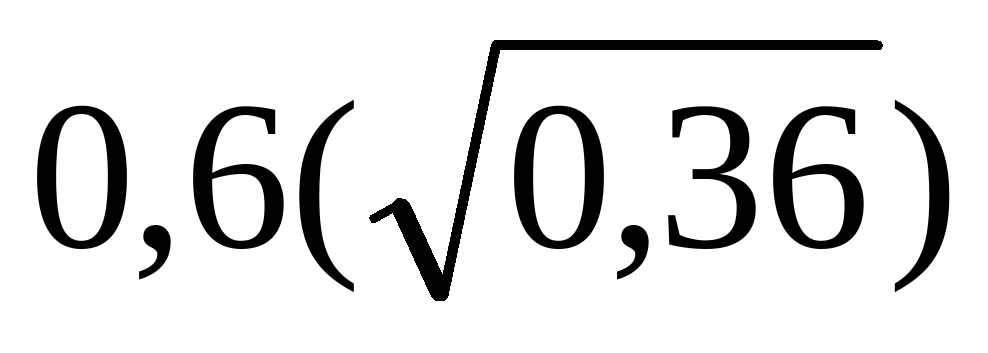. А поскольку p + q = 1, то p = 1 – q = 0,4, т.е. частота аллеля R(p) составляет 0,4. Если p = 0,4, то p² = 0,16. Значит, частота встречаемости лиц с генотипом RR составляет 16%.

Итак, частоты встречаемости генов R и r 0,4 и 0,6. Частоты генотипов RR, Rr и rr составляют, соответственно, 0,16, 0,48 и 0,36.

7. В популяции встречаются три генотипа по гену альбинизма а в соотношении: 9/16 АА, 6/16 Аа и 1/16 аа. Находится ли данная популяция в состоянии генетического равновесия?

Решение. Известно, что популяция состоит из 9/16 АА, 6/16 Аа и 1/16 аа генотипов. Соответствует ли такое соотношение равновесию в популяции, выражаемому формулой Харди-Вайнберга?

После преобразования чисел становится ясным, что популяция по заданному признаку находится в состоянии равновесия: (3/4)² АА : 2  3/4  1/4 Аа : (1/4)² аа. Отсюда