«Построение объемных фигур и сечений в GeoGebra 3D»

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«МОРДОВСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ ИНСТИТУТ

ИМЕНИ М. Е. ЕВСЕВЬЕВА»

Физико-математический факультет

Кафедра информатики и вычислительной техники

РЕФЕРАТ

на тему:

«Построение объемных фигур и сечений в GeoGebra 3D»

Выполнила:

студентка 5 курса группы МДМ-213

Сурдина А. А.

Проверила:

кандидат физико-математических наук, доцент

Кормилицына Т. В.

Саранск 2018

Введение

GeoGebra – это бесплатная, кроссплатформенная динамическая математическая программа для всех уровней образования, включающая в себя геометрию, алгебру, таблицы, графы, статистику и арифметику, в одном удобном для использования пакете.

Кроме того, у программы богатые возможности работы с функциями (построение графиков, вычисление корней, экстремумов, интегралов и т.д.) за счёт команд встроенного языка (который, кстати, позволяет управлять и геометрическими построениями).

В отличии от других программ для динамического манипулирования геометрическими обьектами, идея GeoGebra заключается в интерактивном сочетании геометрического, алгебраического и числового представления. Вы можете создавать конструкции с точками, векторами, линиями, коническими сечениями, а также математическими функциями, а затем динамически изменять их.

Кроме того, GeoGebra позволяет напрямую вводить уравнения и манипулировать координатами. Таким образом, можно легко составлять графики функций, работать со слайдерами для подбора необходимых параметров, искать символические производные, и использовать мощные команды вроде корня и последовательности.

Интерфейс программы GeoGebra (ГеоГебра) напоминает классную доску, на которой можно рисовать графики, создавать геометрические фигуры и т.п. В окне программы будет наглядно отображены производимые изменения: если вы измените уравнение, кривая перестроится, изменится масштаб или ее положение в пространстве, уравнение, написанное рядом с кривой, автоматически будет скорректировано, согласно новым значениям.

Программу GeoGebra широко используют в мире миллионы пользователей для обучения алгебре и геометрии. Процесс обучения нагляден благодаря визуальной форме использования приложения.

Возможности программы по математике не ограничиваются только построением графиков, программу GeoGebra можно будет использовать для интерактивных чертежей при решении геометрических задач. Программа ГеоГебра обладает мощными и функциональными возможностями, которые позволяет наглядно и просто обучаться математике.

Приложение включает в себя геометрию, алгебру, есть возможность совершать арифметические операции, создавать таблицы, графики, возможна работа со статистикой, работа с функциями, поддерживается создание анимации и т.д. В программе GeoGebra можно будет создавать различные 2D и 3D фигуры, интерактивные ролики, которые затем можно будет размещать в интернете.

Все приложения, входящие в состав программы GeoGebra, доступны и синхронизируются между собой для работы в составе одного пакета.

GeoGebra была создана Маркусом Хохенвартером. Программа написана на языке Java, приложение поддерживает работу в различных операционных системах: Windows, Mac OS X, Linux, Android.

С сайта производителя можно будет скачать обычную версию программы GeoGebra для установки на компьютер. Также можно будет скачать переносную версию программы (GeoGebra Portable) для соответствующей операционной системы.

После запуска GeoGebra на компьютере, ознакомимся с интерфейсом программы.

1. Интерфейс GeoGebra

При запуске окно программы имеет вид, приведенный на рисунке 1.

Интерфейс программы GeoGebra напоминает графический редактор. Программу можно использовать для черчения, но это не основное предназначение приложения.
Основные элементы интерфейса программы GeoGebra:

1. Полоса меню. Из меню можно изменить настройки программы.

2. Панель инструментов. Здесь находятся инструменты для создания объектов. После щелчка по треугольнику в правом нижнем углу кнопки, будут открыты дополнительные инструменты. Операции, доступные в панели инструментов, можно производить с помощью строки ввода.

3. Панель объектов. В Панели объектов отображаются введенные переменные и функции. Вместо имен переменных здесь отображаются их значения. Для того, чтобы увидеть формулу в символьном виде, нужно будет кликнуть по ней правой кнопкой мыши.

4. Кнопки «Отменить» и «Повторить».

5. Строка ввода. Это основной инструмент при работе в программе GeoGebra. Здесь вводятся команды и формулы, задаются значения переменных. Справа от строки ввода расположена кнопка «Список команд». С помощью дополнительных команд можно будет вводить команды и отсутствующие на клавиатуре символы.

6. Рабочая область. Все построения в программе производятся в рабочей области. Вы можете изменить масштаб с помощью колесика мыши, перемещать по рабочей области ось координат.

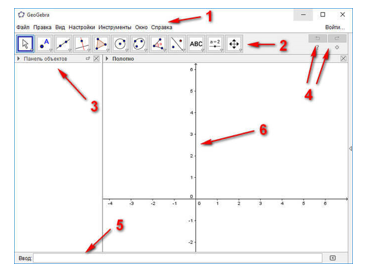
Рис 1 – Интерфейс программы GeoGebra

2. Использование инструментов для построений в Geogebra 3D

Для открытия полотна 3D нужно перейти в строке меню вкладку вид (Рисунок 2)

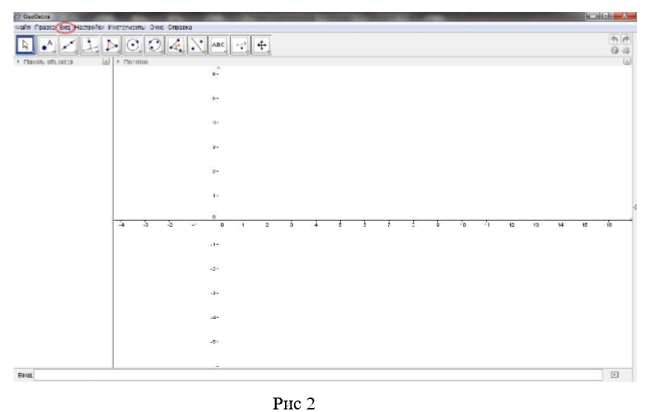
Легким нажатием мыши на вкладку Полотно 3D GeoGebra превращается в 3D конструктор (Рисунок 3а и 3б)

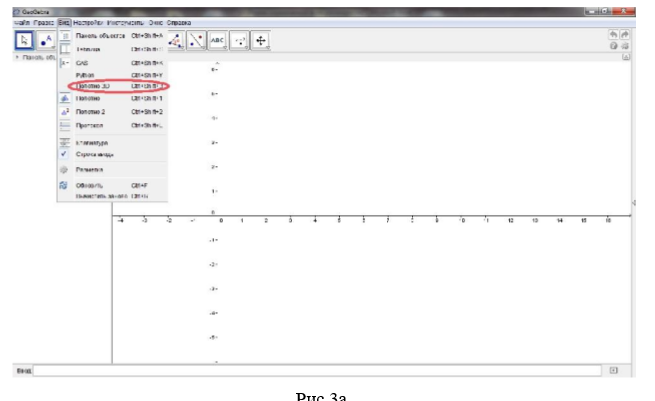
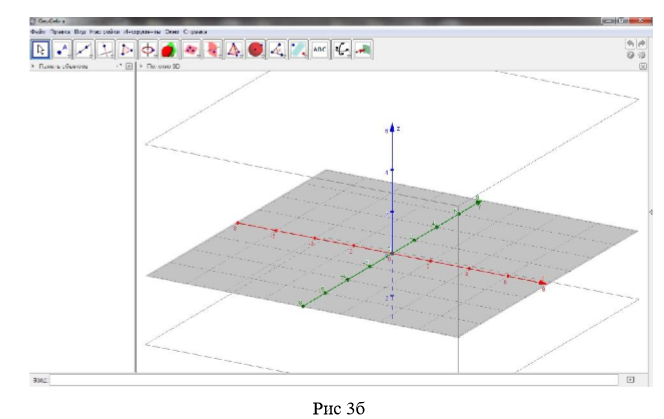
Самыми важными фигурами в геометрии являются пирамида и призма, поэтому данная подгруппа функций именно для этих фигур. Функции Пирамида и Призма позволяют строить данные фигуры через любые точки и в любой плоскости оси координат ( Рисунок 4).

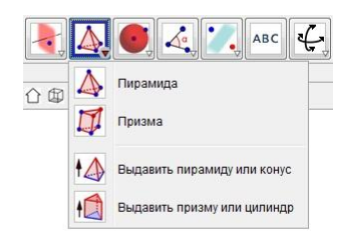
Рис 4 – Функции Пирамиды и Призмы

С помощью функций Выдавить пирамиду или конус и Выдавить призму или цилиндр возможности построения увеличиваются в двойне. Последняя подгруппа функций которую хочу представить это функции Сфера по точке и центру, Сфера по центру и радиусу, Cone и Cylinder (Рисунок 5 ). Как видно по названиям эта подгруппа специализируется по строению сферических фигур.

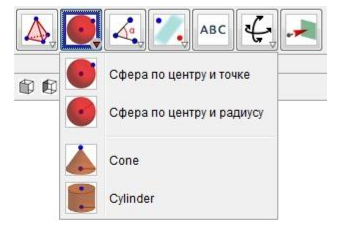
Рис 5 – Функции Сферы

3. Построение объемных фигур

1. Построение призмы.

Задача. Построить призму ABCD..G.

Решение: 1) Нужно выбирать функцию Призма и отметить 4 точки на координатной оси как показано на рисунке.

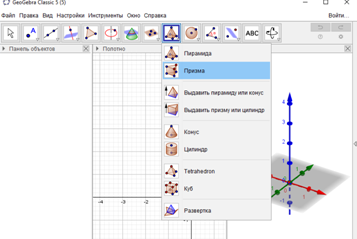
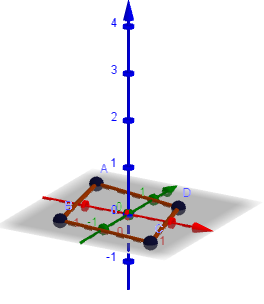
2) Нажимая по оси z на нужную высоту получится призма ABCD..G.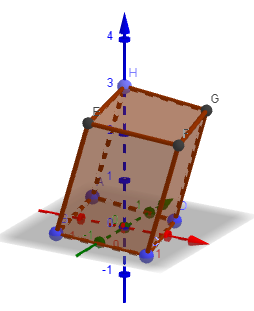

2. Построение пирамиды

Задача. Построить пирамиду SABCDE.

Решение: 1) Нужно выбрать функцию Пирамида и отметить 4 точки на координатной оси как показано на рисунке.

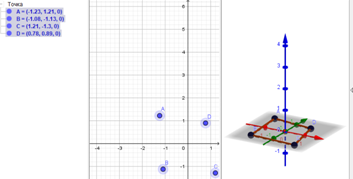
2) Нажать по оси z на нужную высоту и после переименования точки на осиz получим пирамиду SABCDE

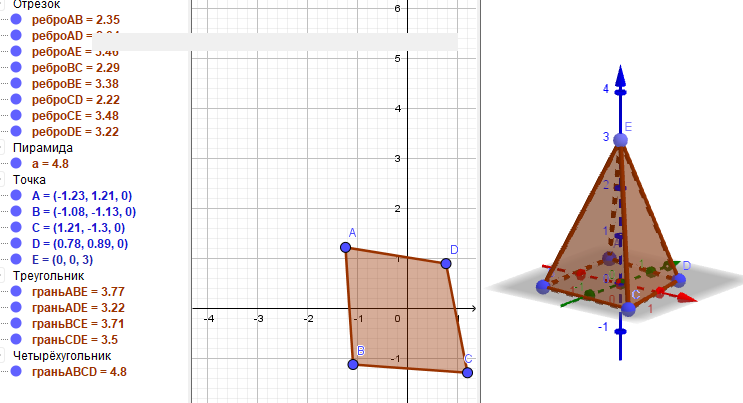
3. Построение прямоугольного параллелепипеда

Задача. Построить прямоугольный параллелепипед ABCD..G.

Решение: При помощи строки ввода ставим 4 точки на плоскость XOYи одну точку на плоскость XYZ как показано на рисунке.

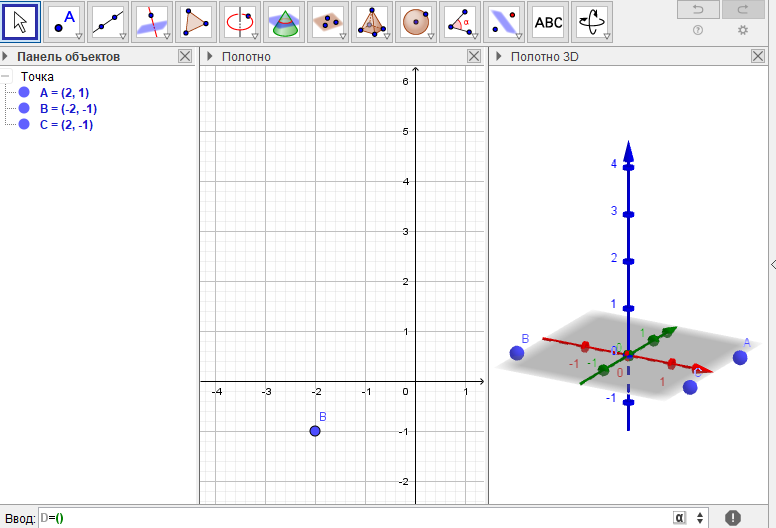
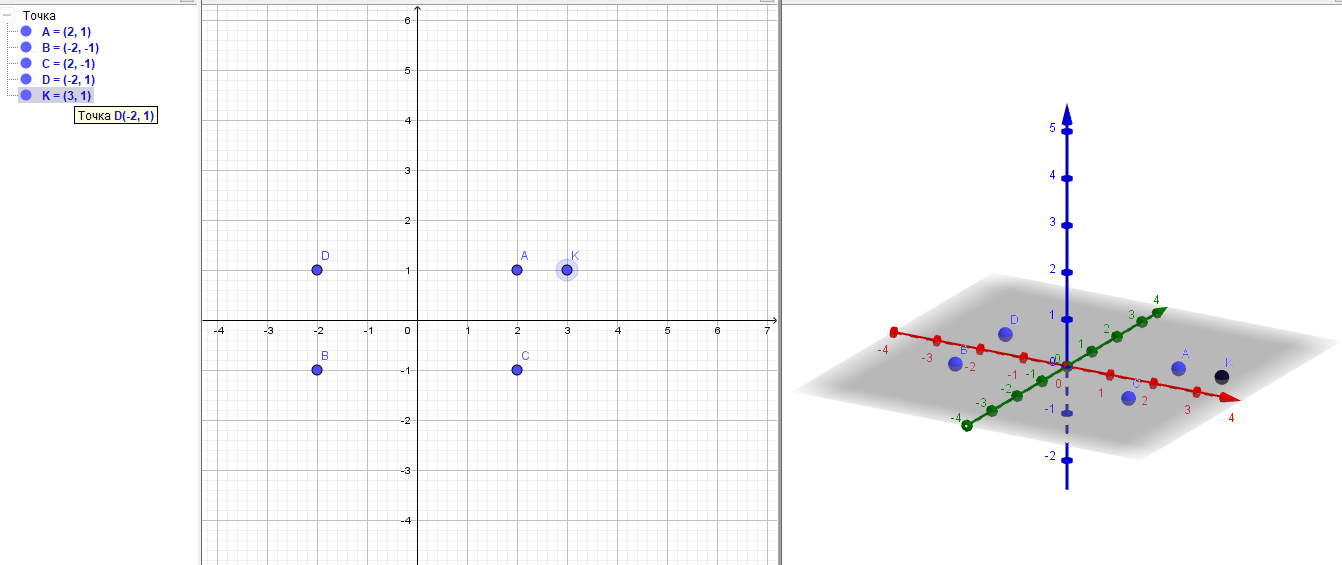
2) После выполнения вышеуказанных действий выбираем опцию Призма соединяем точки A,B,C,D потом нажимаем на точку и получаем прямоугольный параллелепипед ABCD..F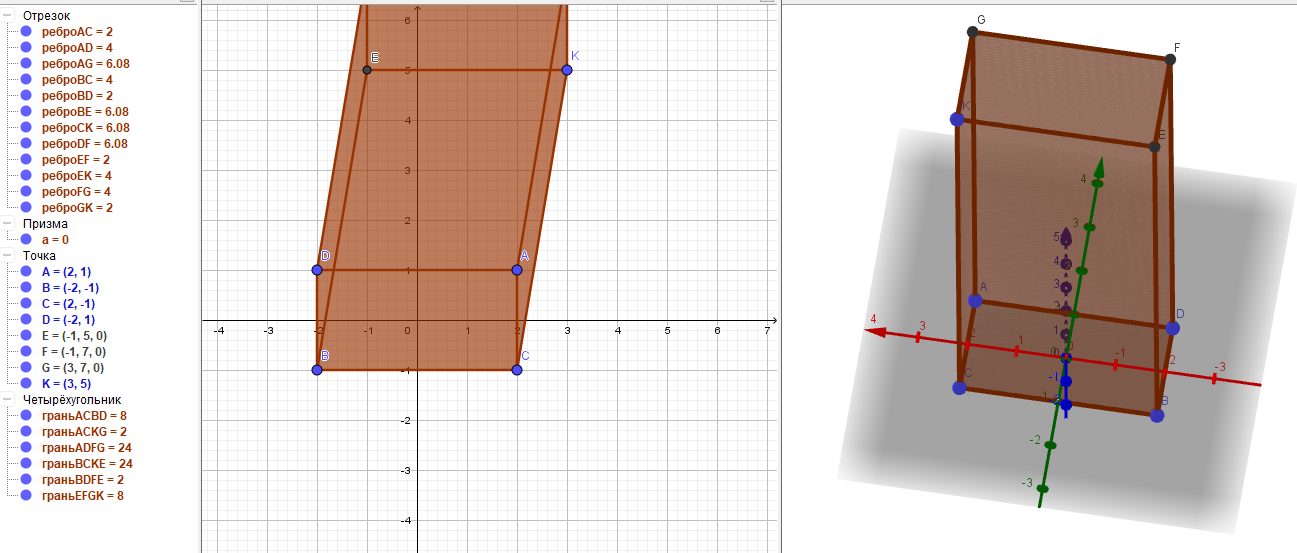

4. Построение цилиндра

Задача. Построить цилиндр с радиусом 3.

Решение: Для построения цилиндра есть опция Цилиндр. Выбираем эту опцию и на оси z выбираем две точки после чего выйдет окно с запросом на радиус как на рисунке 14.

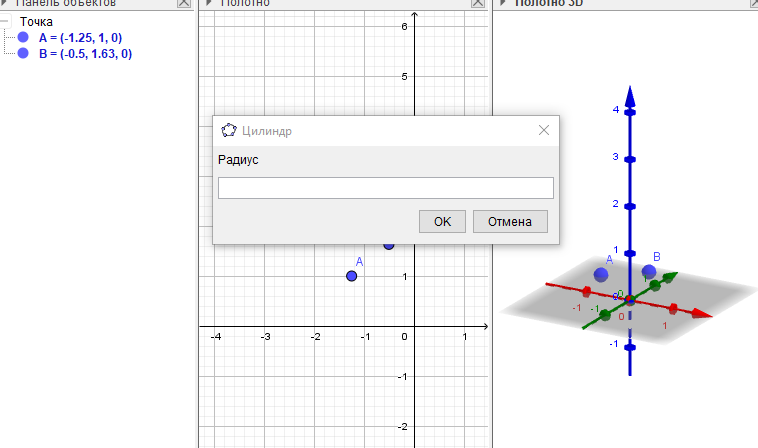
Рис 14 – Окно с запросом на радиус

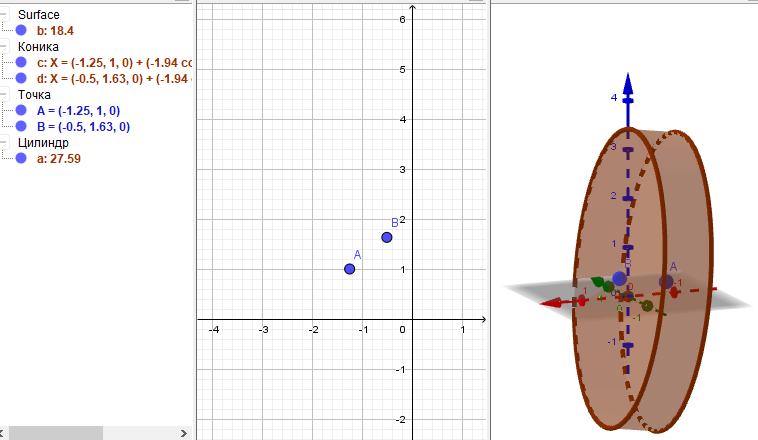
Вводим значение радиуса и имеем цилиндр с данным радиусом

5. Построение конуса

Задача. Построить конус с радиусом 3.

Решение: Для построения конуса есть опция Cone. Выбираем эту опцию и на оси z выбираем две точки после чего выйдет окно с запросом на радиус как на рисунке 16.

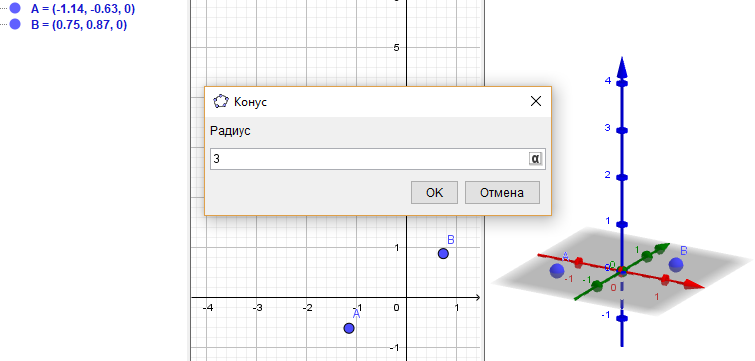
Рис 16 – Окно с запросом на радиус

Вводим значение радиуса и имеем конус с данным радиусом.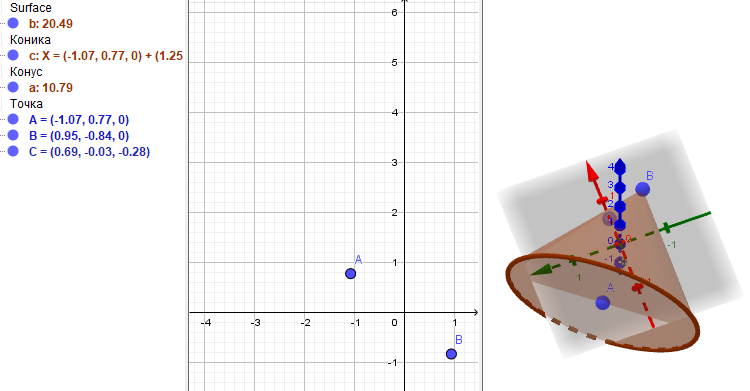

4. Построение плоских сечений

1. Построение сечения пирамиды

Задача 1. На ребрах AB, BC и CD тетраэдра ABCD отмечены точки M, N и P. Построить сечение тетраэдра плоскостью MNP.

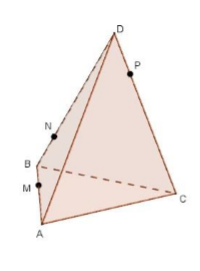
Решение: Построим сначала прямую, по которой плоскость MNP пересекается с плоскостью грани ABC. Точка M является общей точкой этих плоскостей. Для построения еще одной общей точки продолжим отрезки NP и BC до их пересечения в точке E, которая и будет второй общей точкой плоскостей MNP и ABC. Следовательно, эти плоскости пересекаются по прямой ME.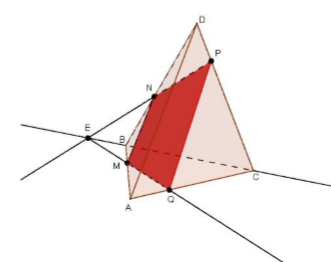

Прямая ME пересекает ребро AC в некоторой точке Q. Четырехугольник MNPQ – искомое сечение.

Задача 2. Точка M лежит на боковой грани ADB тетраэдра DABC (рис.3). Построить сечение тетраэдра плоскостью, проходящей через точку M параллельно основанию ABC.

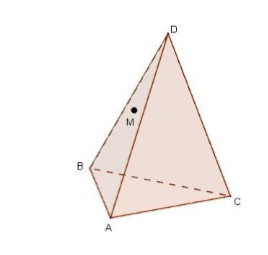
Решение: Так как секущая плоскость параллельна плоскости ABC, то она параллельна прямым AB, BC и CA. Следовательно, секущая плоскость пересекает боковые грани тетраэдра по прямым, параллельным сторонам треугольника ABC. Отсюда вытекает следующий способ построения искомого сечения. Проведём через точку M прямую, параллельную отрезку AB, и обозначим буквами P и Q точки пересечения этой прямой с боковыми ребрами DA и DB. Затем через точку P проведем прямую, параллельную отрезку AC, и обозначим буквой R точку пересечения этой прямой с ребром DC. Треугольник PQR–искомое сечение.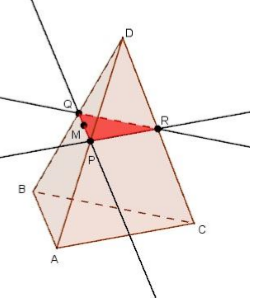

1. Построение сечения прямоугольного параллелепипеда

Задача 1. На ребрах параллелепипеда даны три точки A, B и C. Построить сечение параллелепипеда плоскостью ABC.

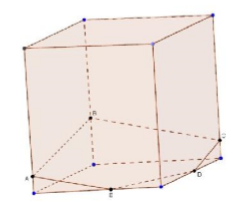
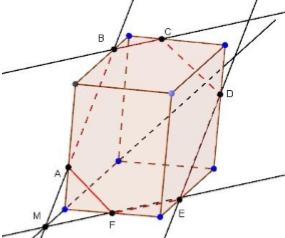
Решение: Построение искомого сечения зависит от того, на каких ребрах параллелепипеда лежат точки A, B и C. Рассмотрим некоторые частные случаи. Если точки A, B и C лежат на ребрах, выходящих из одной вершины, нужно провести отрезки AB, BC и CA, и получится искомое сечение–треугольник ABC. Если точки A, B и C расположены так, как показано на рисунке 6, то сначала нужно провести отрезки AB и BC, а затем через точку A провести прямую, параллельную AB. Пересечения этих прямых с ребрами нижней грани дают точки E и D. Остается провести отрезок ED, и искомое сечение–пятиугольник ABCDE–построено. Более трудный случай, когда данные точки A, B и C расположены так, как показано на рисунке 22. В этом случае можно поступить так, сначала построим прямую, по которой секущая плоскость пересекается с плоскостью нижнего основания. Для этого проведем прямую AB и продолжим нижнее ребро, лежащее в той же грани, что и прямая AB, до пересечения с этой прямой в точке M. Далее через точку M проведем прямую, параллельную прямой BC. Это и есть прямая, по которой секущая плоскость пересекается с плоскостью нижнего основания. Эта прямая пересекается с ребрами нижнего основания в точках E и F. Затем через точку E проведем прямую, параллельную прямой AB, и получим точку D. Наконец, проводим отрезки AF и CD, и искомое сечение –шестиугольник ABCDEF– построено.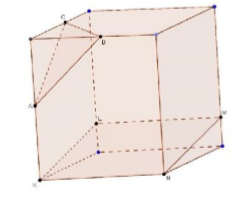

Заключение

Программа GeoGebra предназначена для обучения математике. С помощью этой программы можно работать в динамической математической среде, включающей в себя геометрию, алгебру и другие разделы, с широкими функциональными возможностями.

Использование программы GeoGebra на уроках позволяет:

– оптимизировать учебный процесс, более рационально используя время на различных этапах урока;

– осуществлять дифференцированный подход в обучении; - проводить индивидуальную работу, используя персональные компьютеры;

– снизить эмоциональное напряжение на уроке, внося в него элемент игры;

– расширять кругозор учащихся;

– способствует развитию познавательной активности учащихся.

Прогнозируемые эффекты от применения данной технологии:

– возможно повышение уровня самооценки;

– развитие навыка самоконтроля;

– побуждение к открытию и изучению нового в сфере информационных технологий, желанию поделиться с товарищами своими знаниями.

Список используемых источников

1. Иванчук, Н.В. Использование компьютерной программы GeoGebra на уроках математики в 7-11 классах: Методическое пособие / Н. В. Иванчук, О. В. Эйкен. – Мурманск: МГПУ, 2013.– 36 с.

2. Погорелов, А.В. Геометрия: Учеб. Для 7–11 кл. общеобразоват. учреждений.–9-е изд.–М.:Просвещение, 2014.

3. GeoGebra [Электронный ресурс]. — Режим доступа: https://ru.wikipedia. org/wiki/GeoGebra

4. Внеклассные мероприятия по информатике [Электронный ресурс]. — Режим доступа: http://www.uchportal.ru/programma-trenazhyor-po-matematike-obyknovennye-drobi

5. Живая геометрия [Электронный ресурс]. — Режим доступа: http://my-soft-blog.net/397-geogebra.html

6. Использование GeoGebra на уроках математики [Электронный ресурс]. — Режим доступа: hhttp://soft.mydiv.net/win/download-GeoGebra.htmlttp://s427.spb.ru/attachments/article/480/matem_spo.pdf