Построение СДНФ, СКНФ

Элементы математической логики

ТЕМА ЗАНЯТИЯ:

Б У Л Е В Ы Ф У Н К Ц И И. Совершенная дизъюнктивная нормальная форма (СДНФ).

Совершенная конъюнктивная нормальная форма (СКНФ).

ЦЕЛЬ ЗАНЯТИЯ:

НАУЧИТЬСЯ

Приводить высказывание

к СДНФ и СКНФ

устный опрос:

1. Дать определение ИНВЕРСИИ

2. Дать определение КОНЪЮНКЦИИ

3. Дать определение ДИЗЪЮНКЦИИ

4. Дать определение ИМПЛИКАЦИИ

5. Дать определение ЭКВИВАЛЕНЦИИ

6. Дать определение СУММЫ по модулю два

Построение таблицы истинности булевой функции для заданной формулы

Если х – логическая переменная,  {0, 1} – её значение в некотором наборе, то выражение

называется литерой .

Элементарной конъюнкцией называется конъюнкция попарно различных литер.

Пример 1: Имеется булева функция f(x 1 , x 2, x 3 , x 4 ) тогда элементарными конъюнкциями будут:

и так далее.

Построение таблицы истинности булевой функции для заданной формулы

Элементарной дизъюнкцией называется дизъюнкция попарно различных литер.

Пример 2: Имеется булева функция f(x 1 , x 2, x 3 , x 4 ) тогда элементарными конъюнкциями будут:

и так далее Замечание: в элементарную конъюнкцию (или дизъюнкцию) не обязаны входить все переменные!

правило вывода СДНФ

Пусть x 1 ,x 2, … , х n – набор переменных, (     ,..,  n )– набор значений переменных.

Конституентой единицы набора (     ,..,  n ) называется элементарная конъюнкция вида

К 1 (     ,..,  n ) =

Конституентой нуля набора (     ,..,  n ) называется элементарная дизъюнкция вида К 0 (     ,..,  n ) =

Замечание: обязательно входят все переменные!

правило вывода СДНФ

правило вывода СДНФ

Совершенной дизъюнктивной нормальной формой (СДНФ) называется дизъюнкция попарно различных конституент единицы.

Совершенной конъюнктивной нормальной формой (СКНФ) называется конъюнкция попарно различных конституент нуля.

правило вывода СДНФ

Алгоритм построения СДНФ:

• Выберем наборы значений переменных, на которых значение функции равно единице. (f=1);
• Для каждого такого набора построим Конституенту единицы ( отрицание входного нуля );
• Соединим конституенты единицы знаком дизъюнкции;
• При необходимости упростить.

правило вывода СКНФ

Алгоритм построения СКНФ:

• Выберем наборы значений переменных, на которых значение функции равно нулю. (f=0);
• Для каждого такого набора построим Конституенту нуля ( отрицание входной единицы);
• Соединим конституенты нуля знаком конъюнкции;
• При необходимости упростить.

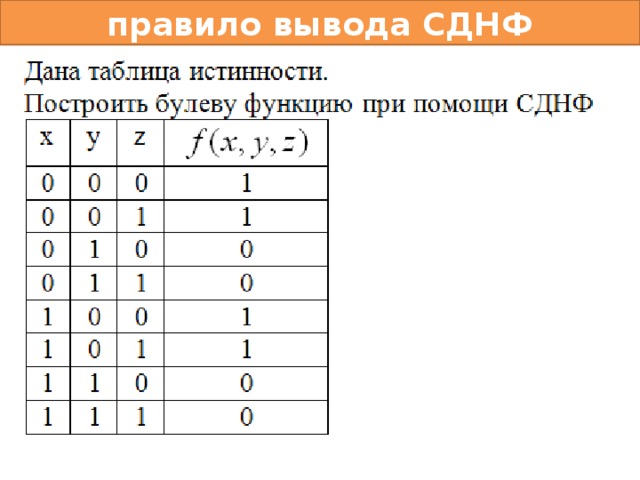
правило вывода СДНФ

правило вывода СДНФ

правило вывода СДНФ

правило вывода СДНФ

правило вывода СКНФ

правило вывода СКНФ

правило вывода СКНФ

правило вывода СКНФ

Построение таблицы истинности булевой функции для заданной формулы

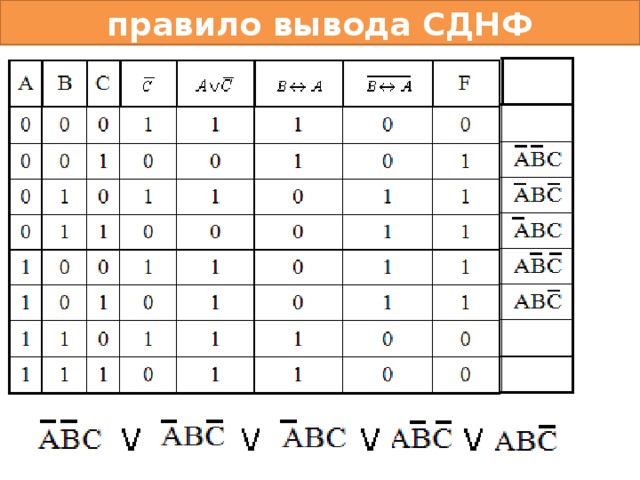
правило вывода СДНФ

правило вывода СДНФ

Алгоритм построения СДНФ:

• Выберем наборы значений переменных, на которых значение функции равно единице. (f=1);
• Для каждого такого набора построим отрицание входного нуля;
• Соединим наборы единицы знаком дизъюнкции;
• При необходимости упростить.

правило вывода СКНФ

Алгоритм построения СКНФ:

• Выберем наборы значений переменных, на которых значение функции равно нулю. (f=0);
• Для каждого такого набора построим отрицание входной единицы;
• Соединим наборы нуля знаком конъюнкции;
• При необходимости упростить.

Практическая часть

• Составить СДНФ функции, заданной таблицы истинности
• Составить СКНФ функции, заданной таблицей истинности для задания 1
• Составить таблицу истинности формулы высказываний
• Составить СДНФ функции, заданной таблицей истинности (задание 3)
• Составить СКНФ функции, заданной таблицей истинности (задание 3)