Поурочные планы по математике в 10 классе
На базе учебников : Колягин Ю. М., Сидоров Ю. В., Ткачева М.В., Шабунин М. И. «Алгебра и начала математического анализа 10». Профильный уровень. – М.: Мнемозина, 2006.» Учебник рекомендован Министерством образования и науки Российской Федерации.
«Геометрия: Учебник для 10-11 классов общеобразовательных учреждений
/ Атанасян Л.С.,. Бутузов В.Ф и др. – М.: Просвещение, 2007.»
Тема: ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ, ЕЕ СВОЙСТВА И ГРАФИК
Цели урока: Знать определение показательной функции, три основных свойства показательной функции, формировать умение строить графики показательных функций  , если
, если  или
или  ; развить умение читать графики функций, выделяя их свойства.
; развить умение читать графики функций, выделяя их свойства.
Некоторые наиболее часто встречающиеся виды трансцендентных функций, прежде всего показательные, открывают доступ ко многим исследованиям.
Л. Эйлер.
L Организационный момент.
П. Анализ контрольной работы и работа над ошибками. При проверке контрольной работы учитель делает ее анализ, отмечая все ошибки и недочеты, допущенные учащимися. Определяет наиболее часто встречающиеся ошибки. В соответствии с этим выстраивает работу над ошибками: подготавливает карточки с аналогичными заданиями для индивидуальной работы, тест для фронтальной работы (по наиболее типичным ошибкам). Например, учащиеся испытывали затруднения с преобразованием графиков.
ТЕСТ
1. С помощью каких пребразований получается график функции у = f^x) из графика функции у = g(x), если
д) f(x) = 2g(x) ж) f(x) = g(4x) з) f(x) = g(x/2)
a) f(x) = g(x) +3
б)f(x) = g(x)-2 е) f(x) = g(x)/ 3
в)f(x) = g(x+l)
r)f(x) = g(x-5)
Ответ: параллельный перенос вдоль:
а) оси Оу вверх на 3 единицы;
б) оси Оу вниз на 2 единицы;
в) оси Ох влево на 1 единицу;
г) оси Ох вправо на 5 единиц;
д) растяжение вдоль оси Оу в 2 раза;
е) сжатие вдоль оси Оу в 3 раза;
ж) сжатие вдоль оси Ох в 4 раза;
з) растяжение вдоль оси Ох в 2 раза.
2. Укажите, какой функции: а) у = (х - 2)2; б) у = х2 - 2;
в) у = (х + 2)2; г) у = (х - З)2 + 1; д) у = -х2 + 1; е) у = 4 - (х - З)2
соответствует график:
]) 2) 3)

3 -2 '3
Объясните почему. О т в е т: 1) - а); 2) - д); 3) - в); 4) - г); 5) - б); 6) - е).
К работе над ошибками нужно привлекать консультантов из | числа успевающих учеников.
III. Изучение нового материала.
1. Сравните формулы двух функций: у = х2 и у = 2х.
Первая - степенная, вторая - показательная. Подумайте, почему они так называются. Постройте их графики (показательную по точкам).

Попробуйте построить графики функции у = аx,если а = 3; 1/2; 1; -2. Сделайте вывод.
2. Функция вида у = аx, где а 0, а ≠ 1, называется показательной функцией. Она обладает следующими свойствами:
1) Область определения - множество R всех действительных чисел.
2) Область значений - множество всех положительных чисел.
3)Если а 1, то показательная функция возрастает, если 0 то убывает.
График показательной функции проходит через точку (0; 1) и расположен выше оси Ох.

3.№121-на доске по желанию.
Ответ: 1) 1,7; 2) 2,1; 3)0,6; 4)0,2.
№ 122(3,4)-за доской.
№124-устно.
Ответ: 1) 1.73 1; 2) 0,32 1,5 1,6; 4) 0,2 -3 0,2-2,
IV. Домашнее задание: № 122 (1, 2), № 125.
V. Итог урока. Приведите пример показательной функции. Является ли функция у = (-2)" показательной? Почему?
Математика 10 урок №____ дата_________________________
Тема: Показательная функция, ее свойства и график
Цели урока: закрепить навыки решения заданий на применение свойств показательных функций; формировать умение решать уравнения вида:  и неравенства вида
и неравенства вида  ,
,  развивающие: развивать навыки самоконтроля, взаимоконтроля, умения сравнивать, анализировать.
развивающие: развивать навыки самоконтроля, взаимоконтроля, умения сравнивать, анализировать.
воспитательные: воспитывать умения работать в паре, воспитывать культуру общения.
Ход урока:
Организационный момент.
Приветствие, сообщение темы и задач урока.
Проверка домашнего задания.
Учитель разбирает решение домашней работы, задавая вопросы по вариантам, только с теми, кто справился с домашней работой.
| Вариант 1 | Вариант 2 |
| 1. Опишите график функции, сравнивая с  или или  |
| 122(1) | №122 (2) |
| 2. Найдите наибольшее и наименьшее значения функций на промежутках:
 , ,  , ,  |
| 125 |
|
| 3. Назовите возрастающие функции | 3. Назовите убывающие функции |
Работа по карточкам.
Во время проверки домашней работы, учащиеся, не решавшие ее, работают по карточкам.
| Карточка 1 | Карточка 2 |
| 1. Дана функция  . Найдите наибольшее и наименьшее значения функции на отрезке . Найдите наибольшее и наименьшее значения функции на отрезке  . .
2. Найдите значение аргумента x, при котором функция 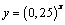 принимает значение, равное принимает значение, равное  . . | 1. Дана функция  . .
Найдите наибольшее и наименьшее значения функции на отрезке  . .
2. Найдите значение аргумента x, при котором функция  принимает значение, равное принимает значение, равное  . . |
| Карточка 3 | Карточка 4 |
| 1. Дана функция  . На каком отрезке данная функция принимает наибольшее значение, равное 25, наименьшее значение, равное 1? . На каком отрезке данная функция принимает наибольшее значение, равное 25, наименьшее значение, равное 1?
2. Сравните числа  и 1. и 1. | 1. Дана функция  . На каком отрезке данная функция принимает наибольшее значение, равное 17, наименьшее значение, равное3? . На каком отрезке данная функция принимает наибольшее значение, равное 17, наименьшее значение, равное3?
2. Сравните числа  и и  . . |
| Карточка 5 | Карточка 6 |
| 1. Дана функция  . Найдите координаты точки пересечения графика данной функции с графиком функции . Найдите координаты точки пересечения графика данной функции с графиком функции  . .
2. Исследуйте на монотонность функцию  . . | 1. Дана функция  . .
Найдите координаты точки пересечения графика данной функции с графиком функции  . .
2. Исследуйте на монотонность функцию  . . |
Объяснение нового материала.
Объяснение нового материала (стр. 43 -48):
1. Решение уравнений вида:  .
.
2. Решить уравнения:  ,
,  ,
,  ,
,  .
.
3. Решение неравенств вида:  и
и  .
.
4. Решить неравенства:  ,
,  ,
,  ,
,  .
.
5. Решить уравнение и неравенства:  ,
,  ,
,  .
.
Закрепление нового материала.
Решить задания из №127(1) - учитель с классом,
№127(3) – на доске по желанию
№ 128 – устно, № 130(1) – учитель с классом,
№ 130(2, 3, 4) – самостоятельно по вариантам,
№ 135 – устно,
№134(1, 3) –на доске по желанию,
№ 136(1) – учитель показывает на доске решение: у = 
№ 136(2, 3, 4) – работа в группах.
№ 138 – учитель с классом
Подведение итогов.
Домашнее задание: №127(2, 4); №134(2, 4); №137. теория в учебнике стр. 43-48.
Математика 10 урок №______ дата_________________________
Тема: Показательные неравенства
Цели урока: ввести понятие показательное неравенство; формировать умение решать показательные неравенства;
содействовать развитию логического мышления у учащихся, развивать умения анализировать, рассуждать, сравнивать, делать выводы, осмысливать материал;
воспитание познавательного интереса, элементов культуры общения, побуждать учащихся к преодолению трудностей в процессе умственной деятельности.
Ход урока:
Организационный момент.
Приветствие, сообщение темы и задач урока.
Математический диктант.
| Вариант 1 | Вариант 2 |
| Решите неравенства |
| 1) 2х = 4; 2) 2х =  ; ;
3)  = 81; 4) = 81; 4)  ; ;
5) 32х-4 =27; 6) . = =  | 1) 2х = 8; 2) 2х =  ; ;
3) ; 4) 0,2х = 0,04;
5) 54х+1 = 125; 6) 0,13х-9 = 0,001. |
Объяснение нового материала.
Объяснение нового материала - §8 (стр. 52-53): (презентация)
Показательное неравенство – это неравенство, содержащее неизвестное в показателе степени.
Решение неравенств:
а). Решение показательных неравенств часто сводится к решению неравенств ах ав (ах в ); если а1, то функция у = ах возрастает, и хв (х
Если 0 в)
 или
или  .
.
б). Некоторые показательные неравенства заменой ах = t сводятся к квадратным неравенствам, которые решают, учитывая, что t 0.
в) Графическое решение неравенства сводится к построению графиков функций из левой и правой частей неравенства. На интервале I большие (меньшие) значения принимает та функция, график которой расположен выше (ниже) графика другой функции.
3. Решить неравенства:  ;
;  ;
;  .
.
Закрепление нового материала.
5). Решить №156(1, 3)- на доске,
№ 157 – работа в группах;
№158(1) – учитель с классом,
№ 158(3) – на доске по желанию;
№ 158(2, 4) – самостоятельно по вариантам;
№ 166(1) – учитель показывает на доске решение;
№ 166(2,3,4) работа в группах
Домашнее задание: № 156(2, 4); 179(2, 4), тренажер №4
При изучении этой темы раздела «Показательная и логарифмическая функции», собирайте исторический материал, иллюстрации и интересные задачи по этой теме, которые вы можете в дальнейшем использовать на зачете.
Итог урока. Объясните алгоритм решения показательного неравенства. На что нужно обращать особое внимание?
Математика 10 урок №______ дата_________________________
Тема: Показательные неравенства
Цели урока: раскрыть содержание понятий «показательные неравенства» и «неравенства, сводящиеся к этому виду»; ознакомиться с основными приемами и методами решения неравенств этого вида; отработать навыки решения показательных неравенств основными методами.
Ход урока:
Организационный момент.
Приветствие, сообщение темы и задач урока.
Математический диктант.
Решение заданий по теме.

Так как a=141, то функция у=14t- возрастающая, то
х2+х ≤ 2;
х2+х-2≤ 0;
Пусть f(x)=x2+x-2 – квадратичная функция. Графиком является парабола, ветви направлены вверх, т.к. a=10. Найдем нули функции:
х2+х-2 = 0;
по теореме обратной теореме Виета имеем
 х1+х2=-1,
х1+х2=-1,
х1∙х2=-2;
х1= -2, х2=1.
Ответ: -2 ≤ х ≤ 1.
2).
Так как a=31, то функция у=3t – возрастающая, то
2х
x
Ответ: х
б) 0,36х-1- 0,36х≥ 0,7;
0,36х(0,3-1-1)≥0,7;

Так как 0a=0,3t- убывающая, то
6х ≤ 1;

Ответ: 
3).
32х+1-10∙3х+3
3∙32х-10∙3х+3
Пусть 3х= z, z0;
3z2-10z+3
Пусть f(x)=3z2-10z+3 – квадратичная функция. Графиком является парабола, ветви направлены вверх, т.к.a=30. Найдем нули функции:
3z2-10z+3=0;
 D=100-4∙3∙3=640;
D=100-4∙3∙3=640;
 z1=3, z2=
z1=3, z2=


3-1х
Так как a=31, то функция у=3t- возрастающая, то -1
Ответ: -1 x
4). 5х ≤ - х + 6; Решим неравенство графически. у= 5х – показательная функция,
у= - х + 6 – линейная функция, графиком является прямая.
Ответ: х ≥ 1.
Проверочная работа. Вариант 1
| Уровень  | Уровень | Уровень  |
| Решить неравенство: | Решить уравнение: | Решить систему |
| 1)  ; ;
2)  ; ;
3)  . . | 1)  ; ;
2) 
3)  . . | |
Вариант 2
| Уровень  | Уровень | Уровень  |
| Решить неравенство: | Решить уравнение: | Решить систему |
| 1)  ; ;
2)  ; ;
3)  . . | 1)  ; ;
2)  ; ;
3)  . . | |
Вариант 3
| Уровень  | Уровень | Уровень  |
| Решить неравенство: | Решить уравнение: | Решить систему |
| 1)  ; ;
2)  ; ;
3) . . | 1)  ; ;
2)  ; ;
3)  . . | |
Вариант 4
| Уровень  | Уровень | Уровень |
| Решить неравенство: | Решить уравнение: | Решить систему |
| 1)  ; ;
2)  ; ;
3)  . . | 1)  ; ;
2)  ; ;
3)  . . | |
Подведение итогов.
Домашнее задание: №189(2, 4); 190 (2); теория в учебнике стр. 51-53.
Математика 10 класс урок №____ дата____________________
Тема: Системы показательных уравнений.
Цели урока: повторить алгоритм решения систем уравнений способом подстановки, способом сложения; научить решать системы показательных уравнений;
Развитие логического мышления, зрительной памяти, математически грамотной речи, сознательного восприятия материала.
Воспитание познавательной активности, чувства ответственности, культуры общения.
Ход урока.
Организационный момент.
Повторение и закрепление знаний.
Учащиеся работают по карточкам.
Карточка № 1.
Изобразите схематически график функции у = 4х, опишите ее свойства.
2. Сравните числа: а) 1,73 и 1,75; б)  и
и  ; в)
; в) и
и  .
.
Решите уравнение: а) 3х-2 = 3; б) 3х-2 + 3х+1 =28; в) 9х - 6∙ 3х – 27 = 0.
Карточка № 2.
Решите уравнение: а) 0,5х = ; б) 25∙ 5х = 1; в) 4х = 9х.
; б) 25∙ 5х = 1; в) 4х = 9х.
Решите неравенство: а) 0,7х х - 4∙ 3х + 3 0.
Карточка № 3.
Решите уравнение: а)  =
=  ; б) 4х - 3х+2 = 7∙ 3х - 8∙ 22х.
; б) 4х - 3х+2 = 7∙ 3х - 8∙ 22х.
Решите неравенство: 4х +  -8 ≥ 0.
-8 ≥ 0.
Изучение нового материала.
Повторить алгоритм решения систем уравнений способом подстановки, способом сложения.
Определить, какие из систем уравнений решаются способом подстановки, какие – способом сложения.
Решить №240(1) способом подстановки, № 242(1) – способом сложения.(Алимов)
Система показательных уравнений сводится к системе линейных уравнений. Учитель показывает начало решения: ↔
…. Далее учащиеся решают самостоятельно. Ответ: х= 1; у = 3.
Учитель начинает решение, учащиеся продолжают:


 ….
….

.
 , b = 16х , тогда
, b = 16х , тогда





Перемножим уравнения системы:

5х  3у∙ 3х ∙ 5у = 15 ∙ 15; 15х+у = 152; х + у = 2 х = 2 – у и т.д.
3у∙ 3х ∙ 5у = 15 ∙ 15; 15х+у = 152; х + у = 2 х = 2 – у и т.д.
Домашнее задание.
Итог урока.
Дополнительные задания для сильных учащихся : № 244; 245 ( Алимов)
Математика 10 класс урок №____ дата____________________
Тема: Системы показательных неравенств.
Цели урока: повторить алгоритм решения систем показательных уравнений; научить решать систем показательных неравенств;
продолжить развитие таких познавательных процессов, как восприятие, внимание, память.
воспитывать устойчивый познавательный интерес к предмету ;
воспитывать такие качества личности, как активность, самостоятельность и аккуратность в работе;
Ход урока.
Организационный момент.
Проверка знаний учащихся.
Самостоятельная работа(15 – 20 мин.)
Вариант 1. Вариант 2.
Изобразите схематически график функции:
у = 2,3х у = 0,7х
Сравните числа:
 и
и 
 и
и 
Решите уравнение:
 = 4,5х-2 9х = 27
= 4,5х-2 9х = 27
Решите неравенство:
 8
8 
Решите систему уравнений:
Решение заданий.
№ 160(1) – учитель с классом
№ 160(2) – на доске по желанию.
№ 155( 1) – учитель с классом;
№ 155(3, 5) – на доске по очереди;
№ 244(1, 2) (Алимов) – на доске;
Домашнее задание: изучить § 7, 8 ; решить №155(2, 4, 6); № 160(2, 4).
Итог урока.
Дополнительное задание. № 187, 188.
Математика 10 класс урок №____ дата____________________
Тема: Системы показательных уравнений и неравенств.
Цели урока:
повторить алгоритм решения систем уравнений способом подстановки, способом сложения;
закрепить навыки решения системы показательных уравнений и неравенств;
развивать вкус к исследованию и поиску зависимостей;
воспитывать устойчивый познавательный интерес к предмету математика через показ практического применения темы;
воспитывать такие качества личности, как активность, самостоятельность и аккуратность в работе.
Ход урока.
Организационный момент.
Анализ самостоятельной работы.
Повторение и закрепление знаний.
Изобразить график показательной функции при а 1 и при 0
Чем отличаются графики функций у = ах и у = а-х?
Работа с графическим лото. Учащимся выдается карта и набор карточек. Задание – определить, какой функции соответствует график.
Набор карточек:
у = 2х+1 2) у = 2х 3) у = 2х – 1 4) у = 2-х 5) у = 
у = 21-х + 3 7) у =  8) у = 2х + 1 9) у = 21-х 10) у =
8) у = 2х + 1 9) у = 21-х 10) у =  + 1.
+ 1.
Построить график функции у = 4х – 2х+1.(1 ученик)
Исследование:
Исследуйте вспомогательную функцию g(t) = t2 – 2t при t 0, определив:
промежутки постоянного знака;
корни;
область значений;
промежутки монотонности.
Исследуйте данную функцию, используя результаты предыдущего пункта.
Постройте график функции у = 4х – 2х+1.
Ответ:

5). Исследовательская работа.(1 ученик).
Функция f(x) =  .
.
Выразите f(x) как функцию от t, где t = 2х.
Исследуйте вспомогательную функцию у = при t 0.
при t 0.
Найдите область значений функции у = f(x).
Постройте график функции у = f(x).
Решите уравнение f(x) =  .
.
Решите неравенство f(x) ≤  .
.
При каких значениях а уравнение f(x) = а имеет 2 корня.
Ответ: 1) f(t)  . 2) D(f); t 0; корней нет; у 0 при t 0. 3) (0; 0,5].
. 2) D(f); t 0; корней нет; у 0 при t 0. 3) (0; 0,5].
5) х1 = 1; х2 = -1. 6) х ≤ -2, х ≥ 2. 7) а Є (0;0,5).

Домашнее задание: № 195(2,4); 526(1); 193(2,4).
Итог урока. Учащиеся сами анализируют свои работы.
Использованы материалы пособия для учителя «Алгебра и начала анализа. 10 класс» Авт.-сост. Г.И.Григорьева, ресурсы Интернет.



















