Практическая работа №1 «Построение узора из окружностей»
Цели работы:
-
Знакомство с геометрическими фигурами - окружность и круг.
-
Изучение элементов окружности.
-
Измерение радиусов окружности и круга.
-
Построение окружности и круга.
-
Построение узора из окружностей.
Оборудование: циркуль, линейка, карандаш.
Ход работы
П ознакомьтесь с алгоритмом построения окружности и изучите ее свойства.
ознакомьтесь с алгоритмом построения окружности и изучите ее свойства.
1.Поставьте на листе тетради точку. Обозначь ее буквой О.
2.Возьмите циркуль в руки следующим образом: ножку циркуля с иглой установи в точку О, а ножку циркуля с грифелем вращайте вокруг данной точки, касаясь листа тетради. Циркуль опишет замкнутую линию. Ее называют окружностью. Точку О называют центром окружности.
3.Отметьте точку А на окружности и проведите отрезок, соединяющий точку А и центр окружности точку - О, такой отрезок называется радиус.
4.Постройте радиус ОВ.
| № | Радиус (обозначение отрезка) | Длина |
-
| ОА |
|
-
| ОВ |
|
Ответьте на вопросы и выполните задание:
-
Сколько радиусов можно провести в одной окружности?
-
Сравните длины этих отрезков.
-
Сделайте вывод, запишите его в тетрадь.
5.Постройте отрезок МК, соединяющий две точки окружности, который проходит через её центр, такой отрезок называется диаметр.
6.Построй диаметр РТ.
| № | Диаметр (обозначение отрезка) | Длина |
-
| МК |
|
-
| РТ |
|
Ответьте на вопросы и выполните задание:
-
Сколько диаметров можно провести в одной окружности?
-
С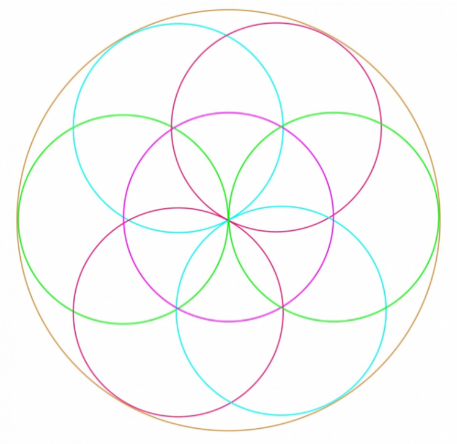 равните длину диаметра с длиной радиуса.
равните длину диаметра с длиной радиуса.
-
Сделайте вывод.
-
Запишите вывод в тетрадь.
7.Нарисуйте окружность. Не меняя радиуса, переставьте ножку циркуля с иглой в любую точку на окружности и снова нарисуйте окружность. Точки пересечения этих окружностей станут центрами новых окружностей. Внутри основного круга появился цветок.
Контрольный вопрос:
Что можно сказать о расположении точек окружности по отношению к центру окружности?
Дополнительные вопросы и задания:
1.Нарисуйте две окружности, которые не пересекаются. Измерьте длины их радиусов, расстояние между их центрами и сделай вывод. Запишите вывод в тетрадь.
2.Нарисуйте две окружности, которые пересекаются в двух точках. Измерьте длины их радиусов, расстояние между их центрами и сделай вывод. Запишите вывод в тетрадь.
3.Нарисуйте две окружности, которые имеют одну общую точку. Измерьте длины их радиусов, расстояние между их центрами и сделай вывод. Запишите в тетрадь.
4.Приведите примеры окружности и круга в окружающих вас предметах.
Практическая работа №1 «Построение узора из окружностей»
Цели работы:
-
Знакомство с геометрическими фигурами - окружность и круг.
-
Изучение элементов окружности.
-
Измерение радиусов окружности и круга.
-
Построение окружности и круга.
-
Построение узора из окружностей.
Оборудование: циркуль, линейка, карандаш.
Ход работы
П ознакомьтесь с алгоритмом построения окружности и изучите ее свойства.
ознакомьтесь с алгоритмом построения окружности и изучите ее свойства.
1.Поставьте на листе тетради точку. Обозначь ее буквой О.
2.Возьмите циркуль в руки следующим образом: ножку циркуля с иглой установи в точку О, а ножку циркуля с грифелем вращайте вокруг данной точки, касаясь листа тетради. Циркуль опишет замкнутую линию. Ее называют окружностью. Точку О называют центром окружности.
3.Отметьте точку А на окружности и проведите отрезок, соединяющий точку А и центр окружности точку - О, такой отрезок называется радиус.
4.Постройте радиус ОВ.
| № | Радиус (обозначение отрезка) | Длина |
-
| ОА |
|
-
| ОВ |
|
Ответьте на вопросы и выполните задание:
-
Сколько радиусов можно провести в одной окружности?
-
Сравните длины этих отрезков.
-
Сделайте вывод, запишите его в тетрадь.
5.Постройте отрезок МК, соединяющий две точки окружности, который проходит через её центр, такой отрезок называется диаметр.
6.Построй диаметр РТ.
| № | Диаметр (обозначение отрезка) | Длина |
-
| МК |
|
-
| РТ |
|
Ответьте на вопросы и выполните задание:
-
Сколько диаметров можно провести в одной окружности?
-
С равните длину диаметра с длиной радиуса.
равните длину диаметра с длиной радиуса.
-
Сделайте вывод.
-
Запишите вывод в тетрадь.
7.Нарисуйте окружность. Не меняя радиуса, переставьте ножку циркуля с иглой в любую точку на окружности и снова нарисуйте окружность. Точки пересечения этих окружностей станут центрами новых окружностей. Внутри основного круга появился цветок.
Контрольный вопрос:
Что можно сказать о расположении точек окружности по отношению к центру окружности?
Дополнительные вопросы и задания:
1.Нарисуйте две окружности, которые не пересекаются. Измерьте длины их радиусов, расстояние между их центрами и сделай вывод. Запишите вывод в тетрадь.
2.Нарисуйте две окружности, которые пересекаются в двух точках. Измерьте длины их радиусов, расстояние между их центрами и сделай вывод. Запишите вывод в тетрадь.
3.Нарисуйте две окружности, которые имеют одну общую точку. Измерьте длины их радиусов, расстояние между их центрами и сделай вывод. Запишите в тетрадь.
4.Приведите примеры окружности и круга в окружающих вас предметах.






 ознакомьтесь с алгоритмом построения окружности и изучите ее свойства.
ознакомьтесь с алгоритмом построения окружности и изучите ее свойства. равните длину диаметра с длиной радиуса.
равните длину диаметра с длиной радиуса.





















