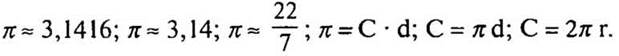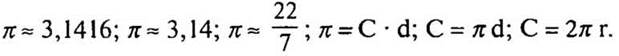Практическая работа

 Практическая работа.

а) Мне нужны два помощника.

— Возьмем круглый предмет и обведем его мелом на доске, а вы у себя в тетради обведите модели кругов. На доске и у вас в тетрадях получится окружность.

— Что такое окружность? (Замкнутая линия. Все точки окружности одинаково удалены от ее центра.)

— Возьмем нитку, обмотаем ее вокруг нашего стакана (цилиндра, подставки для карандашей, ручки), а потом распрямим нить.

— Длина нити будет приближенно равна длине нарисованной окружности.

— Проверим. Обмотайте нить по нарисованной в тетради окружности. Попросите помощи у товарища.

 Измерьте, чему равна длина вашей окружности.

— Как это сделать? (Измерить длину нити.)

б) Начертите с помощью циркуля окружность.

— Центр окружности обозначим точкой О.

— Дайте определение окружности. (Все точки находятся на одинаковом расстоянии от центра окружности.)

— Выберите любую точку на окружности. Обозначим ее А.

— Как называется отрезок ОА? (Радиус.)

— Постройте еще одну окружность.

— Проведите отрезок, проходящий через центр окружности.

— Как он называется? (Диаметр.)

— Чему равен диаметр? (Он в 2 раза больше радиуса.)

— Диаметр в переводе с греческого слова означает «поперечник». У древнегреческих математиков слово употреблялось и в значении «диагональ».

— С помощью нити измерьте длину окружности.

— Измерьте длину диаметра.

(Записать на доске несколько вариантов измерений.)

3. Работа над новой темой.

— Какой вывод можно сделать? (Длина окружности прямо пропорциональна длине ее диаметра.)

— Найдите отношение длины окружности к длине ее диаметра. (Можно воспользоваться микрокалькулятором.)

— Какое число у вас получилось? (Бесконечная десятичная дробь.)

(Записать на доске ответы детей.)

— Округлите ее до тысячных, до сотых, до десятых, до единиц.

— Что интересного заметили? (Хотя окружности были построены у всех разные, отношения длины окружности к диаметру получились примерно одинаковые.)

— Какой вывод можно сделать? (Отношение длины окружности к длине ее диаметра является одним тем же числом.)

По ходу объяснения записывать на доске и в тетрадь.

— Это число обозначают греческой буквой ж.

— Подсчеты показали, что с точностью до десятитысячных π ≈ 3,1416.

— Запоминание величины π (3,1416) связывают с предложением «Что я знаю о круге», где количество букв в каждом слове равно соответствующей цифре числа п.

— Округлите это значение до сотых: 3,1416.

— Читают: «Пи приближенно равно трем целым четырнадцати сотым».

— Примерно такую же точность дает значение π ≈ 22/7.

— В старших классах вы узнаете, как проводились такие расчеты. Число 22/7 носит имя великого математика: называется оно «число Архимеда».

— Обозначим длину окружности буквой С, а длину диаметра буквой d.

— Вспомним, как мы находили π. π = С · d.

— Выразим из этой формулы С: С = πd.

— Так как d = 2r, то по-другому можно записать формулу длины окружности: С = 2πr.

Записи в тетради: