Практическая работа по теме "Построение треугольника с помощью циркуля и линейки "

7А. Геометрия

ТЕМА: «Построение с помощью циркуля и линейки»

УМК: Бутузов

Заранее попросить подготовить ученика доклад об истории геометрического построения циркулем и линейкой.

Например,

Традиционное ограничение орудий геометрических построений восходит к глубокой древности. В своей книге "Начала" Евклид (III век до н. э.) строго придерживается геометрических построений, выполняемых циркулем и линейкой, хотя названий инструментов он нигде не упоминает. Ограничения, по-видимому, были связаны с тем, что эти инструменты заменили собой веревку, первоначально служившую как для проведения прямых, так и для описания окружностей. Но многие историки-математики объясняют произведенный Евклидом отбор материала тем, что он, следуя Платону и пифагорейцам, считал только прямую и круг "совершенными" линиями.

Искусство построения геометрических фигур было в высокой степени развито в Древней Греции. Древнегреческие математики еще 3000 лет назад проводили свои построения с помощью двух приборов: гладкой дощечки с ровным краем – линейки и двух заостренных палок, связанных на одном конце – циркуля. Однако этих простейших инструментов оказалось достаточно для выполнения огромного множества различных построений. Древним грекам даже казалось, что любое разумное построение можно совершить этими инструментами, пока они не столкнулись с тремя знаменитыми впоследствии задачами.

Они издавна преобразовывали любую прямолинейную фигуру с помощью циркуля и линейки в произвольную прямолинейную фигуру, равновеликую ей. В частности, всякая прямолинейная фигура преобразовывалась в равновеликий ей квадрат. Поэтому понятно, что появилась мысль обобщить эту задачу: построить с помощью циркуля и линейки такой квадрат, площадь которого была бы равна площади данного круга. Это задача получила название квадратуры круга. Следы этой задачи можно усмотреть еще в древнегреческих и вавилонских памятниках второго тысячелетия до н.э. Однако ее непосредственная постановка встречается в греческих сочинениях V века до н.э.

Еще две задачи древности привлекали внимание выдающихся ученых на протяжении многих веков. Это задача об удвоении куба. Она состоит в построении циркулем и линейкой куба, имеющего объем вдвое больший, чем объем данного куба. Ее появление связывают с легендой, что на острове Делос в Эгейском море оракул, чтобы избавить жителей от эпидемии чумы, повелел удвоить алтарь, имевший форму куба. И третья задача трисекции угла о делении угла на три равные части с помощью циркуля и линейки

Эти три задачи, так называемые 3 знаменитые классические задачи древности, привлекали внимание выдающихся математиков на протяжении двух тысячелетий. И лишь в середине XIX века была доказана их неразрешимость, то есть невозможность указанных построений лишь с использованием только циркуля и линейки. В математике это были первые результаты о неразрешимости задач, когда средства решения указаны. Они были получены средствами не геометрии, а алгебры (с помощью перевода этих задач на язык уравнений), что еще раз подчеркнуло единство математики. Не поддаваясь решению, эти проблемы обогатили математику значительными результатами, привели к созданию новых направлений математической мысли.

Еще одной интереснейшей задачей на построение с помощью циркуля и линейки является задача построения правильного многоугольника с заданным числом сторон. Древние греки умели строить правильный треугольник, квадрат, правильные пятиугольник и 15-угольник, а также все многоугольники, которые получаются из них путем удвоения сторон, и только их. Лишь в 1796 году великий немецкий математик К.Ф.Гаусс открыл способ построения правильного 17-угольника при помощи циркуля и линейки и указал все значения N, при которых возможно построение правильного N-угольника указанными средствами. Первокурсник Геттингенского университета Карл Гаусс решил задачу, перед которой математическая наука пасовала более 2 с лишним тысяч лет. Таким образом, была доказана невозможность построения с помощью циркуля и линейки правильных 7, 9, 11, 13, 18, 21, 22, 23 и т.д. угольников.

Теория построения при помощи циркуля и линейки получила свое дальнейшее развитие. Был получен ответ на вопрос: можно ли решить задачу с помощью только одного из двух рассматриваемых инструментов, и достаточно неожиданный. Независимо друг от друга, датчанин Г.Мор в 1672 году и итальянец Л.Маскерони в 1797 году доказали, что любая задача на построение, разрешаемая циркулем и линейкой, может быть точно решена с помощью только одного циркуля. Это кажется невероятным, но это так. А в XIX веке было доказано, что любое построение, выполняемое с помощью циркуля и линейки можно провести лишь с помощью одной линейки, при условии, что в плоскости построения задана некоторая окружность и указан ее центр.

С какими видами геометрических задач сталкивались уже? (На доказательство, анализ, исследование и тд)

Есть еще 1 вид – задачи на построение. Когда Вы анализируете задачу, необходимо представить все построения и рассмотреть все возможные случаи на чертеже.

Какие инструменты используете для построения? (Линейка, транспортир, циркуль, угольник)

Что можно построить с помощью линейки? (прямую, проходящую через 2 данные точки)

А с помощью циркуля? (окружность с центром в данной точке и радиусом, равным данному отрезку)

Многие фигуры можно построить только с помощью циркуля и линейки. Итак, тема сегодняшнего урока…

Задачи на построение – алгоритм построения отрезков, треугольников, многоугольников, углов и тд

Давайте попробуем составить эти алгоритмы.

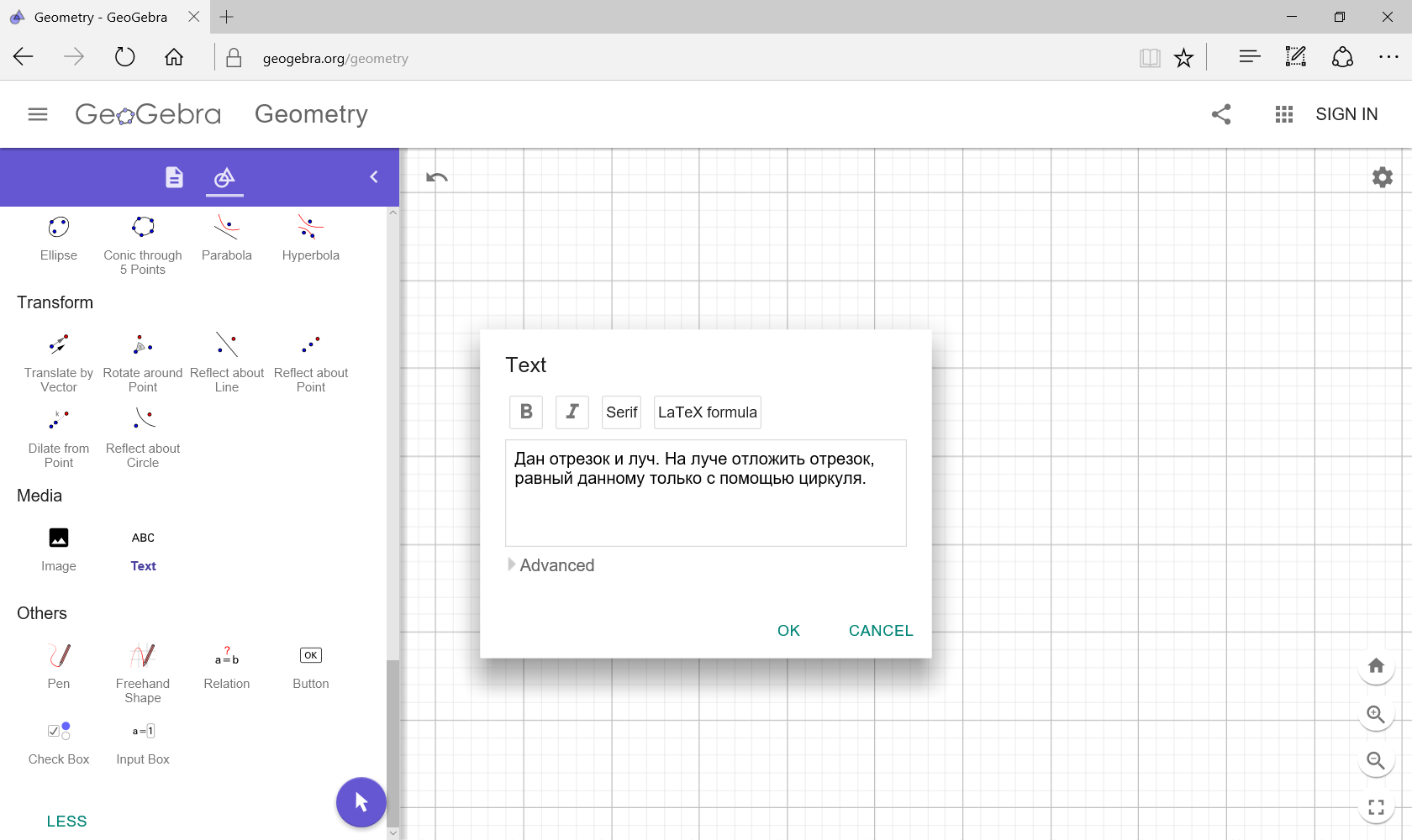
Задача 1. Дан отрезок и луч. На луче отложить отрезок, равный данному с помощью линейки.

Задача 2. Изменим условие задачи 1 и построим отрезок только с помощью циркуля.

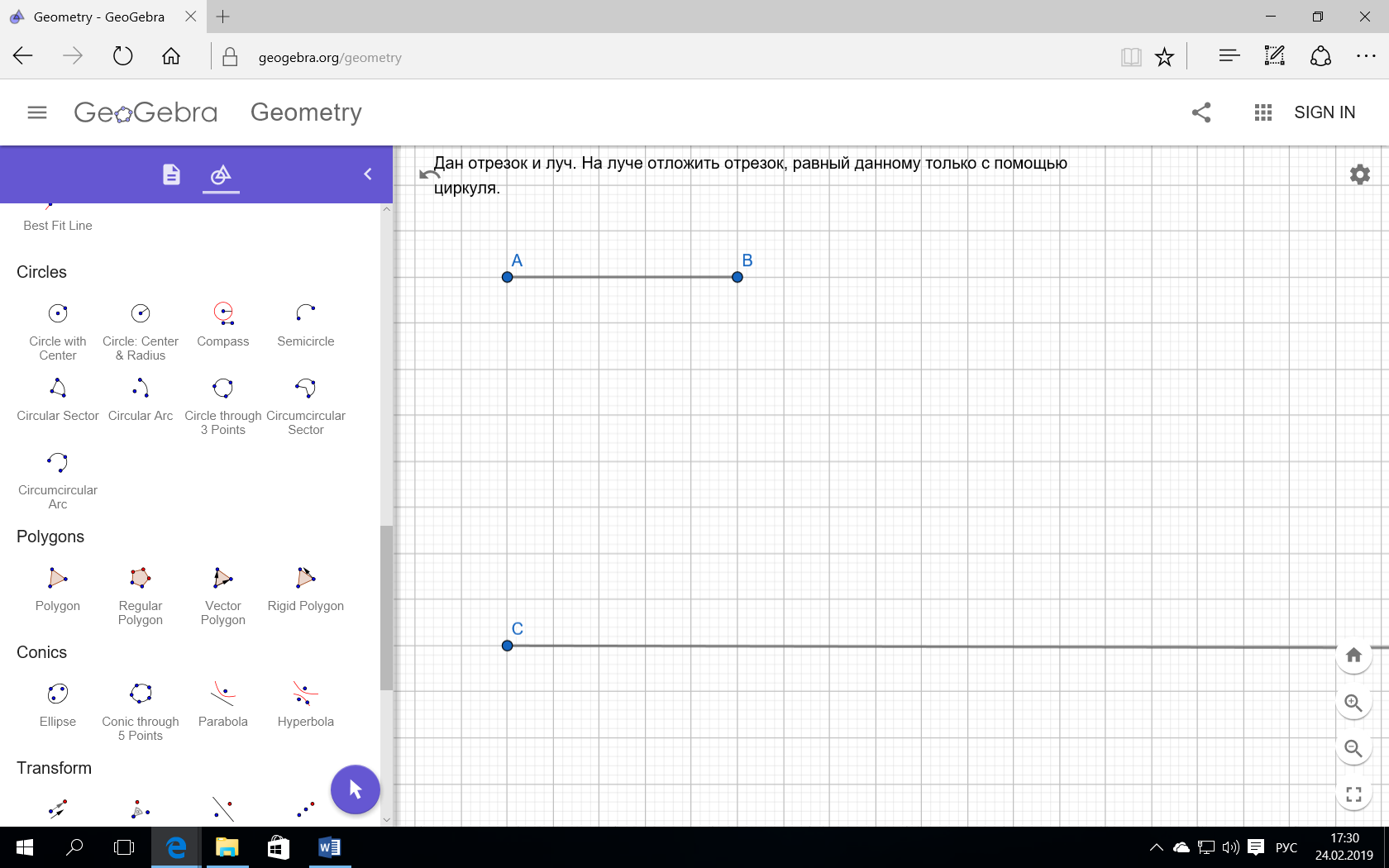
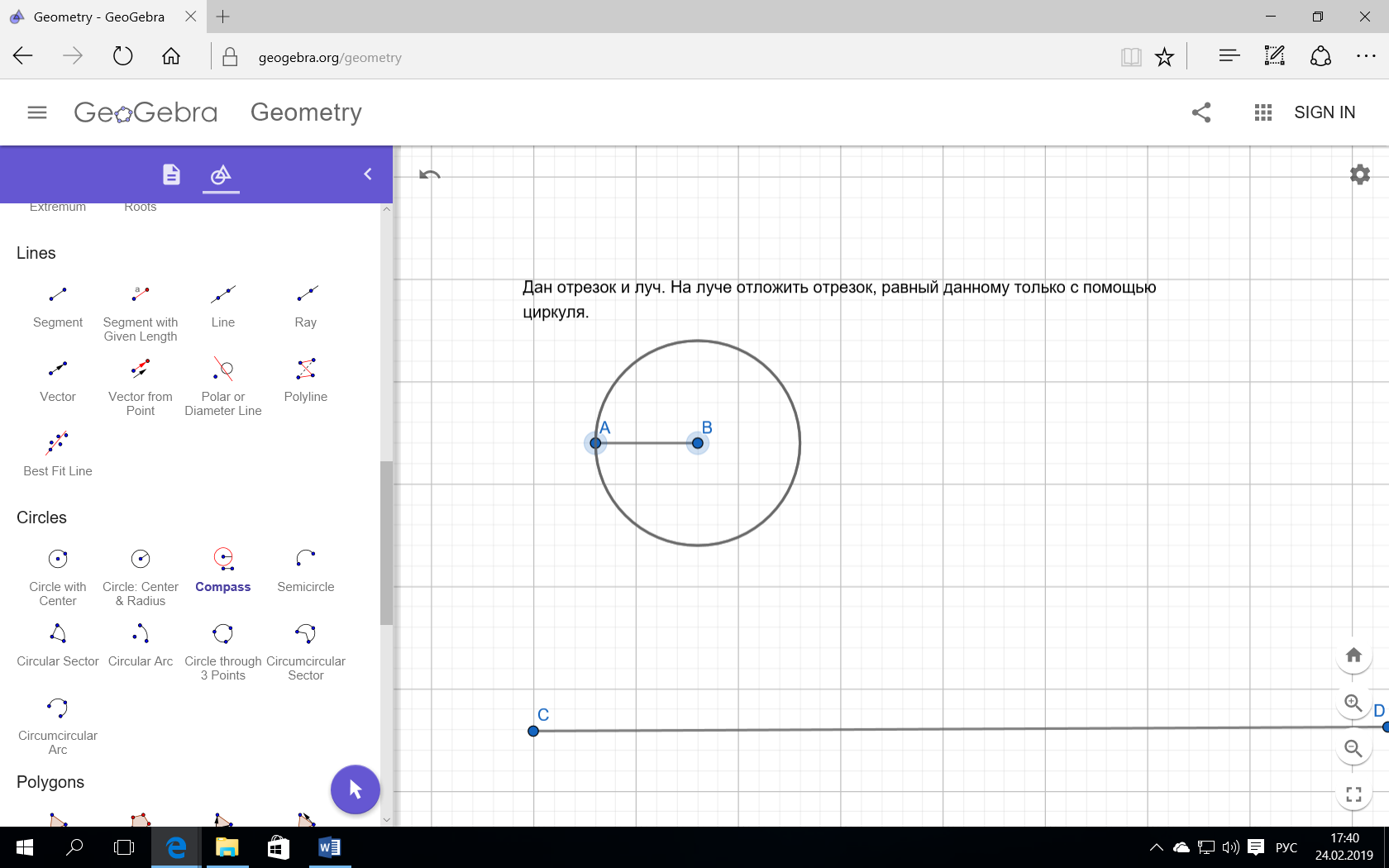
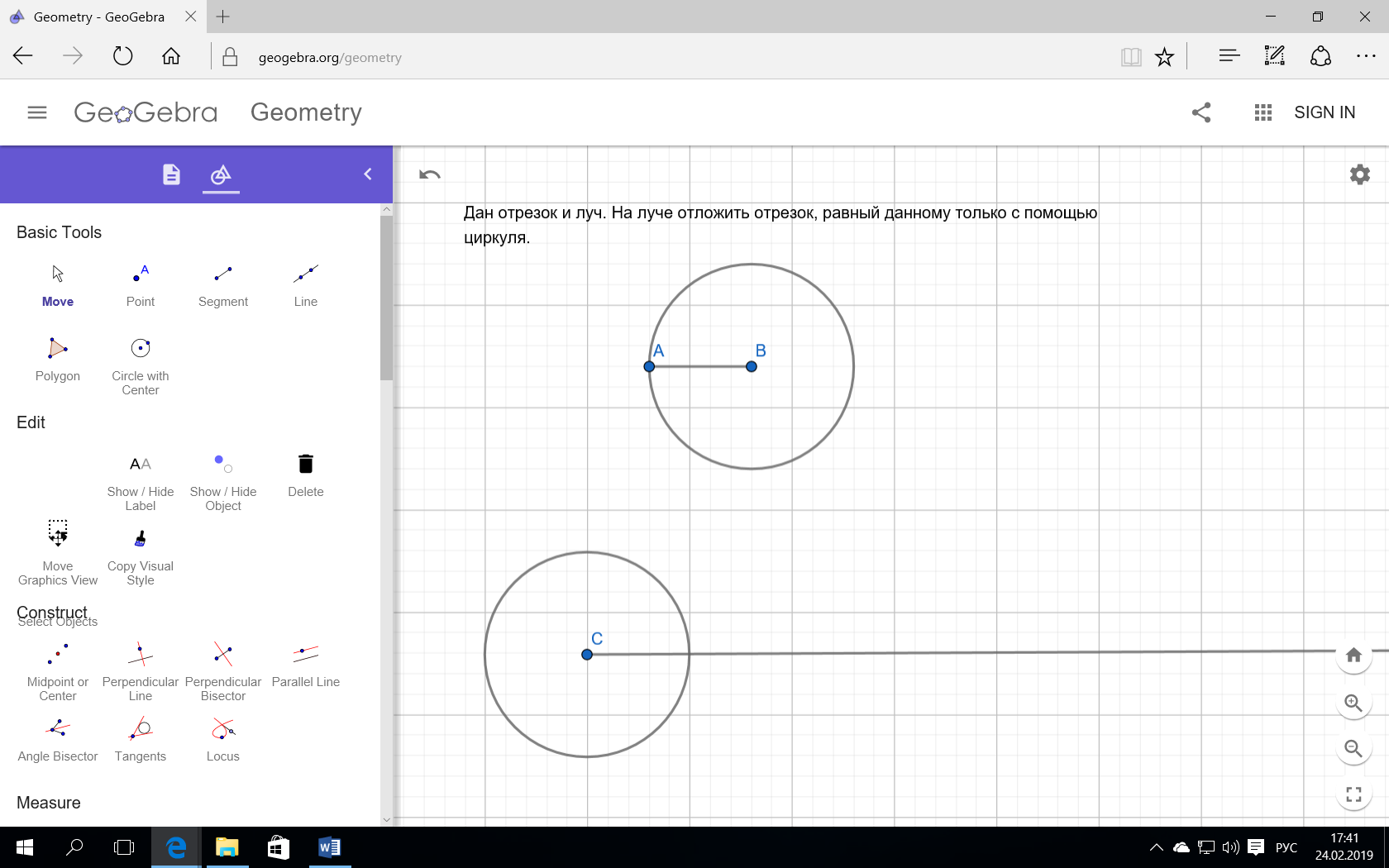
Отметим точку и получим отрезом СD=AB

Алгоритм: …

Замечание: не обязательно строить окружность. Достаточно сделать пометки.

Самостоятельна задача. Аналогично задаче 2. Взять другие отрезки, например

Задача 3. Построить треугольник АВС по трем сторонам.

Что дано? Что требуется?

Пусть даны отрезки А’В’, A’C’, B’C’.

Т е требуется построить треугольник, стороны соответственно равны 3м отрезкам:

А’В’=AB, A’C’=AC, B’C’=BC.

1. Возьмем некий луч и аналогично предыдущий задаче отложим, например, А’В’=AB.

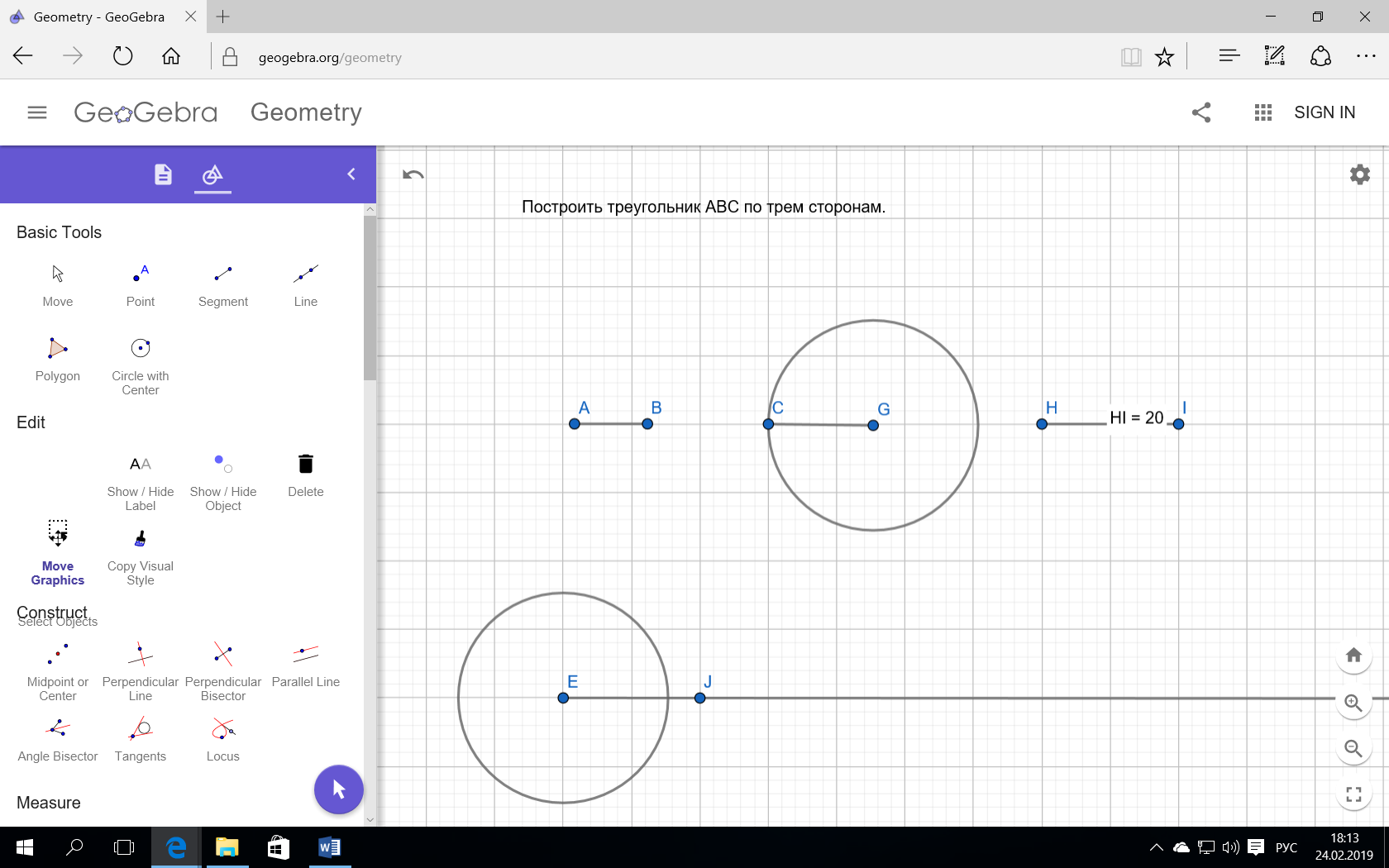
2. Построим окружность радиуса A’C’ от т.А

3. Аналогично сделаем относительно B’C’ и т.В

Обозначения другие!

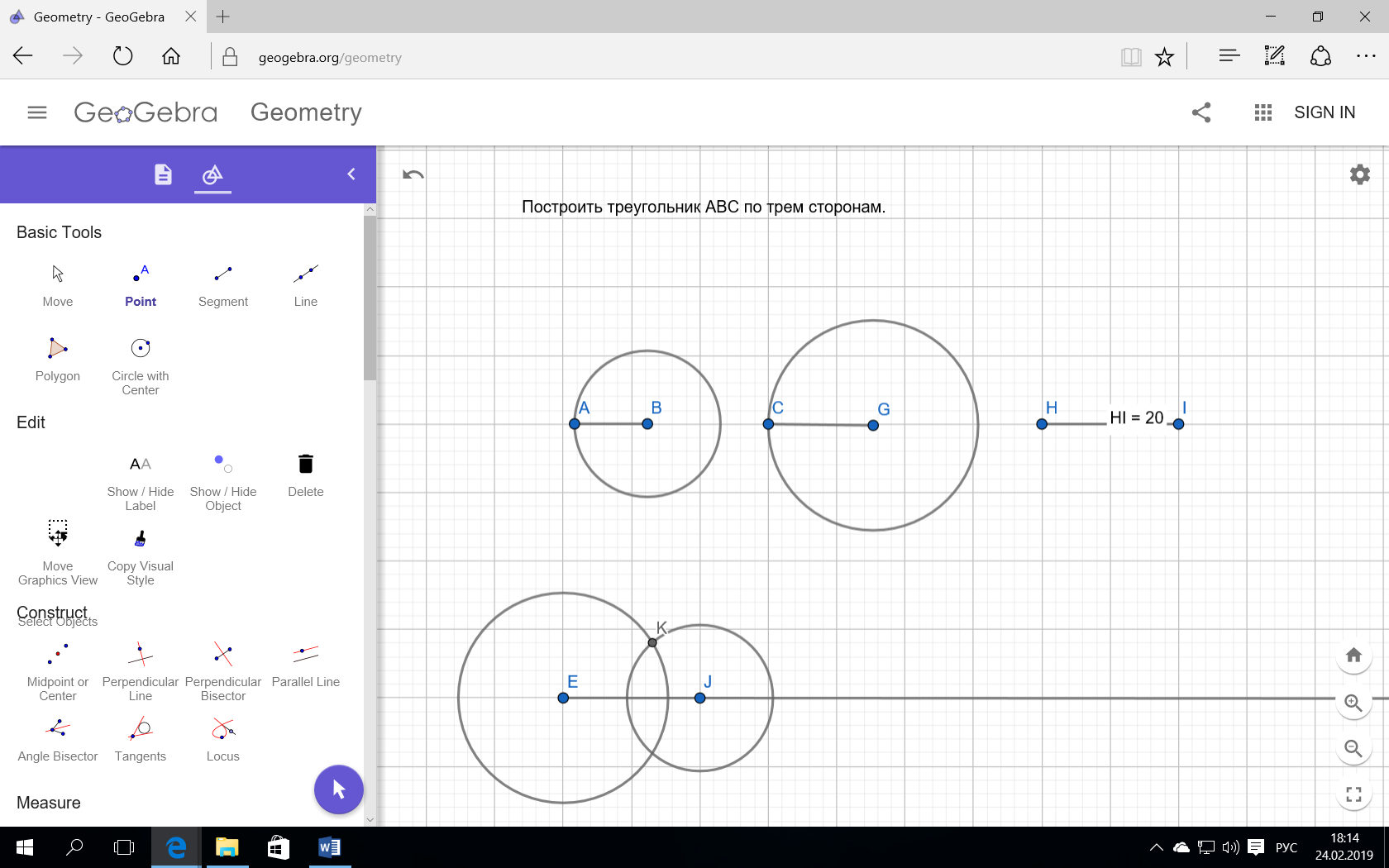
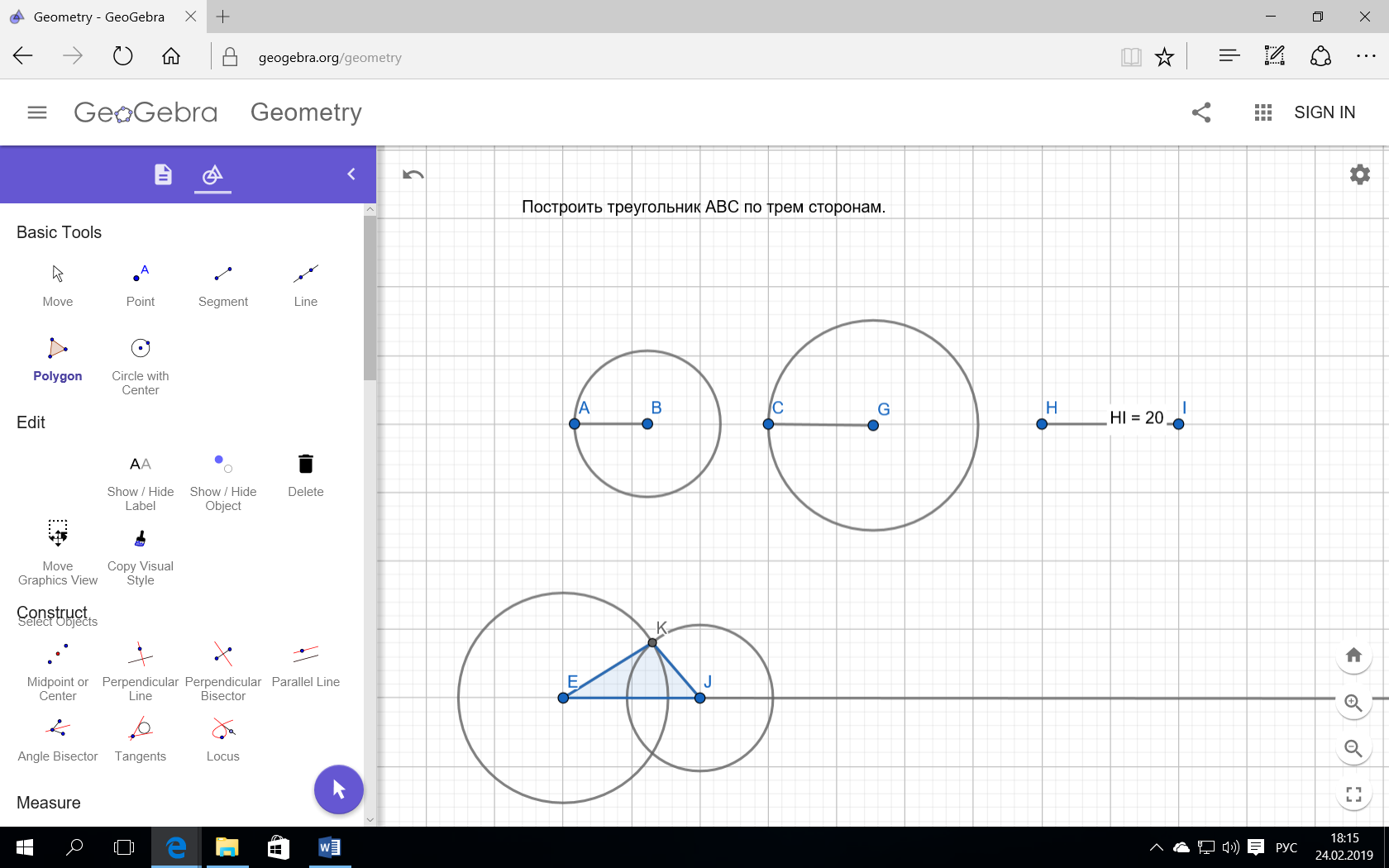
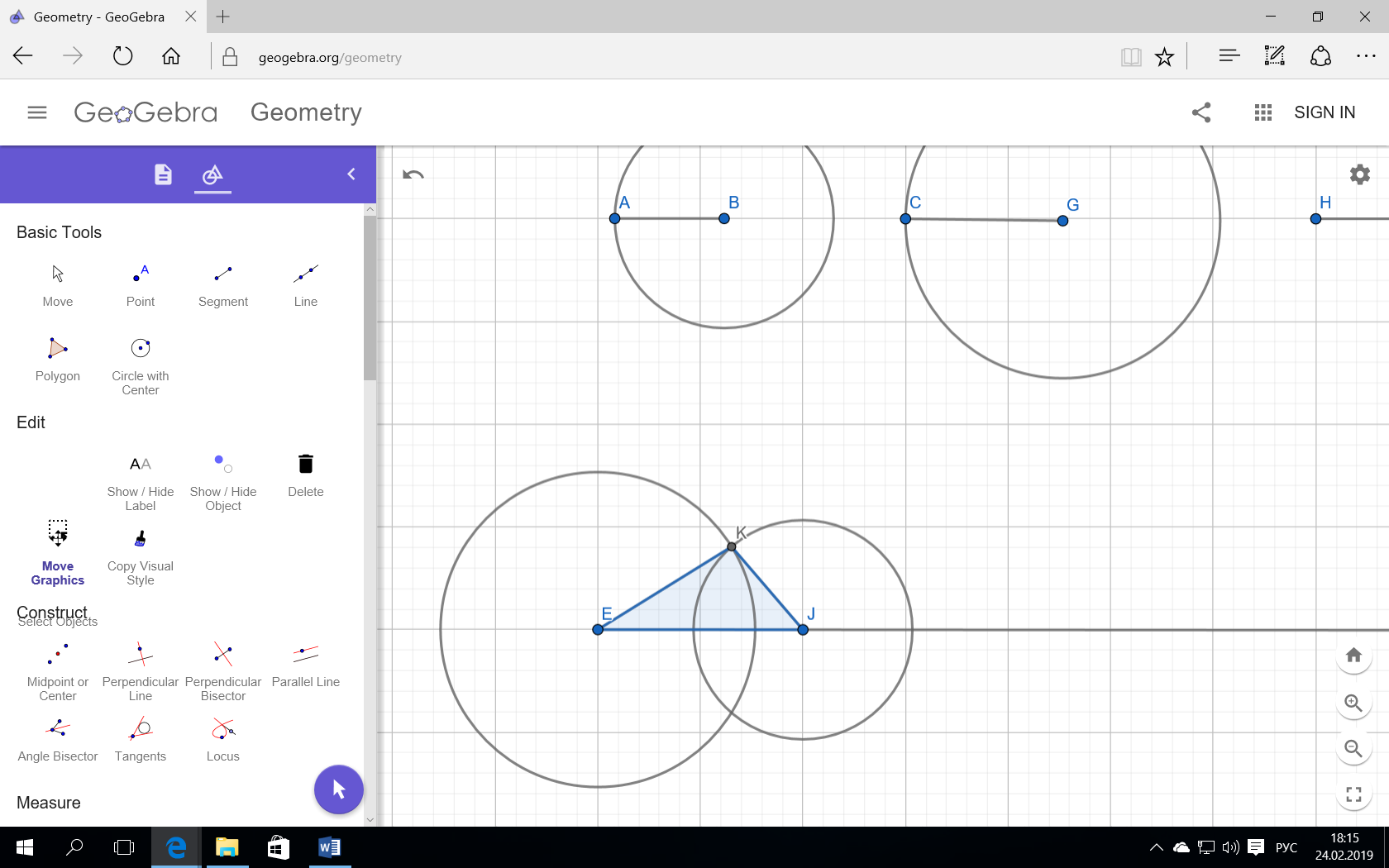
Если если поменяем порядок? Например, отложим не АВ, а ВС или АС. Изменится ли что то? Если да, то что?

В каком случае вообще можно построить треугольник?

Задача 4 и 5. Лабораторная работа. 1 вариант – работает с равнобедренным треугольником, 2й – с равносторонним.

А если требуется построить равнобедренный треуг? Какие условия должны быть даны?

Аналогично с равносторонним. Условия (отрезки) задать самостоятельно.

Ученики обмениваются знаниями. Рассмотрим данные треугольники (возьмем р-б). опустим перпендикуляр. Вспомним свойства р-б треугольника. Значит, данный перпендикуляр разбивает отрезок пополам. Мы разбили отрезок только с помощью циркуля.

Итак, чему мы научились?
какие треугольники научились строить?

ДЗ. Построить соединенные фигуры, используя построения отрезка, треугольника, в том числе р-б, р-ст, разбиение отрезка пополам.