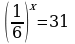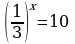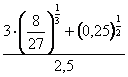СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 26.05.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

Практические работы по математике для профессии СПО "Мастер общестроительных работ"
Практические работы по математике для студентов СПО
Просмотр содержимого документа
«Практические работы по математике для профессии СПО "Мастер общестроительных работ"»
Практическая работа №1.
Действия с рациональными числами.
Цели: отработать навык выполнения вычислений с действительными числами.
Оборудование: тетрадь для практических работ, ручка, методические рекомендации по выполнению работы
Указание. Практическая работа состоит из двух частей – теоретической и практической. После изучения теоретического материала можно приступать к выполнению практической части. Она состоит из одной или более задач для самостоятельного выполнения. Не забывайте о правильном оформлении решения
Порядок выполнения работы.
-
Рассмотрите теоретический материал по теме и примеры решения задач (приведены ниже).
-
Решите самостоятельную работу. Оформите решение письменно в тетради.
Ход работы.
Теоретический материал.
Правило перевода периодической десятичной дроби в обыкновенную. 



| Количество баллов за задание |
| 2 |
| 2 |
| 2 |
| 1 |
| 4 |
| 4 |
1 вариант

2 вариант
| Количество баллов за задание |
| 2 |
| 2 |
| 2 |
| 1 |
| 4 |
| 4 |

Практическая работа 2.
Решение задач
Цели: закрепить умения и навыки выполнения действий с обыкновенными и десятичными дробями.
Оборудование: тетрадь для практических работ, ручка, методические рекомендации по выполнению работы
Указание. Практическая работа состоит из двух частей – теоретической и практической. После изучения теоретического материала можно приступать к выполнению практической части. Она состоит из одной или более задач для самостоятельного выполнения. Не забывайте о правильном оформлении решения
Порядок выполнения работы.
-
Рассмотрите теоретический материал по теме и примеры решения задач (приведены ниже).
-
Решите самостоятельную работу. Оформите решение письменно в тетради.
Ход работы.
-
Теоретический материал.
Расширение дроби. Значение дроби не меняется, если умножить её числитель и знаменатель на одно и то же число, отличное от нуля. Это преобразование называется расширением дроби. Например,
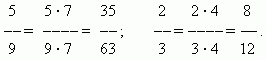
Сокращение дроби. Значение дроби не меняется, если разделить её числитель и знаменатель на одно и то же число, отличное от нуля. Это преобразование называется сокращением дроби. Например,
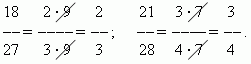
Сравнение дробей. Из двух дробей с одинаковыми знаменателями та больше, числитель которой больше:
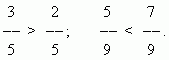
Для сравнения дробей, у которых знаменатели различны, необходимо расширить их, чтобы привести к общему знаменателю.
П р и м е р . Сравнить две дроби:
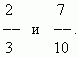
Решение
|
|
|
| |||||||||||||||||||||||||||||||||
|
Сложение и вычитание дробей. Если знаменатели дробей одинаковы, то для того, чтобы сложить дроби, надо сложить их числители, а для того, чтобы вычесть дроби, надо вычесть их числители (в том же порядке). Полученная сумма или разность будет числителем результата; знаменатель останется тем же. Если знаменатели дробей различны, необходимо сначала привести дроби к общему знаменателю. При сложении смешанных чисел их целые и дробные части складываются отдельно. При вычитании смешанных чисел мы рекомендуем сначала преобразовать их к виду неправильных дробей, затем вычесть из одной другую, а после этого вновь привести результат, если требуется, к виду смешанного числа. Пример . Умножение дробей. Умножить некоторое число на дробь означает умножить его на числитель и разделить произведение на знаменатель. Следовательно, мы имеем общее правило умножения дробей: для перемножения дробей необходимо перемножить отдельно их числители и знаменатели и разделить первое произведение на второе. П р и м е р. Деление дробей. Для того, чтобы разделить некоторое число на дробь, необходимо умножить это число на обратную дробь. Это правило вытекает из определения деления Пример Чтобы найти сумму или разность двух чисел, записанных в десятичной форме, надо выполнить три шага:
Пример. Найдите значение выражений: а) 8,125 + 17,4; б) 3,5 + 121,048. Решение а) б)
Если в одном из слагаемых нет десятичной точки, ее ставят справа от всего числа. Например, возьмем числа 5,83 и 72. В этом случае операция сложения будет выглядеть так:
| | ||||||||||||||||||||||||||||||||||
| №6. Найти сумму |
|
| 1 1
|
| № 7. Выполнить вычитание: |
|
| 1 1
|
| №8. вычислите. | 1) 0,28 · 12,5 + 3,51 : 3,9; 2) 0,0108 · 1600,5 - 1,47 : 2,1;
| 1) 6,3 · 1,08 - 6,4 : 25,6; 2) 132,5 · 0,0034 + 0,0425: 2,5;
| 3 3 |
| № 9. Вычислите |
|
| 4 |
| Критерии оценки | |
| Количество набранных баллов | оценка |
| 21 - 28 | 3 |
| 29 - 36 | 4 |
| 37 - 41 | 5 |
Практическая работа №4.
Вычисление параметров профессиональных величин.
Цели: закрепить умения и навыки выполнения действий с обыкновенными и десятичными дробями, правила округления при решении практических задач.
Оборудование: тетрадь для практических работ, ручка, методические рекомендации по выполнению работы
Указание. Практическая работа состоит из двух частей – теоретической и практической. После изучения теоретического материала можно приступать к выполнению практической части. Она состоит из одной или более задач для самостоятельного выполнения. Не забывайте о правильном оформлении решения
Порядок выполнения работы.
-
Рассмотрите теоретический материал по теме и примеры решения задач (приведены ниже).
-
Решите самостоятельную работу. Оформите решение письменно в тетради.
Теоретический материал. ( Смотреть практические работы №1-3)
Примеры решения задач:
Пример 1.
Задачи на составление уравнений Два водителя израсходовали 234 л горючего. Первый израсходовал в час на 0.5 л. меньше, чем второй, а работал на 1.5 часа больше. Сколько горючего в час израсходовал каждый водитель, если они израсходовали горючего поровну
Пример 2.
Есть два кулька и 100 гаек. Нужно распределить гайки по кулькам так, чтобы в одном кульке оказалось гаек в два раза больше чем во втором. Гайки пилить нельзя, распределены должны оказаться все гайки.
Решение Насыпаем в первый кулек 50 гаек. Затем в этот кулек вставляем второй и насыпаем еще 50 гаек. В итоге в первом кульке - 100, во втором –
Практическая работа №4.
Вычисление параметров профессиональных величин.
Цели: закрепить умения и навыки выполнения действий с обыкновенными и десятичными дробями, правила округления при решении практических задач.
Оборудование: тетрадь для практических работ, ручка, методические рекомендации по выполнению работы
Указание. Практическая работа состоит из двух частей – теоретической и практической. После изучения теоретического материала можно приступать к выполнению практической части. Она состоит из одной или более задач для самостоятельного выполнения. Не забывайте о правильном оформлении решения
Порядок выполнения работы.
-
Рассмотрите теоретический материал по теме и примеры решения задач (приведены ниже).
-
Решите самостоятельную работу. Оформите решение письменно в тетради.
Теоретический материал. ( Смотреть практические работы №1-3)
Примеры решения задач:
Пример 1. На сковороде помещается два кусочка хлеба. На поджаривание кусочка с одной стороны требуется одна минута. Как поджарить за три минуты три кусочка хлеба с обеих сторон ?
Решение
Сначала жаришь 2 кусочка с одной стороны, один кусочек переворачиваешь, другой откладываешь... вместо него кладешь новый кусочек, это уже 2 минуты. Значит 1 кусочек уже поджарен с 2-х сторон и 2 кусочка только с одной: вот и кладешь их на сковородку- 3 минуты.
Пример 2. В книге рецептов написано, что на три порции фруктового салата необходимо взять 150гр киви, 210гр манго,180гр папайи и 60гр миндальных орехов. По сколько грамм каждого ингредиента нужно для приготовления 20 порций фруктового салата.
Решение:
Выясним по сколько грамм каждого ингредиента нужно для приготовления одного салата.
1.Для этого каждый ингредиент разделим на три:
150/3=50гр киви.
210/3=70гр манго.
180/3=60гр папайи.
60/3=20гр миндальных орехов.
2. Умножим получившиеся результаты на 20порций.
50*20=1000гр киви.
70*20=1400гр манго.
60*20=1200гр папайи.
20*20=400гр миндальных орехов.
Ответ: на 20 порций фруктового салата необходимо :
1000гр киви,
1400гр манго,
1200гр папай
100гр миндальных орехов.
Механическая обработка овощей и грибов
Примеры решения задач.
-
Для приготовления блюда «Картофельное пюре» в столовой II категории 17 марта выделено 300 кг неочищенного картофеля. Определите какое количество очищенного картофеля получится при очистке?
Дано: Решение:
mбр = 300 кг m н = mбр х (100% - Нотх)
Нот = 40% 100%
mн =300 кг х (100% - 40%)=300кг х 60%= 180 кг
m н =? 100% 100%
Ответ: m н = 180 кг.
2. Масса жареного картофеля составляет 38 кг 640 г. Определите процент потерь при тепловой обработке, процент отходов при механической обработке и массу неочищенного картофеля в декабре месяце.
Дано: Решение:
При решении задачи воспользуемся таблицей №24
стр. 558 - (№32 стр. 651)1 «Расчет расхода сырья,
m г пр = 38,64 кг. выхода полуфабрикатов и готовых изделий.
Н пот - ? Н поп = 31%
Н отх - ? Н отх = 30%
m бр - ?
m н = m г пр х 100% = 38,64 х 100% = 56 кг
100% - Н пот 100% - 31%
m бр = m Н х 100% = 56 кг х 100% = 80 кг
100% - Н отх 100% - 30%
Ответ: 1) потери при тепловой обработке 31%
2) отходы при механической обработке 30%
3) масса брутто составляет 80 кг.
3. Масса неочищенного репчатого лука 50 кг, масса после очистки 43 кг.
Найдите процент отходов и сравните с нормой отходов по таблице №24 (36).
Дано: Решение:
m бр = 50 кг К отх = (mотх - mН) х 100% =
m Н = 43 кг m бр
К отх - ? = (50 кг - 43 кг) х 100% = 15%
50 кг
Н отк =16%
Ответ: Процент отходов лука меньше нормативного на 1%.
4. Масса очищенной моркови 35 кг.
Найдите массу неочищенной моркови на 16 ноября.
Дано: Решение:
m Н = 35 кг Норма отходов определена по таблице №24 на
Н отх =20% стр. 558 (№36 стр. 651) Сборника рецептур.
m бр - ? m бр = mН х 100% = 35 кг х 100% = 43,2 кг
100% - Н отх 80%
Ответ: Масса брутто моркови 43,2 кг.
Задачи для самостоятельного решения
1. Взято для очистки 110 кг картофеля в феврале месяце. Определите какова масса от -
ходов, если норма отходов 35%.
2. Масса очищенного картофеля 18 кг. Сколько было израсходовано неочищенного картофеля в ноябре месяце, если норма отходов составляет 30%.
3. Масса неочищенной моркови 50 кг. Определите, какова масса отварной моркови в феврале месяце, если норма отходов при механической обработке 25%, а потери при тепловой обработке 0,5%.
4. Для приготовления блюда «Перец фаршированный» было взято 8 кг перца сладкого. После механической обработки было получено 6 кг 360 г. перцев. Определите процент отходов и сравните с нормой отходов при механической обработке.
5. Масса очищенного картофеля 56 кг. Определите массу очищенного картофеля в мае месяце.
6. На производство поступило 200 кг неочищенного картофеля. Определите, сколько будет получено очищенного картофеля и картофеля жаренного брусочками во фритюре 15 декабря.
7. Для приготовления салата из свежих огурцов взято 4 кг свежих грунтовых огурцов неочищенных. Определите, какое количество огурцов будет получено после мойки, удаления плодоножки, верхушки, пятен от ожогов и порционировании.
8. Масса очищенного лука 17 кг 320 г. Какое количество лука пассированного до готовности будет получено.
9. Взято для очистки 80 кг картофеля. Определите процент отходов при механической обработке, если их масса 24 кг.
10. Масса отварного картофеля 12 кг. Найдите массу брутто на 5 ноября.
11. В столовой II категории 21 мая было очищено 60 кг. картофеля получиться при этом. Сколько порций отварного картофеля получится из этого картофеля.
12. В столовой III категории 3 января взято для очистки 25 кг моркови. Какое количество очищенной моркови получится. Сколько порций котлет морковных получится из этого количества.
Механическая обработка рыбы. Примеры решения задач
1. В столовую поступило 50 кг ставриды океанской специальной разделки. Определите какое количество филе с костей без костей получится при разделке.
Дано: Решение:
m бр = 50 кг При решении задачи воспользуемся таблицей №21 (27).
m филе - ? Рыба специальной разделки соответствует рыбе
непластованной (т.е. без чешуи, головы, плавников, внутренностей).Отходы при разделке непластованной рыбы установлены 39%, а при разделке на филе с кожей без костей - 54%.
Дополнительные отходы составляют 54% - 39% = 15%.
Выход рыбы непластованной 100% - 39% = 61%.
т.е. при поступлении рыбы спецразделки дополнительные отходы при разделке на филе составят:
61 - 100%
15-х х = 15 х 100 = 23,4%
61
таким образом, масса филе
50 кг - 100%
х 2 - 23,4% х 2 = 50 х 23,4 = 11,7 кг
100
m филе = 50 - 11,7 = 38,3 кг
Ответ: масса филе с кожей без костей составляет 38,3 кг.
Задачи для самостоятельного решения
1. Найдите процент отходов и потерь при холодной обработке для
а) Горбуши средней мороженой непластованной кусками.
б) Горбуши потрошенной с головой мороженой при разделке на филе без кожи и костей.
в) Камбалы дальневосточной неразделанной мороженой при разделке на кругляши.
г) Карась океанический потрошенный обезглавленный мороженный при разделке на филе с кожей без костей.
д) Мойва (мелочь III группы неразделанная) целая с головы.
е) Мойва (мелочь III группы неразделанная) целая с головой мороженная в брикетах.
2. На предприятие поступило 70 кг брутто сельди неразделанной. Определите, какое количество нетто сельди получится при обработке для жарки основным способом.
3. На предприятие поступило 82 кг скумбрии океанической неразделанной. Какое количество филе с кожей и реберными костями будет получено при разделке?
4. Какое количество филе с кожей без костей будет получено из 50 кг ставриды океанической неразделанной.
5. Найдите массу брутто морского окуня для приготовления 100 порций жареной рыбы (выход 75 г.), если поступил окунь морской потрошенный обезглавленный.
6. Найдите массу брутто терпуга для приготовления 100 порций жареной рыбы (выход 125 г.), если поступил терпуг неразделанный.
7. Определить размер отходов в % при обработке судака непластованного на филе без кожи и костей.
8. Определить размер отходов в % при обработке трески непластованной на филе с кожей без костей.
9. Какое количество филе без кожи и костей будет получено из 70 кг трески специальной разделки.
10. Какое количество филе форели с кожей без костей будет получено из 50 кг форели непластованной среднего размера.
Механическая обработка мяса, субпродуктов, птицы и дичи
Примеры решения задач.
1. Какое количество порций шницеля натурального рубленого с выходом 100 г. можно получить из полутуши говядины I категории массой 70 кг.
Дано: Решение:
m бр = 70 кг 1. По рецептуре №413, стр. 253 (657, стр. 313) масса
m гпр = 100 г. мяса для приготовления шницеля составляет 129 г.
(брутто).
n - ?
2. Из таблицы (12, стр. 502) «Нормы выхода крупнокусковых полуфабрикатов и котлетного мяса для предприятий общественного питания работающих на сырье» находим, что котлетное мясо составляет 40,3% от массы полутуши.
70 кг - 100%
х кг - 40,3% х = 70 кг х 40,3% = 28,21 кг100%
3.n = 28,21 кг: 0,129 кг = 218,6 шт. 218 шт.
Ответ: n = 218 шт.
Задачи для самостоятельного решения1. Найдите количество отходов по среднетушевым нормам отходов при поступлении 80 кг говядины II категории упитанности.
2. Найдите выход толстого и тонкого края говядины при поступлении 125 кг говядины I категории.
3. Сколько порций поджарки по рецептуре №376 (599) можно приготовить по колонке №2 из полутуши свинины жирной массой 60 кг.
4. Сколько порций блюда «Бефстроганов» по рецептуре №375 (598) можно приготовить по второй колонке из полутуши говядины II категории массой 75 кг.
5. Сколько порций блюда «Гуляш» по рецептуре №401 (632) можно приготовить из туши баранины I категории упитанности массой 46 кг по первой колонке.
6. При разделке свинины мясной выход мякоти составляет 86%, отходы 13,5% потери при разделке 0,5%. Определите массу мякоти, отходов и потерь, если масса туши 120 кг.
7. Масса разделанной говядины II категории упитанности 140 кг. Сколько говядины массой брутто было израсходовано.
8. Масса говяжьих охлажденных почек (брутто) 7 кг. Норма отходов при механической обработке 7%, потери при варке 47%. Определите массу отварных почек.
9. Масса говяжьей печени мороженой 17 кг. Определите массу жареной печени.
10. Масса говяжьей туши I категории упитанности составляет 110 кг. Определите массу мяса для жарки, тушения и варки крупными кусками.
11. Взято 35 кг. почек говяжьих охлажденных. После механической обработки получено 32 кг 620 г., а после варки 17 кг 615 г. почек. Определите фактический процент отходов при механической обработке, фактический процент потерь при тепловой обработке и сравните их с нормой. Если норма отходов 7%, а потерь 47%.
Супы
Пример решения задачи.
Найдите количество картофеля (брутто) для приготовления 30 порций борща украинского по рецептуре №116 (189) в апреле. Заменить томатное пюре на томатную пасту с содержанием сухих веществ 35-40%.
1. Масса порции борща составляет 500 г.
Таким образом, следует приготовить:
30 х 500 г. = 15000 г. = 15 кг борща
2. По рецепту №116 (189) масса нетто картофеля равна 160 г. на 1000 г. выхода.
Таким образом, m Н = 0,160 кг х 15 кг = 1,4 кг
Норма отходов картофеля в апреле состевляет 40% по таблице №24 (32)
m БР = 1,4 кг х 100% = 2,3 кг
100% - 40%
3. При приготовлении борща на 1000 г. выхода берут 30 г. томатного пюре, т.е.
0,030 х 15 = 0,45 кг
Замену на томатную пасту произведем с помощью таблицы №26 (36) «Нормы взаимозаменяемости продуктов при приготовлении блюд», где Â = 0,3, по формуле:
х = а х с х Â, где
х - масса заменяющего продукта
а - масса заменяемого продуктов на 1 порцию
с - количество порций
 - коэффициент взаимозаменяемости или эквивалентная масса продуктов брутто.
х = 0,45 х 0,3 = 0,135 кг
Ответ: для 30 порций борща украинского в апреле необходимо взять 2,3 кг неочищенного картофеля и 0,135 кг томатной пасты.
Задачи для самостоятельного решения
-
Рассчитайте количество продуктов необходимое для приготовления и подачи 60 порций борща по рецептуре №109 (175), если масса порции составляет 400 г.
-
Определите норму расхода сырья для приготовления и подачи 50 порций блюда «Щи из свежей капусты с картофелем» по рецептуре №120 (119) в столовой 3 категории, если масса порции 350 г. Замените пюре томатное на сок томатный натуральный.
-
Определите норму расхода сырья для приготовления 100 порций мясных фрикаделек для супа «Суп картофельный с мясными фрикадельками» №135 (224) в столовой 2-й категории.
-
Определите расход сырья для приготовления 50 порций блюда «Рассольник ленинградский» №129 (213) в столовой 3 категории на 15 января.
-
Определите расход сырья для приготовления 80 порций блюда «Суп картофельный» №131 (215) в столовой II категории на 2 февряля.
-
Определите норму расхода сырья для приготовления 30 порций супа молочного с овощами №163 (261) в столовой II категории. Замените молоко цельное натуральное на молоко коровье цельное сухое.
Соусы
-
Рассчитать количество соуса красного основного для отпуска 60 порций блюда «Язык отварной с соусом» в столовой II категории по рецептуре №358 (570). И рассчитать количество продуктов для приготовления этого соуса.
-
Рассчитать необходимое количество продуктов для приготовления соуса лукового по рецептуре №530 (827) в столовой 3 категории в количестве 5,5 кг (включая продукты для приготовления соуса красного основного рецептуры №528 (824).
-
Рассчитайте необходимое количество продуктов для приготовления 3 кг соуса молочного сладкого по рецептуре №550 (860) по II колонке. Замените молоко цельное на молоко коровье обезжиренное сухое.
-
Рассчитайте необходимое количество продуктов для приготовления 5 кг соуса белого основного в столовой 3 категории по рецептуре №537 (843), включая продукты для приготовления бульона. Замените лук репчатый на лук репчатый сушеный.
Каши и блюда из них Блюда из макаронных изделий
Примеры решения задач.
-
Рассчитайте необходимое количество продуктов для приготовления 30 порций каши рисовой молочной в столовой 2-й категории. Котел какого объема нужно взять для этого.
1) Для решения задачи воспользуемся рецептурой №257 (411) «Каша вязкая», из которой видно, что масса каши 200 г.
200 х 30 = 6000 г. = 6 кг
2) При расчете количества продуктов воспользуемся таблицей №4 стр. 149 (8) «Количество крупы, жидкости, соли, расходуемое на приготовление каш».
а) рис: берется в количестве 222 г. на 1 кг каши, таким образом
0,222 х 6 = 1,330 г.
б) жидкость: расходуется в количестве 0,82 л на 1 кг каши, причем 60% составляет молоко (смотрите примечание к таблице).
0,82 х 6 = 4,92 л. жидкости
4,92 л - 100%
х1л - 60% х1 = 4,92 х 60% = 2,952 л.молока
100%
4,92 - 2,95 = 1,97 л. воды
в) при расчете необходимого количества сахара воспользуемся примечанием к таблице №4 (8)
сахара добавляют из расчета 30 г. на 1 кг готовой каши
0,030 х 6 = 0,18 кг
г) соль добавляют из расчета 4 - 5 г на 1 кг каши.
0,004 х 6 = 0,024 кг
0,005 х 6 = 0,030 кг
3) При расчете объема котла необходимо помнить, что готовая каша должна занимать не более 80% объема котла.
6 кг - 80%
х2 кг - 100% х2 = 6 кг х 100% = 7,5 л » 10 л
80%
Ответ: Для приготовления 30 порций каши необходимо взять:
1) Рис. - 1,33 кг
Молоко - 2,95 л
Воды - 1,97 л
Сахара - 0,18 кг
Соли - 0,024 - 0,030 кг
2) Для варки каши берем котел объемом 10 л.
-
Найдите необходимое количество жидкости и соли для варки рассыпчатой рисовой каши из 8 кг риса промытого.
-
Для решения задачи воспользуемся таблицей №4 стр. 149 (8) на стр. (179)
Объем 1 кг крупы с водой по таблице равен
2,1 + 1 = 3,1 л
т. к. при промывании в крупе остается примерно 10% воды от массы сухой крупы, т.е. в данном случае 100 г., то
3,1 - 0,1 = 3 л
-
Объем 8 кг крупы с водой
3 х 8 = 24 л
-
Количество воды, которая наливается в котел
24 - 8 = 16 л
-
Соль рассчитываем исходя из таблицы, количество соли на 1 кг
крупы - 28 г.
28 г. х 8 = 224 г.
Задачи для самостоятельного решения
-
Рассчитайте необходимое количество продуктов для приготовления 150 порций каши рассыпчатой гречневой с луком по рецептуре 256 (406) в столовой 3 категории.
-
Рассчитайте необходимое количество жидкости и соли для варки рассыпчатой ячневой каши из 4 кг крупы, а также объем котла, необходимый для варки каши.
-
Рассчитайте необходимое количество продуктов для приготовления запеканки рисовой с творогом по рецептуре №265 (420) в количестве 120 порций, в столовой II категории.
-
Какое количество порций крупеника можно получить из 5 кг гречневой крупы в столовой II категории.
-
Рассчитайте количество продуктов необходимое для приготовления 50 порций блюда «Макароны с томатом» по рецептуре 275 (445) в столовой 3 категории.
-
Рассчитайте количество продуктов необходимое для приготовления 20 порций блюда «Лапшевик с творогом» по рецептуре 278 (452) в столовой 3 категории.
-
Определите норму расхода крупы, молока, воды, соли и сахара для варки
50 кг пшенной вязкой каши по II колонке.
-
Определите норму расхода продуктов для варки жидкой каши из хлопьев «Геркулес» из 2 кг крупы по III колонке.
-
Определите норму расхода продуктов для варки рассыпчатой пшеничной каши и 4 кг пшеничной крупы по II колонке.
10.Рассчитайте количество жидкости и соли для варки рассыпчатой перловой каши из 5 кг крупы перловой промытой.
11.Рассчитайте количество жидкости и соли для варки рассыпчатой кукурузной каши из 10 кг крупы кукурузной промытой.
Блюда и гарниры из овощей
Задачи для самостоятельного решения
-
Масса отварного картофеля 25 кг. Определите процент потерь при тепловой обработке, процент отходов при механической обработке и массу неочищенного картофеля в апреле месяце.
-
Взято для очистки 100 кг картофеля в ноябре месяце. Определите массу картофеля жареного брусочками фри.
-
Масса отварной моркови 15 кг. Определите массу неочищенной моркови в ноябре, марте месяце.
-
Какое количество отварного картофеля получиться в апреле месяце из 80 кг неочищенного картофеля.
-
Какое количество моркови припущенной дольками получиться в феврале месяце из 15 кг сырой неочищенной моркови.
-
Какое количество картофеля жареного во фритюре брусочками получиться в марте месяце из 10 кг неочищенного картофеля.
-
Рассчитайте необходимое количество продуктов для приготовления 50 порций блюда «Капуста тушеная» в столовой III категории.
-
Рассчитайте необходимое количество продуктов для приготовления 20 порций блюда «Картофеля в молоке» в мае месяце в столовой 2 категории.
-
Рассчитайте необходимое количество продуктов необходимое для приготовления 25 порций блюда «Картофель запеченный в сметанном соусе» по рецептуре №270 (372) в столовой III категории. Замените картофель свежий пюре картофельным сухим.
Блюда из рыбы
-
Какое количество порций окуня отварного (филе) можно получить из 4 кг окуня морского потрошеного обезглавленного, в столовой II категории.
-
Рассчитайте количество продуктов необходимое для приготовления 12 порций блюда «Рыба припущенная с соусом белое вино» по рецептуре №306 (509) в столовой II категории, если на предприятие поступил судак.
-
Какое количество порций ставриды жареной можно получить из 7 кг ставриды океанической в столовой 3 категории.
-
Рассчитайте количество продуктов необходимое для приготовления 30 порций блюда «Рыба жареная во фритюре» по рецептуре №313 (525) в столовой II категории.
-
Рассчитайте количество продуктов необходимое для приготовления 75 порций блюда «Котлеты рыбные» по рецептуре №324 (541) из трески в столовой III категории.
-
На предприятие поступило 50 кг Горбуши не разделанной. После разделки на кругляши осталось 34,5 кг рыбы. После варки масса рыбы составила 27,6 кг. Определите отходы при механической обработке и потери при тепловой обработке и сравните с нормативными показателями из таблицы №21 (27).
Блюда из мяса и мясных продуктов
-
Масса говядины для варки 20 кг. После варки масса мяса составила 12,9 кг. Найдите потери при тепловой обработке и сравните с нормой.
-
Сколько порций ростбифа можно получить из 1,8 кг вырезки в ресторане I категории.
-
Рассчитайте количество продуктов необходимое для приготовления 75 порций блюда «Бефстроганов» в столовой II категории.
-
В столовой обнаружено 6,5 кг говядины тушеной крупным куском. Какое количество мяса было взято для этого.
-
Рассчитайте количество продуктов необходимое для приготовления 50 порций блюда «Гуляш» в столовой III категории из говядины II категории упитанности.
-
Какое количество котлет натуральных рубленных будет получено из туши баранины массой 47 кг в столовой II категории.
-
Какова масса отваренной курицы, если масса заправленной тушки 1,8 кг. Определите количество отходов при порционировании.
-
Рассчитайте необходимое количество продуктов (включая воду) для приготовления 50 порций плова из свинины в столовой III категории.
Блюда из яиц и творога
Пример решения задач
-
Рассчитай массу готовой яичницы в столовой II категории из яиц массой 49 г.
Дано: Решение:
m бр = 49 г. Исходя из рецептуры №281 (459) «Яичница глазунья натуральная» для приготовления блюда используют 3 яйца и 10 г. сливочного масла.
Выход яичницы определяем по формуле:
m Н = m яиц в скорлупе х , для яиц массой больше 46 г. равен 0,88.
m Н = 49 х 3 х 0,88 = 147 г.
m гот = (mН + жир) х 88 = (147 + 10) х 88 = 138 г
100 100
Ответ: выход яичницы 138 г.
Задачи для самостоятельного решения
-
Рассчитайте выход готовой яичницы в столовой III категории из яиц масой 44 г.
-
Рассчитайте массу готового омлета в столовой II из яиц массой 48 г.
-
Замените яйца на яичный порошок при приготовлении 50 порций омлета с сыром по рецептуре №285 (471) в столовой II категории.
-
Рассчитайте количество продуктов необходимое для приготовления 70 порций блюда «Вареники ленивые» в столовой II категории.
-
Рассчитайте количество продуктов необходимое для приготовления 80 порций блюда «Сырники из творога» в столовой III категории. И замените творог жирный на творог полужирный.
Холодные блюда и закуски
-
Рассчитайте количество продуктов необходимое для приготовления 50 бутербродов с маслом по рецептуре № (1)1 с селедочным маслом по рецептуре № (879).
-
Рассчитайте количество продуктов необходимое для приготовления 50 порций салата «Весна» по рецептуре №23 (62) в столовой II категории, если масса порции 100 г.
-
Рассчитайте количество продуктов необходимое для приготовления 70 порций винегрета овощного по рецептуре №60 (103) в столовой II категории, если масса порции 150 г., на 10 декабря.
-
Рассчитайте количество продуктов необходимое для приготовления 75 порций блюда «Рыба жареная под маринадом» по рецептуре №87 (146) в столовой II категории, включая продукты для маринада, из окуня морского.
Сладкие блюда и напитки
-
Определите норму расхода продуктов для изготовления 300 порций компота из яблок и слив по рецептуре №586 (926/III - 81 г.). Если масса порции 200 г.
-
Определите норму расхода продуктов для изготовления 400 порций компота из сухофруктов по рецептуре №588 (933) в столовой II категории. Если, масса порции 200 г. Замените сахара - песок на мед натуральный.
-
Определите норму расхода продуктов для изготовления 150 порций киселя из клюквы по рецептуре №590 (934) в столовой II категории если масса порции 200 г. Замените крахмал картофельный сухой на крахмал картофельный сырец (50%-й влажности).
-
Определите норму расхода продуктов для изготовления 80 порций желе из молока по рецептуре №605 (962). В столовой III категории, если масса порции 150 г. Замените молоко цельное на молоко сгущенное стерилизованное в банках.
-
Определите норму расхода сырья для приготовления 50 порций блюда «Пудинг сухарный» по рецептуре №616 (983) в столовой II категории.
-
Определите норму расхода чая сухого для приготовления 200 порций чая с сахаром по рецептуре №628 (1009).
-
Определите норму расхода чая сухого для приготовления 300 порций чая с молоком по рецептуре №630 (1011).
Приложение
Основные формулы, используемые при решении задач.
m Н = mбр х (100% - Нотх)
m бр = mН х 100%
100% - Н отх
К отх = (mбр - mН) х 100%
m бр, где
m Н - масса нетто, г
m бр - масса брутто, г
Н отх - отходы при механической обработке, в процентах к массе сырья
брутто (определяем по таблицам сборника рецептур)%.
К отх - отходы при механической обработке продуктов, в процентах к
массе сырья брутто, %.
m гпр = mН х (100% - Нпот)100%
m Н = mгпр х 100%
100% - Н пот
К пот = (mН - mгпр) х 100%
m Н, где
m гпр - масса готового продукта, г.
m Н - масса нетто, г.
Н пот - потери при тепловой обработке сырья, в% к массе нетто
продукта (определяем по сборнику рецептур), %.
К пот - фактические потери при тепловой обработке продуктов в
процентах к массе нетто, %.
Практические задания к письменной экзаменационной работе по предмету «Кулинария»
-
Рассчитайте количество продуктов необходимое для приготовления 75 порций блюда «Винегрет овощной» /№103/ массой 100 г. на 15 января в столовой II категории.
-
Рассчитайте количество продуктов необходимое для приготовления 60 порций блюда «Винегрет овощной» /№103/ массой 100 г. на 2 февраля в столовой III категории. Замените огурцы соленые на огурцы консервированные маринованные.
-
Рассчитайте количество продуктов необходимое для приготовления 50 порций блюда «Борщ» /№175/ в столовой II категории на 11 ноября. Замените томатное пюре на томатную пасту с содержанием сухих веществ 25-30%.
-
Рассчитайте количество продуктов необходимое для приготовления 60 порций блюда «Борщ с капустой и картофелем» /№176/ в столовой II категории на 5 ноября.
-
Рассчитайте количество продуктов необходимое для приготовления 140 порций блюда «Борщ сибирский» /№183/ с толовой II категории на 5 ноября.
-
Рассчитайте количество продуктов необходимое для приготовления 80 порций блюда «Борщ украинский» /№189/ в столовой II категории на 1 ноября.
-
Рассчитайте количество продуктов необходимое для приготовления 50 порций блюда «Щи из свежей капусты с картофелем» /№197/ в столовой II категории на 30 января. Замените свежую морковь на сушенную.
-
Рассчитайте количество продуктов необходимое для приготовления 60 порций блюда «Щи из свежей капусты с картофелем» /№197/ в столовой II категории на 3 ноября. Замените томатное пюре с содержанием сухих веществ
12% на томатную пасту с содержанием сухих веществ 25-30%.
-
Рассчитайте количество продуктов необходимое для приготовления 20 порций блюда «Щи суточные» /№202/ в столовой II категории на 3 ноября. Замените томатное пюре с содержанием сухих веществ 12% на томатную пасту с содержанием сухих веществ 25-30%.
10.Рассчитайте количество продуктов необходимое для приготовления 30 порций блюда «Суп с крупой и мясными фрикадельками» /№241/ в столовой III категории на 3 января. Замените морковь свежую столовую на сушенную.
11.Рассчитайте количество продуктов необходимое для приготовления 300 порций блюда «Картофельное пюре» /№326/ в столовой II категории на 2 февраля. Замените молоко коровье пастеризованное цельное на молоко коровье цельное сухое.
12.Рассчитайте количество продуктов необходимое для приготовления 140 порций блюда «Картофельное пюре» /№326/ в столовой III категории на 3 февраля. Замените картофель свежий на пюре картофельное сухое.
13.Рассчитайте количество продуктов необходимое для приготовления 25 порций блюда «Кабачки фаршированные» /№402/ в столовой III категории на 3 февраля.
14.Рассчитайте количество продуктов необходимое для приготовления 50 порций блюда «Каша рисовая вязкая» /№411/ в столовой II категории. Замените молоко коровье цельное на молоко цельное сухое.
15.Рассчитайте количество продуктов необходимое для приготовления 150 порций блюда «Каша овсяная жидкая» /№411/ в столовой II категории. Определите емкость котла, необходимого для варки каши.
16.Рассчитайте количество продуктов необходимое для приготовления 200 порций блюда «Каша ячневая вязкая» /№411/ в столовой II категории. Замените коровье молоко цельное на молоко цельное сухое.
17.Рассчитайте количество продуктов необходимое для приготовления 200 порций блюда «Каша пшеничная рассыпчатая» /№405/ в столовой III категории. Определите емкость котла необходимого для варки каши.
18.Рассчитайте количество продуктов необходимое для приготовления 80 порций блюда «Каша манная жидкая» /№417/ в столовой II категории. Замените молоко коровье цельное на сливки сухие.
19.Рассчитайте количество продуктов необходимое для приготовления 110 порций блюда «Каша перловая рассыпчатая» /№405/ в столовой II категории. Определите емкость котла необходимого для каши.
20.Рассчитайте количество продуктов необходимое для приготовления блюда «Рагу из овощей /№348/ в количестве 180 порций, в столовой II категории на 12 ноября.
21.Рассчитайте количество продуктов необходимое для приготовления блюда «Соус красный основной» /№824/ в количестве 250 порций массой 75 г. в столовой III категории. Замените лук репчатый свежий на лук репчатый сушенный.
22.Рассчитайте количество продуктов необходимое для приготовления блюда «Соус луковый» /№827/ в количестве 200 порций массой 50 г., в столовой III категории. Замените томатное пюре на томатную пасту с содержанием сухих веществ 35-40%.
23.Рассчитайте количество продуктов необходимое для приготовления блюда «Соус красный с луком и огурцами» /№828/ в количестве 80 порций массой 75 г. в столовой III категории. Замените лук репчатый свежий на лук репчатый сушенный.
24.Рассчитайте количество продуктов необходимое для приготовления 120 порций блюда «Котлеты картофельные» /№357/ в столовой II категории на 15 сентября. Замените картофель свежий продовольственный на пюре картофельное сухое.
25.Рассчитайте количество продуктов необходимое для приготовления 75 порций блюда «Картофельное пюре запеченое» /№376/ в столовой III категории на 3 ноября. Замените молоко коровье цельное на молоко коровье сухое цельное.
26.Рассчитайте количество продуктов необходимое для приготовления блюда «Соус белый с овощами» /№846/ в количестве 140 порций массой 75 г. в столовой II категории. Замените морковь свежую столовую на морковь сушеную.
27.Рассчитайте количество продуктов необходимое для приготовления блюда «Соус красный с вином» /№826/ в количестве 75 порций массой 50 г. в столовой II категории. Замените томатное пюре на томатную пасту с содержанием сухих веществ 25-30%.
28.Рассчитайте количество продуктов необходимое для приготовления 200 порций массой 75 г. блюда «Соус томатный» /№848/ в столовой III категории. Замените томатное пюре на томатную пасту с содержанием сухих веществ 25-30%.
29.Рассчитайте количество продуктов необходимое для приготовления 70 порций массой 50 г. блюда «Соус молочный сладкий» /№860/ в столовой II категории. Замените молоко натуральное коровье на молоко сгущенное стерилизованное в банках.
30.Рассчитайте количество продуктов необходимое для приготовления блюда «Маринад овощной с томатом» /№892/ в количестве 160 порций 75 г. в столовой II категории на 15 сентября. Замените морковь свежую на сушенную, а также, томатное пюре на томатную пасту с содержанием сухих веществ 25-30%.
31. Рассчитайте количество продуктов необходимое для приготовления 150 порций по 200 г. блюда «Кисель из плодов или ягод свежих» /№934/ в столовой II категории. Замените сахар-песок на мед натуральный, а также, крахмал картофельный сухой /20% влажности/ на крахмал картофельный сырец /50% влажности/.
32. Рассчитайте количество продуктов необходимое для приготовления 75 порций массой 200 г. блюда «Кисель молочный» /№952/ в столовой II категории. Замените сахар - песок на рафинадную пудру и молоко коровье цельное на молоко обезжиренной сухое.
33. Рассчитайте количество продуктов необходимое для приготовления 120 порций блюда «Капуста тушенная» /№342/ в столовой III категории на 5 апреля. Замените морковь свежую столовую на морковь сушенную.
34. Рассчитайте количество продуктов необходимое для приготовления 18 порций массой 150 г. блюда «Желе из молока» /№962/ в столовой II категории. Замените желатин на агароид.
35. Рассчитайте количество продуктов необходимое для приготовления 60 порций массой 100 г. блюда «Желе из молока» /№962/ в столовой II категории. Замените молоко коровье цельное на молоко цельное сгущенное с сахаром.
Практическая работа 3.
Решение практических задач.
Цели: научиться определять абсолютную и относительную погрешности числа; научиться определять верные значащие цифры числа; научиться определять погрешности функций
Оборудование: тетрадь для практических работ, ручка, методические рекомендации по выполнению работы
Указание. Практическая работа состоит из двух частей – теоретической и практической. После изучения теоретического материала можно приступать к выполнению практической части. Она состоит из одной или более задач для самостоятельного выполнения. Не забывайте о правильном оформлении решения
Порядок выполнения работы.
-
Рассмотрите теоретический материал по теме и примеры решения задач (приведены ниже).
-
Решите самостоятельную работу. Оформите решение письменно в тетради.
Ход работы.
Теоретический материал
Понятие погрешности числа
Разность точного и приближенного значений величины называется погрешностью приближения (обозначается 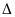 х),
х),
т.е. 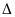 х=х-а - погрешность приближения
х=х-а - погрешность приближения
откуда х=а+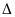 х,
х,
т.е. истинное значение равно сумме приближенного значения и погрешности приближения.
Модуль разности точного и приближенного значений величины называется абсолютной погрешностью приближенного значения числа х.
т.е. 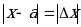 -абсолютная погрешность приближения.
-абсолютная погрешность приближения.
Запись х= а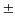 h означает, что истинное значение величины х заключено между границами, т.е. а - h
h означает, что истинное значение величины х заключено между границами, т.е. а - h 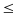 х
х 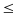 а + h
а + h
Пример 1. На предприятии 1284рабочих и служащих. При округлении этого числа до 1300 абсолютная погрешность составляет 1300 -1284 = 16. При округлении до 1280 абсолютная погрешность составляет 1284 - 1280 = 4.
Пример 2. Даны приближенные значения числа х=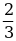 ;
; 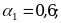
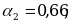
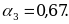 Какое из этих трех приближений является лучшим?
Какое из этих трех приближений является лучшим?
Решение:
Находим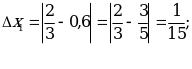
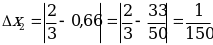 ;
; 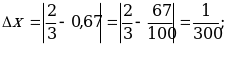 Лучшим приближением числа х является
Лучшим приближением числа х является 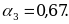
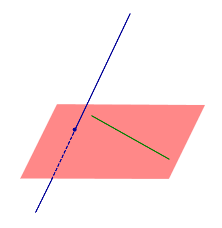
Пример 3. Длина детали х (см) заключена в границах 33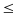 х
х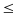 34. Найти границу абсолютной погрешности измерения детали.
34. Найти границу абсолютной погрешности измерения детали.
Решение: Примем за приближенное значение длины детали среднее арифметическое границ: а=(33+34)/2 = 33,5 (см).
Тогда граница абсолютной погрешности приближенного значения длины детали не превзойдет 0,5 (см). Величину 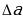 можно найти и как полуразность верхней и нижней границ, т.е.
можно найти и как полуразность верхней и нижней границ, т.е. 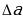 = (34-33)/2 = 0,5 (см). Длина детали х, найденная с точностью до
= (34-33)/2 = 0,5 (см). Длина детали х, найденная с точностью до 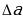 =0,5 (см), заключена между приближенными значениями числа х:
=0,5 (см), заключена между приближенными значениями числа х:
33,5-0,5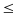 х
х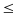 33,5+0,5;
33,5+0,5;
х=33,5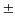 0,5 (см).
0,5 (см).
Отношение абсолютной погрешности приближения к модулю приближенного значения величины называется относительной погрешностью приближения и обозначается 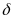 .
.
Т.е.
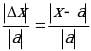 =
=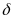 является относительной погрешностью приближения
является относительной погрешностью приближения
Пример 1. При измерении длины L и диаметра проводника получили L=(10,0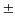 0,1) м, d = (2,5
0,1) м, d = (2,5 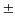 0,1) мм. Какое из этих измерений точнее?
0,1) мм. Какое из этих измерений точнее?
Решение: Измерение длины проводника производилось с точностью до 0,1м=100мм, а измерение диаметра проводника – с точностью до 0,1мм.
При измерении длины проводника допускается абсолютная погрешность в 100мм на 10000мм, и, следовательно, допустимая абсолютная погрешность составляет
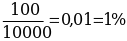 измеряемой величины.
измеряемой величины.
При измерении диаметра допустимая абсолютная погрешность составляет
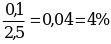 измеряемой величины. Следовательно, измерение длины проводника выполнено точнее.
измеряемой величины. Следовательно, измерение длины проводника выполнено точнее.
Пример 2. Известно, что 0,111 является приближенным значением для 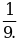 Найти абсолютную и относительную погрешности этого приближения.
Найти абсолютную и относительную погрешности этого приближения.
Решение: Здесь х=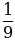 , а=0,111. Тогда
, а=0,111. Тогда 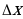 = х-а = 1/9 – 0,111 = 1/9000-а.п.п,
= х-а = 1/9 – 0,111 = 1/9000-а.п.п,
 -о.п.п
-о.п.п
Пример 3. В школе 197 учащихся. Округляем это число до 200. Абсолютная погрешность составляет 200-197 = 3. Относительная погрешность равна 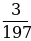 или, округленно,
или, округленно,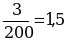 %.
%.
В большинстве случаев невозможно узнать точное значение приближенного числа, а значит, и точную величину погрешности. Однако почти всегда можно установить, что погрешность (абсолютная или относительная) не превосходит некоторого числа.
Пример 4.
Продавец взвешивает арбуз на чашечных весах. В наборе гирь наименьшая— 50 г. Взвешивание дало 3600 г. Это число — приближенное. Точная масса арбуза неизвестна. Но абсолютная погрешность не превышает 50 г. Относительная погрешность не превосходит 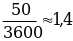 %.
%.
Самостоятельная работа.
| № | 1 вариант | 2 вариант | ||
| Найдите абсолютную погрешность округления до единиц следующих чисел: | ||||
| 1 | 1) 0,8; 2) 7,6; 1 балл 1 балл | 3) 19,3; 4) 563,58. 1 балл 1 балл | ||
| 2 | Граница абсолютной погрешности приближенного значения 386 числа х = 0,5. Укажите границы, в которых заключено число х. 2 балла | Найдите границу абсолютной погрешности измерений, полученных в виде неравенства 37 2 балла | ||
| 3 | Амперметр дает точность | Атомная масса водорода 1,0082 | ||
| 4 | Шоколадка стоит 40 рублей. В воскресенье в супермаркете действует специальное предложение: заплатив за две шоколадки, покупатель получает три (одну в подарок). Сколько шоколадок можно получить на 320 рублей в воскресенье? 2 балла | В университетскую библиотеку привезли новые учебники по геометрии для 2—3 курсов, по 280 штук для каждого курса. Все книги одинаковы по размеру. В книжном шкафу 7 полок, на каждой полке помещается 30 учебников. Сколько шкафов можно полностью заполнить новыми учебниками? 2 балла | ||
| 5 | Больному прописано лекарство, которое нужно пить по 0,5 г 3 раза в день в течение 21 дня. В одной упаковке 10 таблеток лекарства по 0,5 г. Какого наименьшего количества упаковок хватит на весь курс лечения? 2 балла | Больному прописано лекарство, которое нужно пить по 0,5 г 3 раза в день в течение 21 дня. В одной упаковке 10 таблеток лекарства по 0,5 г. Какого наименьшего количества упаковок хватит на весь курс лечения? 2 балла | ||
| 6 | Граница абсолютной погрешности приближенного значения a равна h. Найдите границы, в которых Заключено число x, если:
| |||
|
| a=23; h=0.5; 2 балла | a=1.5; h=0.01; 2 балла | ||
| Критерии оценки | |
| Количество набранных баллов | оценка |
| 6-8 | 3 |
| 9-10 | 4 |
| 11-14 | 5 |
|
|
|
Практическая работа 5.
Решение практических задач.
Цели: научиться определять абсолютную и относительную погрешности числа; научиться определять верные значащие цифры числа; научиться определять погрешности функций
Оборудование: тетрадь для практических работ, ручка, методические рекомендации по выполнению работы
Указание. Практическая работа состоит из двух частей – теоретической и практической. После изучения теоретического материала можно приступать к выполнению практической части. Она состоит из одной или более задач для самостоятельного выполнения. Не забывайте о правильном оформлении решения
Порядок выполнения работы.
-
Рассмотрите теоретический материал по теме и примеры решения задач (приведены ниже).
-
Решите самостоятельную работу. Оформите решение письменно в тетради.
Теоретический материал.
Пропорцией называют равенство отношений двух или нескольких пар чисел или величин. Например, размеры модели машины или сооружения отличаются от размеров оригинала одним и тем же множителем, задающим масштаб модели. При расчете количества продуктов на порцию блюда необходимо повторить умножение десятичной дроби на натуральное число
Чтобы умножить десятичную дробь на натуральное число, нужно перемножить числа, не обращая внимание на запятую, затем в результате отделить запятой столько знаков, сколько их в десятичной дроби.
Основное свойство пропорции: произведение крайних равно произведению средних, проверим это:
8,6 х 4 = 17,2 х 2
34,4 = 34,4
Решим пропорцию:
2,8: х = 5,6 : 4
Найдем х,
5,6 х х = 2,8 х 4
5,6 х = 11,2
х = 2
При расчете расхода продуктов для приготовления блюд нужно помнить что и уметь переводить граммы в
| 1 кг = 1000г 1г = 0.001 кг 10 г =0,01 кг 100 = 0,1 кг |
Например: 350 г = 0,350 кг
18 г = 0,018 кг
5 г = 0,005 кг
750 г = 0,75 кг
Примеры.
Задача 1. Для приготовления блюда выделено 300 кг неочищенного картофеля (масса брутто). Определить массу отходов при его первичной обработке, если норма отходов установлена в 40% от массы брутто.
Решение
Данное в задаче число 300 кг является начальным, так как в процентах от него дается норма отходов. Оно содержит 100% масса отходов искомое число. Оно содержит 40%.
Данное число 300кг содержит 100%.
Искомое число X кг 40%
Составляем пропорцию:
300: 100=Х:40
Х=300х40 =120кг
100
Ответ: масса отходов 120кг.
Задача 2. Для приготовления блюд нужно израсходовать 180 кг очищенного картофеля (масса нетто). Сколько неочищенного картофеля (масса брутто) следует взять, если отходы при холодной обработке составляют 40% от массы брутто.
Решение
Начальным числом является масса брутто. Это искомое число. Оно содержит 100%. Данное число 180кг содержит 100%-40%=60% (так как масса нетто равна массе брутто за вычетом массы отходов)
180кг содержит 60%
Х кг 100%
Составляем пропорцию:
180 : 60 = Х : 100
Х = 180х100 =300кг
60
Ответ: масса брутто равна 300 кг
Задача 3. Масса картофеля (брутто) 300кг. Масса отходов при его обработке 120кг. Определите процент отходов.
Решение
Начальное число 300 кг, следует найти процент отходов, т.е. массу 120 кг выразить в %
300 кг – 100%
120 кг – х %
Решим пропорцию х = 120 кг х 100% = 40%
300 кг
Ответ: масса отходов соответствует 40 %
2. Самостоятельная работа
I Вариант
1. Взято для очистки 80 кг картофеля определите, каким должна быть масса отходов, если норма отходов установлена 30 % от массы брутто.
2. Масса очищенного картофеля 56 кг (масса нетто). Сколько было израсходовано неочищенного картофеля, если норма отходов 30 %?
3. При разделке свинины мясной выход составляет 86% отходы 13,5 кг. Определите массу отходов.
II Вариант
1. Взято для очистки 80 кг картофеля. Определите процент отходов при холодной обработке, если их масса 24 кг.
2. Масса разделанной говядины
180 кг. Сколько было израсходовано говядины (массой брутто), если норма отходов составляет 26%
3. Определить массу отходов, если переработали 120 кг моркови, отходы составляют 30 %.
На примере одной технологической карты показать:
1. Рассчитать процент отхода каждого продукта
2. Рассчитать норму продуктов блюда на 120 порций (масса брутто)
3. Рассчитать цену 1 порции.
| Наименование сырья | Массовая доля сухих веществ % | Расход сырья на 100 шт. готовых изделий г. |
|
|
|
| в натуре | в сухих веществах |
| Мука пшеничная высшего сорта | 85,50 | 5592,0 | 4781,2 |
| Сахар песок | 99,85 | 1594,0 | 1591,6 |
| Масло сливочное | 84,00 | 1230,0 | 1033,2 |
| Меланж | 27,00 | 1118,0 | 301,9 |
| Дрожжи прессованные | 25,00 | 224,0 | 56,0 |
| Соль | 96,50 | 16,8 | 16,2 |
| Изюм | 80,00 | 559,0 | 447,2 |
| Цукаты | 83,00 | 280,0 | 232,4 |
| Ядра орехов сырые для обсыпки | 94,00 | 112,0 | 105,3 |
| Пудра ванильная | 99,85 | 37,7 | 37,6 |
| Пудра рафинадная | 99,85
| 112,0 | 11,8
|
Практическая работа № 7.
Логарифм.
Цели: научиться вычислять простые логарифмы
Оборудование: тетрадь для практических работ, ручка, методические рекомендации по выполнению работы
Указание. Практическая работа состоит из двух частей – теоретической и практической (задания для самостоятельного выполнения). После изучения теоретического материала можно приступать к выполнению практической части.
Порядок выполнения работы.
-
Рассмотрите теоретический материал по теме и примеры решения задач (приведены ниже).
-
Решите самостоятельную работу. Оформите решение письменно в тетради.
Ход работы.
-
Теоретический материал.
Логарифм положительного числа ![]() по основанию
по основанию ![]() (обозначается logab) — это показатель степени, в которую надо возвести
(обозначается logab) — это показатель степени, в которую надо возвести ![]() , чтобы получить
, чтобы получить ![]() (числа b, a – положительные, а≠ 1).
(числа b, a – положительные, а≠ 1).
Если aс = b, то logаb= с
![]()
 основное логарифмическое тождество
основное логарифмическое тождество
-
logа1 = 0
-
logаа = 1
-
logaax = x
частные случаи логарифма

-
П
Пример 5. Вычислите log6
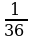
Решение.log6
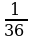 = -2
= -2
Пример 6. Вычислите log
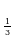 27
27Решение: log
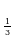 27= -4
27= -4
П Пример 1. Вычислите log2 8
Р Решение: log2 8 = 3.(т.к. 2 3 = 8)
П Пример2. Вычислитеlog5 25.
Р Решение: log5 25 = 2
П Пример 3. Вычислите log224
Р Решение: log224 = 4
римеры решения задач.
-
Самостоятельная работа.
| № | 1 вариант | 2 вариант |
| Вычислите 1. | А) log 3 27 Б) log9 в) log г) log0,2 5 | А) log4 64 б) log7 в) log г) log0,5 2 |
| 2. | А) log98 1 Б) log12 12 В) log9 95
| А) log79 1 Б) log71 71 В) log0,78 0,784
|
| 3. Чему равен х? Запишите ответ с помощью логарифма | А) 3 х = 8 Б) 0,9 х = 23 В) | А) 5 х = 7 Б) 0,8 х = 17 В) |
Практическая работа 5.
Решение практических задач на проценты.
Цели: научиться рассчитывать процент от числа и число по его проценту, использовать знания при решении практических задач
Оборудование: тетрадь для практических работ, ручка, методические рекомендации по выполнению работы
Указание. Практическая работа состоит из двух частей – теоретической и практической. После изучения теоретического материала можно приступать к выполнению практической части. Она состоит из одной или более задач для самостоятельного выполнения. Не забывайте о правильном оформлении решения
Порядок выполнения работы.
-
Рассмотрите теоретический материал по теме и примеры решения задач (приведены ниже).
-
Решите самостоятельную работу. Оформите решение письменно в тетради.
Теоретический материал.
Сотая часть метра - это сантиметр, сотая часть рубля – копейка, сотая часть центнера - килограмм. Люди давно замети, что сотые доли величин удобны в тактической деятельности. Потому для них было придумано специальное название – процент. Значит одна копейка – один процент от одного рубля, а один сантиметр – один процент от одного метра.
Один процент – это одна сотая доля числа. Математическими знаками один процент записывается так: 1%.
Определение одного процента можно записать равенством: 1 % = 0,01 * а
5%=0,05, 23%=0,23, 130%=1,3 и т. д
Как найти 1% от числа? Раз 1% это одна сотая часть, надо число разделить на 100. Деление на 100 можно заменить умножением на 0,01. Поэтому, чтобы найти 1% от данного числа, нужно умножить его на 0,01. А если нужно найти 5% от числа, то умножаем данное число на 0,05 и т.д.
Решение задач профессиональной направленности - это подготовка к применению знаний, таких, как виды процентных вычислений, пропорции, перевод обыкновенных дробей в десятичные и обратно, на практике.
В тех случаях, когда в условии задачи не сказано, относительно какого числа следует вычислять проценты, их следует определить по содержанию задачи:
- отходы при механической кулинарной обработке исчисляются в процентах от массы брутто и, следовательно, масса брутто служит начальным числом;
- потери при тепловой обработке устанавливают, как правило, от массы нетто, так как они получаются при приготовлении продуктов, прошедших механическую обработку, и начальным числом считают массу нетто.
Тема этой работы - процентное вычисление. По данной теме взяты 5 видов задач:
1.Вычисление массы отходов при механической обработке, то есть находим массу нетто: задачи №1, №2, №6, №8.
2.Вычисление массы потери при тепловой обработке: задачи №3, №10.
3.Вычисление массы отходов при механической и тепловой обработке: задачи №4, №7.
4.Разделка мяса - вычисление массы брутто: задача №5.
5.Нахождение процента выполнения выработки плана блюд или товарооборота: задачи №11, №12.
^ Карточка для самостоятельной работы
1.Внимательно прочитай условие задачи.
2.Определи тип задачи.
3.Найди в сборнике задачу похожего типа.
4.Сопоставь данные своей задачи с выбранной задачей.
5. Внимательно изучи образец решения.
6.Правильно оформи решение своей задачи.
Задача №1
Взято для очистки 80 кг картофеля. Определите, какой должна быть масса отходов, если норма отходов установлена 30% массы брутто.
Решение:
Следует найти массу отходов? Начальные 80 кг содержит 100%,масса отходов Х кг содержит 30%. Найдем массу отходов.
80 кг-100%
Х кг-30%
Х=80*30/100=24 кг.
Ответ: 24кг масса отходов.
Задача №2
Масса (нетто) очищенного картофеля 56 кг. Сколько было израсходовано неочищенного картофеля, если норма отходов 30%?
Решение:
Начальным числом является масса брутто. Это искомое число равно 100%. Данное число (масса нетто равна 56 кг) содержит 100%-30%=70% (так как масса нетто равно массе брутто за вычетом массы отходов).Записываем краткое условие задачи: данное число 56 кг содержит 70%,искомое число Х кг - 100%.
56 кг-70%
Х кг-100%
Х=56*100/70=80 кг
Ответ: 80 кг неочищенного картофеля было израсходовано.
Задача №3
Масса очищенного картофеля 56 кг. Потери при тепловой обработки составляет 3% массы нетто. Определите массу вареного картофеля.
Решение:
Следует найти массу вареного картофеля. Данное число (масса 56 кг) содержит 100%-3%=97%.Записывает краткое условие задачи: 56 кг содержит 100%,а Х%-97%.
56кг-100%
Х кг-97%
Х=56*97/100=54,32 кг
Ответ: 54,32 масса вареного картофеля.
Задача №4
На производство поступило 200 кг неочищенного картофеля. Определите, сколько будет получено жареного картофеля, если норма отходов при холодной обработке составляет 30% массы брутто, а потери при тепловой обработке 31% массы нетто.
Решение:
Найдем норму отходов при холодной обработке, которая составляет 30%
200 кг-100%
Х кг – 30%
Х= 200*30/100=60 кг
200-60=140 вес брутто
Найдем массу потери при тепловой обработке
140 кг-100%
Х кг-31%
Х = 140*31/100=43,4
И вычисляем массу жареного картофеля
140-43,4=96,6 кг
Ответ:96,6 кг.
Задача №5
При разделке свинины мясной выход мякоти составляет 86%, отходы 13.5%, потери при разделке 0.5%, определите массу мякоти, отходов и потерь, если масса туши 120кг.
Решение:
Найдем массу мякоти, которая составляет 86%
120 кг- 100%
Х кг-86%
Х= 120*86/100=103,2 –масса мякоти
Найдем массу отходов, которые составляют 13,5%.
120 кг -100%
Х кг- 13,5%
Х=120*13,5/100=16,2-масса отходов
Найдем потери, если их процент при разделки составляет 0,5%
120 кг-100%
Х кг- 0,5%
Х=120*0,5/100=0,6 кг- потери при разделки
Ответ: 103,2 кг-масса мякоти,16,2 кг-масса отходов,0,6-масса потерь.
Задача №6
Масса разделанной говядины 180 кг. Сколько было израсходовано говядины (масса брутто), если норма отходов составляет 26%
Решение: Нужно найти, сколько израсходовано говядины. Выразим чистую массу говядины в процентном состояние. Найдем массу отходов.
100%-26%=74%
180 кг-74%
Х кг-26%
Х= 180*26/74=63,2 кг
Найдем неразделанную говядину сложив разделанную говядину и отходы. 180 + 63,2 =243,2 кг.
Ответ: 243,2 кг.
Задача №7
Масса почек говяжьих охлажденных (брутто) 5 кг. Норма отходов при холодной обработке 7%, потери при варке 47%. Определите массу отварных почек.
Решение: Найдем норму отходов при холодной обработке ,которая составляет 7%.
5 кг-100%
Х кг-7%
Х=5*7/100=0,35 кг-отходов при х/o.
5-0,35=4,65 вес брутто.
Найдем массу потери при варке
4,65 кг-100%
Х кг- 47%
Х=4,65*47/100=2,185 кг потери при варке.
4,65-2,185=2,465 кг
Ответ:2,465 кг масса отварных почек.
Задача №8
Взято для отчистки 80% картофеля. Определите процент отходов при механической обработке, если их масса 24 кг.
Решение:
нужно определить процент отходов, Х кг – это всего картофеля, и это 100%, 24кг-80%.
Хкг-100%
24кг-80%
Х=24*100/80=30%
Ответ: 30% отходов.
Задача №9
Взято для отчистки 80 кг картофеля. После механической обработки получено 56 кг картофеля. Определите процент отходов.
Решение:
Нужно найти процент отходов у нас 80 кг картофеля-100%, 56кг-Х%
80 кг-100%
56-Х%
Х= 56*100/80=70%-это процент при 56 кг, теперь найдем процент при 80 кг картофеля.
100%-70%=30%
Ответ: 30% отходов.
^ Задача №10
Масса очищенного картофеля 56 кг, масса жареного
38 кг640 гр. Определите процент потерь при тепловой обработке.
Решение:
Сначала найдем процент потерь, а потом вычтем из 100% и найдем процент при тепловой обработке.
56 кг-100%
38 кг,640гр –Х%
Х= 38,640*100/56=69 кг
А теперь найдем процент при тепловой обработке
100%-69%=31%
Ответ:31% это потери при тепловой обработке.
^ Задача №11
Определите процент выполнения плана, если план товарооборота 4000 руб., а фактически товарооборот 4008 руб
Решение: Найдем процент выполнения плана 4000-100%,4008-Х%
4000-100%
4008-Х%
Х=4008*100/4000=100,2%
Ответ: 100,2% процент выполнения плана
^ Задача №12
Определите процент выполнения нормы выработки, если фактическая выработка бригады составляет 4950 условных блюд. А плановое задание 5000 блюд.
Решение: Найдем процент выполнения нормы выработки.
5000-100%, 4950-Х%.
5000-100%
4950-Х%
Х=4950*100/5000=99%
Ответ: 99% процент выполнения нормы выработки.
^ Решение задач с помощью таблицы
-
Какое количество картофеля необходимо для приготовления 20 кг картофеля, жаренного ломтиками 18 ноября и 7 апреля? -
Какое количество свеклы столовой (свежей) потребуется для приготовления 7 кг пассированной свеклы в феврале? -
Сколько отходов получится при обработке 10 кг перца свежего сладкого? -
сколько отходов получится при обработке 12 кг огурцов теплично-парниковых и 15 кг огурцов грунтовых? -
Какое количество грибов белых маринованных (в банках) необходимо для 100 порций «Винегрета с грибами», если на одну порцию расходуется 40г грибов массой нетто? -
Сколько необходимо взять свежего лука репчатого для приготовления 35 порций «Бифштекса с луком», если на одну порцию идет 40г лука репчатого пассированного? -
Сколько яблок необходимо для приготовления 50 порций «Яблок с сиропом», если на одну порцию по рецептуре идет 179г яблок свежих? -
Сколько порций «Яблок печеных» получится из 10 кг яблок свежих если для приготовления одной порции необходимо 128г яблок?
^ Расчет расхода сырья, выхода полуфабрикатов и готовых изделий
|
|
|
|
|
| ||||
|
| ||||||||
|
|
|
|
|
| ||||
|
|
|
|
|
| ||||
|
|
|
|
|
| ||||
|
|
|
|
|
| ||||
|
|
|
|
|
| ||||
| Овощи | ||||||||
|
|
|
|
|
| ||||
|
|
|
|
|
| ||||
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Практическая работа 5.
Решение практических задач на проценты.
Цели: научиться рассчитывать процент от числа и число по его проценту, использовать знания при решении практических задач
Оборудование: тетрадь для практических работ, ручка, методические рекомендации по выполнению работы
Указание. Практическая работа состоит из двух частей – теоретической и практической. После изучения теоретического материала можно приступать к выполнению практической части. Она состоит из одной или более задач для самостоятельного выполнения. Не забывайте о правильном оформлении решения
Порядок выполнения работы.
-
Рассмотрите теоретический материал по теме и примеры решения задач (приведены ниже).
-
Решите самостоятельную работу. Оформите решение письменно в тетради.
Теоретический материал
Сотая часть метра - это сантиметр, сотая часть рубля – копейка, сотая часть центнера - килограмм. Люди давно замети, что сотые доли величин удобны в тактической деятельности. Потому для них было придумано специальное название – процент. Значит одна копейка – один процент от одного рубля, а один сантиметр – один процент от одного метра.
Один процент – это одна сотая доля числа. Математическими знаками один процент записывается так: 1%.
Определение одного процента можно записать равенством: 1 % = 0,01 * а
5%=0,05, 23%=0,23, 130%=1,3 и т. д
Как найти 1% от числа? Раз 1% это одна сотая часть, надо число разделить на 100. Деление на 100 можно заменить умножением на 0,01. Поэтому, чтобы найти 1% от данного числа, нужно умножить его на 0,01. А если нужно найти 5% от числа, то умножаем данное число на 0,05 и т.д.
| Дробь | 1/2 | 1/4 | 3/4 | 1/5 | 2/5 | 3/5 | 1/10 | 1/20 | 1/50 |
| Десятичная дробь | 0,5 | 0,25 | 0,75 | 0,2 | 0,4 | 0,6 | 0,1 | 0,05 | 0,02 |
| Проценты | 50% | 25% | 75% | 20% | 40% | 60% | 10% | 5% | 2% |
Пример. Найти: 25% от 120.
Решение:
1) 25% = 0,25;
2) 120 . 0,25 = 30.
Ответ: 30.
Правило 1. Чтобы найти данное число процентов от числа, нужно проценты записать десятичной дробью, а затем число умножить на эту десятичную дробь
Пример. Токарь вытачивал за час 40 деталей. Применив резец из более прочной стали, он стал вытачивать на 10 деталей в час больше. На сколько процентов повысилась производительность труда токаря?
Решение: Чтобы решить эту задачу, надо узнать, сколько, процентов составляют 10 деталей от 40. Для этого найдем сначала, какую часть составляет число 10 от числа 40. Мы знаем, что нужно разделить 10 на 40. Получится 0,25. А теперь запишем в процентах – 25%. Получаем ответ: производительность труда токаря повысилась на 25%.
Правило 2. Чтобы найти, сколько процентов одно число составляет от другого, нужно разделить первое число на второе и полученную дробь записать в виде процентов.
Пример. При плановом задании 60 автомобилей в день завод выпустил 66 автомобилей. На сколько процентов завод выполнил план?
Решение: - такую часть составляют изготовленные автомобили от количества автомобилей по плану. Запишем в процентах =110%
Ответ: 110%
Пример.
На сколько процентов 10 больше 6? 2. На сколько процентов 6 меньше 10?
Решение:
1. ((10 - 6).100%)/6 = 66 2/3 %
2. ((10 - 6).100%)/10 = 40%
Ответ: 66 2/3 %, 40 %.
Пример. Бронза является сплавом олова и меди. Сколько процентов сплава составляет медь в куске бронзы, состоящем из 6 кг олова и 34 кг меди?
Решение: 1) 6+ 34 =40 (кг) масса всего сплава.
2) = 85% сплава составляет медь.
Ответ. 85%.
Пример. Что произойдет с ценой товара, если сначала ее повысить на 25%, а потом понизить на 25%?
Решение: Пусть цена товара х руб, тогда после повышения товар стоит 125% прежней цены, т.е. 1,25х;, а после понижения на 25% , его стоимость составляет 75% или 0, 75 от повышенной цены, т.е. 0,75 *1,25х= 0,9375х, тогда цена товара понизилась на 6, 25 %, т.к. х - 0,9375х = 0,0625х ; 0,0625х/х . 100% = 6,25%
Ответ: первоначальная цена товара снизилась на 6,25%.
Правило 3. Чтобы найти процентное отношение двух чисел А и В, надо отношение этих чисел умножить на 100%, то есть вычислить (а/в)*100%.
Пример. Найти число, если 15% его равны 30.
Решение:
1) 15% = 0,15;
2) 30 : 0,15 = 200.
или: х - данное число; 0,15.х = 300; х = 200.
Ответ: 200.
Пример. Из хлопка-сырца получается 24% волокна. Сколько надо взять хлопка-сырца, чтобы получить 480кг волокна.?
Решение. Запишем 24% десятичной дробью 0,24 и получим задачу о нахождении числа по известной ему части (дроби). 480 : 0,24= 2000 кг = 2 т
Ответ: 2 т
Рассмотрим три основных типа задач на проценты.
Нахождение процента от числа![]()
![]()
![]()
![]()
Чтобы найти процент от числа, нужно число умножить на процент.
Предприятие изготовило за квартал 500 насосов, из которых 60 % имели высшую категорию качества. Сколько насосов высшей категории качества изготовило предприятие?
Решение:
Найдем 60 % от 500 (общее количество насосов).
60 % = 0,6
500 • 0,6 = 300 насосов высшей категории качества.
Ответ: 300 насосов высшей категории качества.
Нахождение числа по его проценту![]()
![]()
![]()
![]()
Чтобы найти число по его проценту, нужно его известную часть разделить на то, сколько процентов она составляет от числа.
Так как задачи «процент по числу» и «число по его проценту» очень похожи и часто не сразу понятно какой тип задачи перед нами, старайтесь внимательно читать текст. Если вам встречаются слова «который», «что составляет» и «который составляет», скорее всего перед вами задача «число по его проценту».
Ученик прочитал 138 страниц, что составляет 23 % числа всех страниц в книге. Сколько страниц в книге?
Решение:
Итак, нам неизвестно сколько всего страниц в книге. Но мы знаем, что часть, которую прочитал ученик (138 страниц) составляет 23 % от общего количества страниц в книге. Так как 138 стр. - это всего лишь часть, само количество страниц, естественно, будет больше 138. Это поможет нам при проверке.
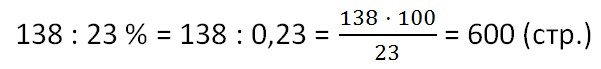
Проверка: 600 138 (это означает, что 138 является частью 600).
Ответ: 600 (стр.) - общее количество страниц в книге.
Сколько процентов одно число составляет от другого![]()
![]()
![]()
![]()
Чтобы найти, сколько процентов одно число составляет от другого, нужно ту часть, о которой спрашивается, разделить на общее количество и умножить на 100 %.
Из 200 арбузов 16 оказались незрелыми. Сколько процентов всех арбузов составили незрелый арбузы?
Решение:
О чем спрашивают? О незрелых арбузах. Значит, 16 делим на общее количество арбузов и умножаем на 100 %.
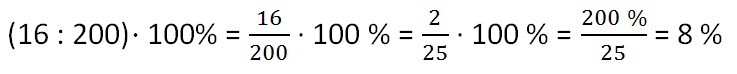
Ответ: 8 % - составляют незрелые арбузы от всех арбузов.
Вкладчик внес в банк 1200 р. В какую сумму вклад превратится через год, если банк начисляет доход в размере 4 % годовых?
Решение:
Найдем какое вознаграждение банк доложит вкладчику. Для этого умножим 1200 р. на процент годовых 4%.
4% = 0,04
1200 • 0, 04 = 48 р. - такое вознаграждение доложит банк вкладчику через год.
Теперь найдем общую сумму, которую заберет вкладчик через год.
1200 + 48 = 1248 р. - в такую сумму превратится вклад через год.
Ответ: 1248 р. - в такую сумму превратится вклад через год.
Задачи на скидку (уценку)Скидка - это понижение цены товара или услуги. Чаще всего скидку указывают в процентах. Поэтому, чтобы найти на сколько в рублях понизилась цена товара, нужно цену товара умножить на процент скидки.
Цена изделия составляет 5000 р. На изделие предложена скидка 10%. Найти цену товара с учетом скидки.
Решение:
Найдем скидку в рублях.
10% = 0,1
5000 • 0,1 = 500 р. - скидка в рублях.
Теперь найдем цену товара с учетом скидки.
5000 - 500 = 4500 р. - цена товара с учетом скидки.
Ответ: 4500 р. - цена товара с учетом скидки.
Для того, чтобы решать задачи на растворы и концентрацию, необходимо чётко понимать, что называется концентрацией раствора.
![]()
![]()
![]()
![]()
Концентрация раствора - это часть, которую составляет масса растворённого вещества от массы всего раствора.
-
9%-я концентрация раствора соли - это 9 грамм соли в 100 граммах раствора.
Килограмм соли растворили в 9 л воды. Чему равна концентрация полученного раствора? (Масса 1 л воды составляет 1 кг)
Используя определение концентрации данное выше, решим задачу следующим образом.
-
1 кг - масса растворённого вещества (соли)
-
9 кг - масса воды в растворе (не путать с общей массой раствора)
-
9 + 1 = 10 кг - общая масса раствора.
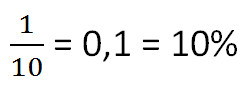
Ответ: 10% - концентрация раствора.
Теперь решим обратную задачу.
№ 353(2)
Сколько соли получится при выпаривании 375 граммов 12%-го раствора?
Чтобы найти массу выпаренной соли из раствора, умножим общую массу раствора на процент концентрации. Не забудем предварительно перевести процент в десятичную дробь.
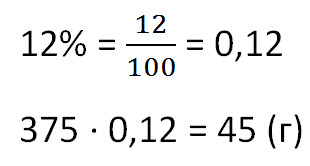
Ответ: 45 г соли.
Сложная задача на растворыВ растворе 40% соли. Если добавить 120 г соли, то процентное содержание соли станет равным 70. Сколько грамм соли было первоначально в растворе?
Для составления пропорции обозначим за x первоначальную массу соли в растворе, а за y массу воды в растворе. Так как концентрация соли в исходном растворе 40%, то соответственно вода составляет
100% - 40%= 60%
Изобразим графически условия задачи.
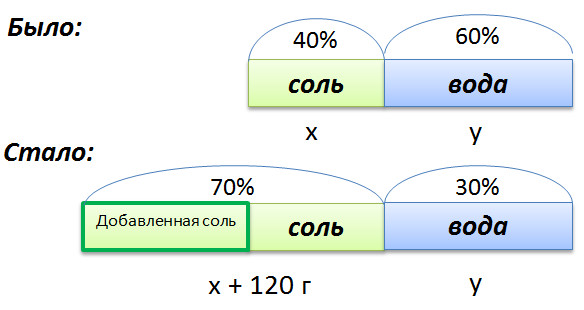
Составим пропорцию, связывающую эти величины до добавления соли.
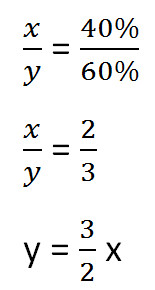
Для решения задачи нам надо определить какая из неизвестных (x или y) остаётся неизменной после добавления соли.
Этой величиной является масса воды в растворе (y).
Выразим её, учитывая изменения в растворе после добавления соли.
-
(x + 120) г - масса соли в новом растворе
-
100% - 70% = 30% - процентное содержание воды в новом растворе.
Составим пропорцию аналогично предыдущей, но с учётом изменений произошедших после добавления соли.
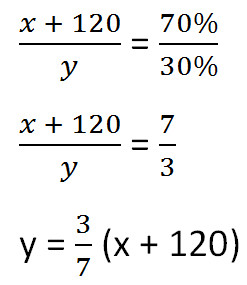
Так как масса воды осталось неизменной после добавления соли, приравняем её значения до и после добавления соли и решим уравнение.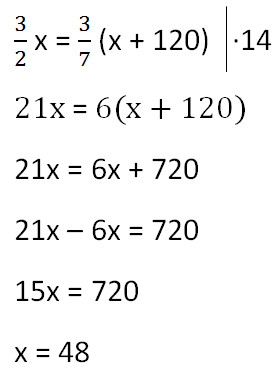
Ответ: 48 г - масса соли в первоначальном растворе
Практическая работа 6.
Свойства степени с действительным показателем.
-
Цели: отработать умение находить значение степени с действительным показателем;
-
закрепить умения использовать свойства степени при упрощении выражений;
-
выработать навык использования свойств степени при вычислениях.
Оборудование: тетрадь для практических работ, ручка, методические рекомендации по выполнению работы
Указание. Практическая работа состоит из двух частей – теоретической и практической. После изучения теоретического материала можно приступать к выполнению практической части. Она состоит из одной или более задач для самостоятельного выполнения. Не забывайте о правильном оформлении решения
Порядок выполнения работы.
-
Рассмотрите теоретический материал по теме и примеры решения задач (приведены ниже).
-
Решите самостоятельную работу. Оформите решение письменно в тетради.
Теоретический материал
Степень с целым показателем
![]() (n раз,
(n раз, ![]() ),
),
![]()
Свойства:
![]()
![]()
Корень n-й степени
![]() - арифметический корень n-й степени из числа
- арифметический корень n-й степени из числа ![]()
![]()
Свойства:
![]()
![]()
В частности, ![]() - арифметический квадратный корень:
- арифметический квадратный корень: ![]()
Степень с дробным (рациональным) показателем
![]()
Свойства степени с действительным показателем
![]()
![]()
![]()
![]()
Примеры решения:
![]() = 2
= 2 ![]() =
= ![]()
![]() =
= ![]()
![]() = 6
= 6 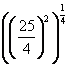 =
= ![]() =
= ![]() ( дес. др.)
( дес. др.)
![]() =
= ![]()
![]() =
= ![]()
Самостоятельная работа
Вычислите  :
: ![]() =
=
Самостоятельно (с проверкой на листах)
 =
=
 =
=
|
|
| 1 | 2 | 3 | 4 |
| 1 |
|
| 25 – | 19 |
|
| 2 |
|
|
| –7 | –9 |
| 3 | 0,3 | 9,1 | 2,9 | 89,9 | 8,9 |
| 4 |
| 1 | 0 | 2,5 | 4 |
11. Задание с кратким ответом (решение у доски):
![]() +
+ ![]() + (60)5
+ (60)5 ![]() 2 – 3–4
2 – 3–4 ![]()
![]()
![]() 27 =
27 =
Самостоятельно с проверкой на скрытой доске:
![]() –
– ![]() – 32
– 32![]() 2– 4
2– 4![]()
![]() + (30)4
+ (30)4 ![]() 4 =
4 =
12. Сократите дробь (на доске):
![]() =
=
1. Укажите выражение, равное степени ![]()
| 1. | 2. | 3. | 4. |
2. Представьте в виде степени произведение: ![]()
| 1. | 2. | 3. | 4. |
3. Упростите выражение ![]() :
: ![]() и найдите его значение при х = 2
и найдите его значение при х = 2
| 1. | 2. 8 | 3. | 4. – 8 |
4. Чему равно значение выражения ![]() при а =
при а = ![]()
| 1. – 9 | 2. | 3. | 4. 9 |
5. Вычислите ![]()
| 1. | 2. | 3. 16 | 4. – 16 |
6.. 
7. Упростите выражение 
8.Сравните числа  и
и 
Практическая работа 8.
Переход логарифма к новому основанию.
Цели: научиться рассчитывать процент от числа и число по его проценту, использовать знания при решении практических задач
Оборудование: тетрадь для практических работ, ручка, методические рекомендации по выполнению работы
Указание. Практическая работа состоит из двух частей – теоретической и практической. После изучения теоретического материала можно приступать к выполнению практической части. Она состоит из одной или более задач для самостоятельного выполнения. Не забывайте о правильном оформлении решения
Порядок выполнения работы.
-
Рассмотрите теоретический материал по теме и примеры решения задач (приведены ниже).
-
Решите самостоятельную работу. Оформите решение письменно в тетради.
Теоретический материал
Определение. Логарифмом положительного числа b по положительному и отличному от единицы основанию а называют показатель степени, в которую надо возвести число
а, чтобы получить b.
loga b = x, ax = b ( b 0, a ≠ 1) ,
а logab = b – основное логарифмическое тождество.
-
loga a = 1
-
loga 1 = 0
-
loga ас = с.
Операция нахождения логарифма числа называют логарифмированием. Эта операция является обратной по отношению к возведению в степень.
Пример . 42 = 16, log4 16 = 2
Логарифмом по основанию 10 называют десятичным логарифмом. Вместо символа log10 принято использовать символ lg
Свойства логарифмов.
loga bc = loga b + loga c ( b 0 , c 0)
loga 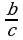 = loga b - loga c ( a 0, b 0, c 0)
= loga b - loga c ( a 0, b 0, c 0)
loga bk = k loga b ( b 0)
logak b = 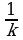 loga b
loga b
loga x = 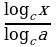 (с 0, с ≠ 1) формула перехода к новому основанию.
(с 0, с ≠ 1) формула перехода к новому основанию.
loga b = 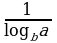
loga b = logar br
Примеры решения:
| Задание. | Найти значение выражения |
| Решение. | В первом логарифме разложим подлогарифмическую функцию - 15 - на множители и применим к полученному логарифму свойство суммы логарифмов, во втором воспользуемся свойством степени основания:
Учитывая, что
|
| Ответ. |
|
| Задание. | Доказать тождество |
| Доказательство. | Преобразуем все логарифмы в левой части выражения к одному основанию, в качестве которого возьмем, например, 2. Используя формулу для замены основания логарифма:
Получим следующее выражение:
К логарифму в знаменателе применим свойство логарифма степени и, учитывая, что
|
|
| Что и требовалось доказать. |
| Задание. | Доказать тождество |
| Доказательство. | Доказательство будем проводить на основе формул и свойств логарифмов описанных на нашем сайте. Используя следствие из формулы замены основания логарифма, а именно, что
преобразуем логарифмы в левой части заданного выражения к логарифмам по основанию
Логарифм произведения, стоящий в числителе, согласно свойству заменим суммой логарифмов от каждого из сомножителей. В результате будем иметь:
Полученную дробь, используя формулу замены основания логарифма
преобразуем к виду:
|
|
| Что и требовалось доказать. |
| Задание. | Доказать тождество: |
| Доказательство. | Приведем все логарифмы, стоящие в правой части приведенного равенства к одному основанию 3, используя формулу для замены основания логарифма:
тогда выражение примет вид:
Учитывая тот факт, что
Согласно свойству суммы логарифмов получаем окончательный ответ
В итоге:
|
|
| Что и требовалось доказать. |
| Задание. | Доказать тождество: |
| Доказательство. | Используя следствие из формулы замены основания логарифма, а именно, что
преобразуем все логарифмы в правой части заданного выражения к логарифмам по основанию Сначала числитель дроби:
Затем знаменатель:
Следовательно, выражение в правой части преобразуется в
В последнем выражении в знаменателе, применяя сначала свойство суммы логарифмов, а затем следствие из формулы замены основания логарифма, получим
|
|
| Что и требовалось доказать. |
Практическая работа 9.
Способы задания плоскости.
Цели: рассмотреть условия задания плоскости и научиться задавать единственную плоскость в пространстве
Оборудование: тетрадь для практических работ, ручка, методические рекомендации по выполнению работы
Указание. Практическая работа состоит из двух частей – теоретической и практической. После изучения теоретического материала можно приступать к выполнению практической части. Она состоит из одной или более задач для самостоятельного выполнения. Не забывайте о правильном оформлении решения
Порядок выполнения работы.
-
Рассмотрите теоретический материал по теме и примеры решения задач (приведены ниже).
-
Решите самостоятельную работу. Оформите решение письменно в тетради.
Все возможные способы задания плоскости в пространстве представлены в следующей таблице.
| Фигура | Рисунок | Тип утверждения и формулировка |
| Три различные точки |
| Аксиома о плоскости, заданной тремя точками. Через три различные точки в пространстве проходит одна и только одна плоскость. |
| Прямая линия и точка, не лежащая на этой прямой |
| Теорема о плоскости, определяемой прямой и точкой. Через прямую и точку, не лежащую на этой прямой, проходит одна и только одна плоскость. |
| Две пересекающиеся прямые |
| Теорема о плоскости, определяемой двумя пересекающимися прямыми. Через две пересекающиеся прямые проходит одна и только одна плоскость, содержащая обе эти прямые. |
| Две параллельные прямые |
| Теорема о плоскости, определяемой двумя параллельными прямыми. Через две параллельные прямые проходит одна и только одна плоскость, содержащая обе эти прямые. |
Утверждение. Через любую прямую в пространстве проходит бесконечно много плоскостей (рис.5).

Рис.1
Замечание. Через любые две скрещивающиеся прямые не проходит ни одной плоскости.
Практическая работа 10.
Расположение прямых в пространстве.
Цели: научиться задавать и определять положение прямых в пространстве
Оборудование: тетрадь для практических работ, ручка, методические рекомендации по выполнению работы
Указание. Практическая работа состоит из двух частей – теоретической и практической. После изучения теоретического материала можно приступать к выполнению практической части. Она состоит из одной или более задач для самостоятельного выполнения. Не забывайте о правильном оформлении решения
Порядок выполнения работы.
-
Рассмотрите теоретический материал по теме и примеры решения задач (приведены ниже).
-
Решите самостоятельную работу. Оформите решение письменно в тетради.
Теоретический материал
Признак скрещивающихся прямых.
Угол между скрещивающимися прямыми Взаимное расположение двух прямых в пространстве
Все возможные случаи взаимного расположения двух прямых в пространстве представлены в следующей таблице.
| Фигура | Рисунок | Определение |
| Две пересекающиеся прямые |
| Две прямые называют пересекающимися прямыми, если они имеют единственную общую точку. |
| Две параллельные прямые |
| Две прямые называют параллельными прямыми, если они лежат в одной плоскости и не имеют общих точек |
| Две скрещивающиеся прямые |
| Две прямые называют скрещивающимися прямыми, если не существует плоскости, содержащей обе прямые. |
С перечисленными в предыдущей таблице случаями взаимного расположения двух прямых в пространстве близко связаны утверждения, представленные в следующей таблице.
| Фигура | Рисунок | Тип утверждения и формулировка |
| Две различные точки |
| Аксиома о прямой линии, заданной двумя точками |
| Прямая линия и точка, не лежащая на этой прямой |
| Аксиома о параллельных прямых |
| Две пересекающиеся прямые |
| Теорема о плоскости, определяемой двумя пересекающимися прямыми |
| Две параллельные прямые |
| Теорема о плоскости, определяемой двумя параллельными прямыми |
Признак скрещивающихся прямых. Если одна из двух прямых лежит на плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещиваются (рис.1).
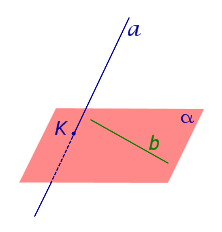
Рис.1
Доказательство. Напомним, что две прямые называют скрещивающимися, если не существует плоскости, содержащей обе эти прямые, и будем доказывать признак скрещивающихся прямых методом «От противного».
Для этого предположим, что прямая a, пересекающая плоскость в точке K, и прямая b, лежащая в плоскости α (рис. 1), не являются скрещивающимися. Из этого предположения следует, что существует плоскость, содержащая обе эти прямые. Обозначим эту плоскость буквой β и докажем, что плоскость β совпадает с плоскостью α. Действительно, поскольку обе плоскости α и β проходят через прямую b и точку K, не лежащую на этой прямой, то они совпадают. Следовательно, прямая a лежит в плоскости. Мы получили противоречие с тем, что по условию прямая a пересекает плоскость, а не лежит в ней. Доказательство признака скрещивающихся прямых завершено.
Угол между скрещивающимися прямымиУглом между скрещивающимися прямыми называют угол между пересекающимися прямыми, соответственно параллельными данным скрещивающимся прямым (рис. 2).
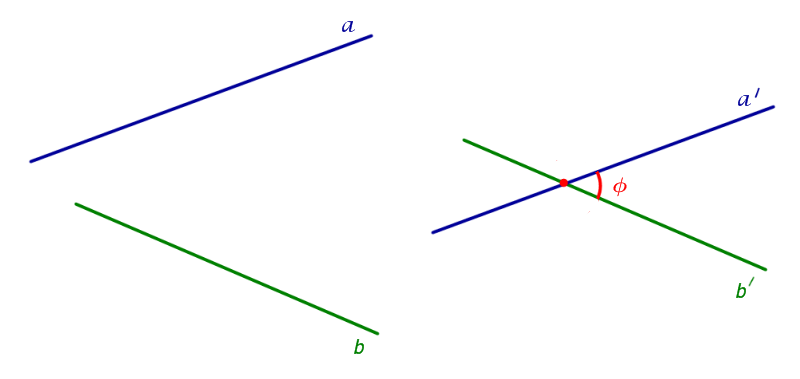
Рис.2
На рисунке 2 изображены скрещивающиеся прямые a и b. Прямая a' параллельна прямой a, прямая b' параллельна прямой b. Прямые a' и b' пересекаются. Угол φ и является углом между скрещивающимися прямыми a и b.
Задача. В кубе ABCDA1B1C1D1 найти угол между прямыми AB1 и BC1.
Решение. Поскольку прямая AB1 пересекает плоскость BB1C1 в точке B1, которая не лежит на прямой BC1, то по признаку скрещивающихся прямых прямые AB1 и BC1 скрещиваются (рис. 3).
Рис.3
Для того, чтобы найти угол между прямыми AB1 и BC1, проведем в кубе диагональ боковой грани
AD1 и диагональ верхнего основания D1B1 (рис. 4).
Практическая работа 11.
Признак параллельности прямых в пространстве.
Цели: научиться задавать и определять положение параллельных прямых в пространстве
Оборудование: тетрадь для практических работ, ручка, методические рекомендации по выполнению работы
Указание. Практическая работа состоит из двух частей – теоретической и практической. После изучения теоретического материала можно приступать к выполнению практической части. Она состоит из одной или более задач для самостоятельного выполнения. Не забывайте о правильном оформлении решения
Порядок выполнения работы.
-
Рассмотрите теоретический материал по теме и примеры решения задач (приведены ниже).
-
Решите самостоятельную работу. Оформите решение письменно в тетради.
Теоретический материал
Признак параллельности прямых в пространстве
Теорема
Две прямые , параллельные третьей прямой, параллельны.
Доказательство
Пусть прямые b и с параллельны прямой a. Нужно доказать, что прямые b и с параллельны.
Случай, когда прямые a, b, с лежат в одной плоскости рассмотрен а разделе параллельные прямые.
Пусть прямые не лежат в одной плоскости и β - плоскость, в которой лежат прямые a и b, а γ - плоскость, в которой лежат прямые a и с. Плоскости β и γ различны. Отметим на прямой b какую-нибудь точку B и проведем плоскость γ1 через прямую с и точку B. Она пересечет плоскость β по прямой b1.
Прямой b1 не пересекает плоскость γ. Действительно, точка пересечения должна принадлежать прямой a, так как прямая b1 лежит в плоскости β. С другой стороны, она должна лежать и на прямой с, так как прямая b1 лежит в плоскости γ1. Но прямые a и с как параллельные не пересекаются.
Так как прямая b1 лежит в плоскости β и не пересекает прямую a, то она параллельна a, а значит, совпадает с b по аксиоме параллельных. Значит, прямая b, совпадая с прямой b1, лежит в одной плоскости с прямой с (в плоскости γ1) и не пересекает ее и прямы е b и с параллельны.
Теорема доказана.
|
Поделиться
Кнопка сайта ЛГ МБОУ "СОШ № 5"
Сетевой город
ГИА математика
ЕГЭ математика
|
Взаимное расположение прямых и плоскостей в пространстве.
Способы определения плоскости.
Из аксиом стереометрии и их следствий получаем 4 способа задания плоскости.
Плоскость единственным образом может быть определена:
| Через любые 3 точки пространства, не лежащие на одной прямой проходит плоскость, и при том только одна.
| Через прямую и не лежащую на ней точку проходит плоскость, и при том только одна. | Через две пересекающиеся прямые проходит плоскость, и при том только одна.
| Через две параллельные прямые проходит плоскость, и при том только одна. |
![]()
Параллельные прямые в пространстве.
Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной и при том только одна.
| Если одна из параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость. | |
| Если две прямые параллельны третьей прямой, то они параллельны. | |
![]()
Взаимное расположение прямой и плоскости в пространстве.
|
| Общие точки | Взаимное расположение |
|
| Более одной | Прямая лежит в плоскости |
|
| Только одна | Прямая пересекает плоскость |
|
| Ниодной | Прямая и плоскость параллельны |
![]()
Параллельность прямой и плоскости.
Признак параллельности прямой и плоскости:
Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.
| Если плоскость проходит через данную прямую, параллельнуй другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой. |
|
| Если одна из двух паралельных прямых параллельна, то другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости. |
|
Полезное для учителя




 е.
е.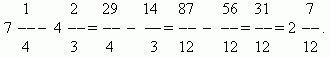
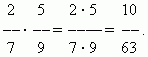
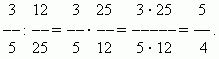
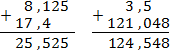
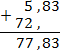
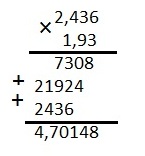
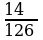 ;
; 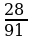 ;
; 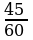
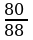 ;
;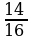 ;
; 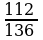
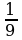 и
и 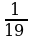 ;
; 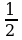 и
и 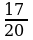
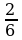 и
и 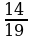 ;
; 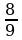 и
и 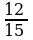
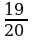 -
- 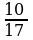 ;
; ;
;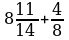
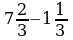
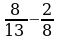
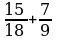
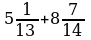
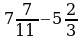
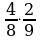
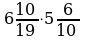
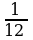 :
: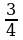
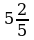 :
: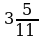
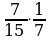
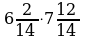
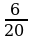 :
: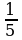
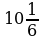 :
: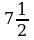
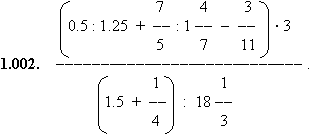
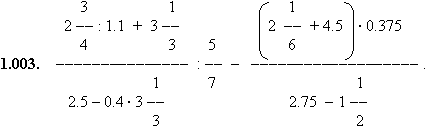
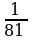
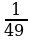
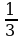 81
81