ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ЛУГАНСКОЙ НАРОДНОЙ РЕСПУБЛИКИ
"КИРОВСКАЯ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА №3"
Практическая работа
урока информатики
Тема: “ Экспертные оценки при анализе системы. Ранговая корреляция и конкордация”
Составитель: учитель информатики II категории
Петров Денис Сергеевич
2017 г.
Цель: научиться определять статистические параметры экспертных оценок при анализе системы.
Задание:
Задание 1
Двумя экспертами А и В проведена оценка группы из 10 изделий. Этим изделиям присвоены номера от 1 до 10. Эксперты проранжировали их в порядке убывания качества. Результаты оценки представлены в таблице.
Нужно найти коэффициенты ранговой корреляции Спирмена и Кенделла и сделать выводы о совпадении мнений двух экспертов.
| Факторы | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Ранжирование эксперта А | 1 | 3 | 5 | 7 | 2 | 4 | 6 | 8 | 10 | 9 |
| Ранжирование эксперта В | 4 | 5 | 1 | 2 | 3 | 7 | 6 | 9 | 10 | 8 |
Задание 2
Пусть у нас есть ранжирование 5 экспертов по отношению к 7 факторам, которые определяют эффективность некоторой системы. Найти коэффициент конкордации и сделать вывод о согласованности мыслей экспертов.
| Факторы Эксперты | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| A | 4 | 5 | 1 | 7 | 6 | 2 | 3 |
| B | 3 | 2 | 1 | 6 | 7 | 4 | 5 |
| C | 4 | 1 | 7 | 3 | 5 | 2 | 6 |
| D | 4 | 3 | 1 | 2 | 5 | 6 | 7 |
| Е | 3 | 2 | 6 | 4 | 1 | 7 | 5 |
Задание 3
Для вычисления одного из коэффициентов корреляции или коэффициента конкордации составить программу на любом языке программирования. Сравнить результаты расчетов по этой программе с вычисленным Вами значениями.
Выполнение работы
Таблица №1
| Факторы | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Сумма |
| Ранжирование эксперта А | 1 | 3 | 5 | 7 | 2 | 4 | 6 | 8 | 10 | 9 | 55 |
| Ранжирование эксперта В | 4 | 5 | 1 | 2 | 3 | 7 | 6 | 9 | 10 | 8 | 55 |
| Сумма рангов | 5 | 8 | 6 | 9 | 5 | 11 | 12 | 17 | 20 | 17 |
|
| Суммарный ранг | 1,5 | 4 | 3 | 5 | 1,5 | 6 | 7 | 8,5 | 10 | 8,5 | 55 |
Проще в реализации является первый - вычисляется значение коэффициента Спирмена
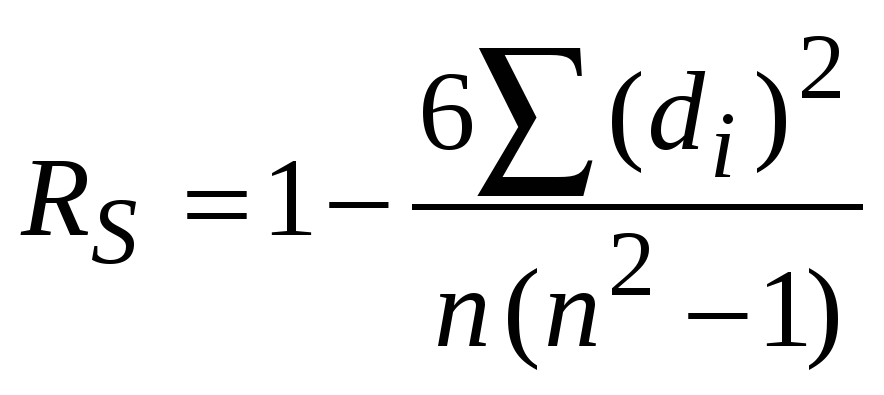
где 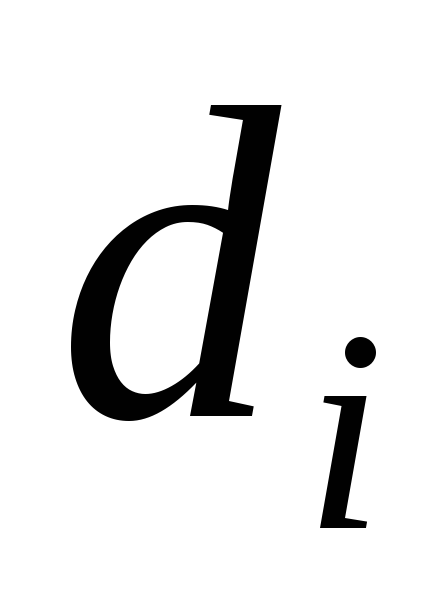 определяются различиями рангов первого и второго ранжирований по объектам в каждой.
определяются различиями рангов первого и второго ранжирований по объектам в каждой.
Таблица №2
| Факторы | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Сумма |
| А | 1 | 3 | 5 | 7 | 2 | 4 | 6 | 8 | 10 | 9 | 55 |
| В | 4 | 5 | 1 | 2 | 3 | 7 | 6 | 9 | 10 | 8 | 55 |
| Разница рангов | -3 | -2 | 4 | 5 | -1 | -3 | 0 | -1 | 0 | 1 |
|
| Квадрат разницы рангов | 9 | 4 | 16 | 25 | 1 | 9 | 0 | 1 | 0 | 1 | 66 |
В нашем примере сумма квадратов разностей рангов составляет 66, а коэффициент корреляции Спирмена равен:
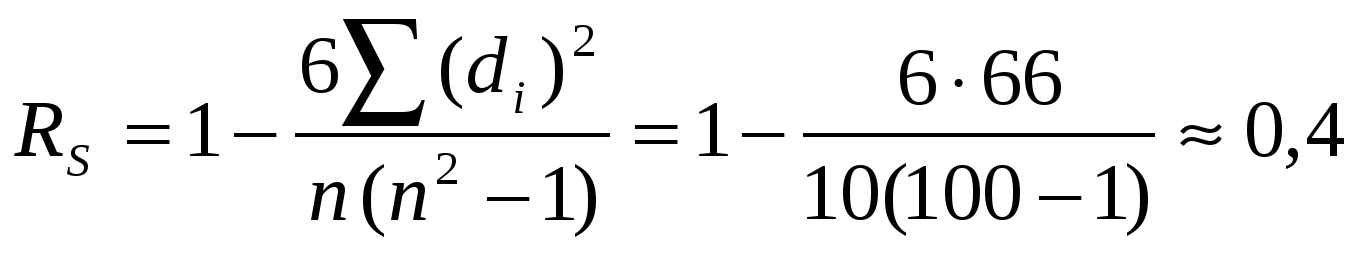
что дает основание утверждать о том, что оценки экспертов имеют недостаточно хорошее совпадение...
Следует отметить, что статистика
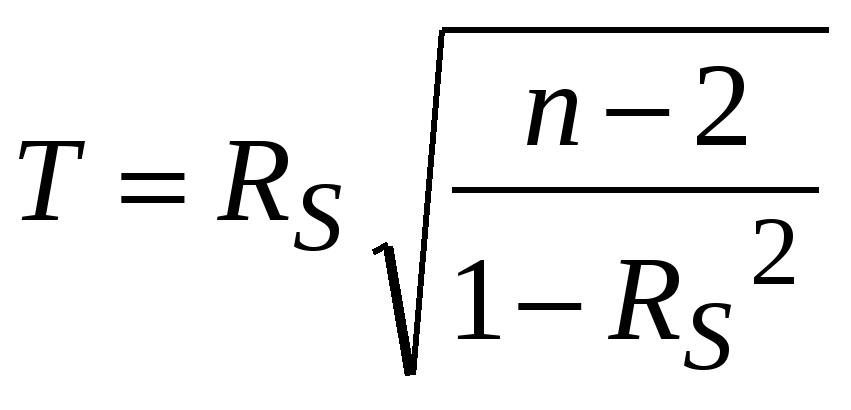 при
при 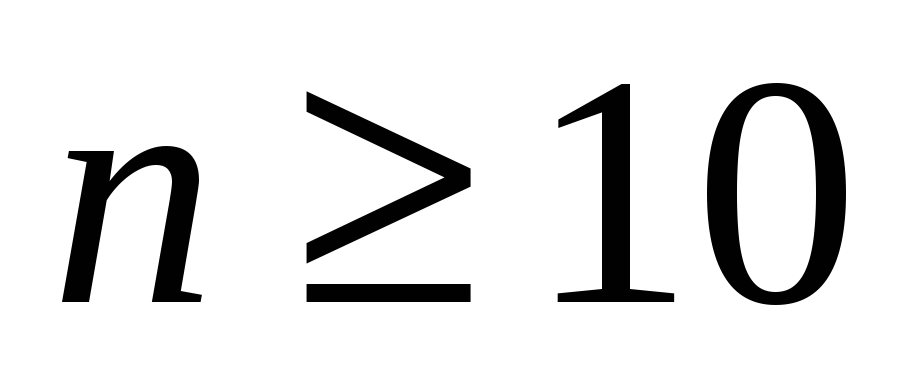
приближенно имеет 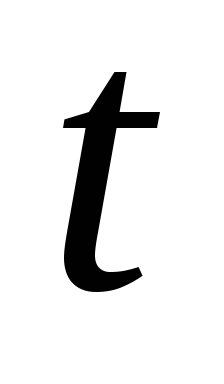 -распределение с
-распределение с 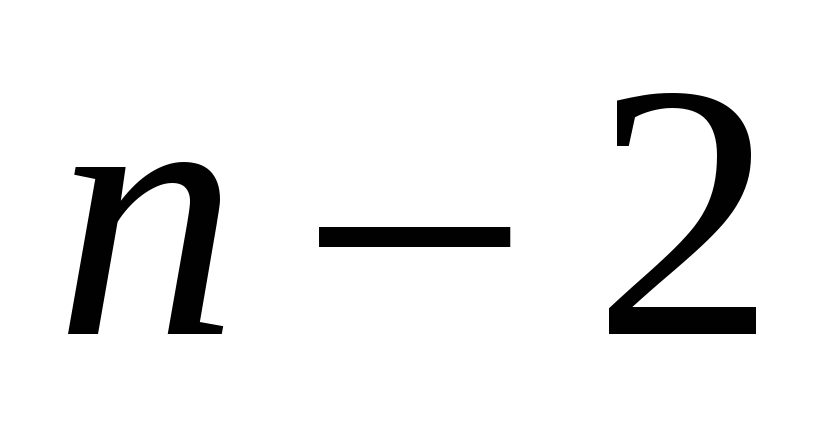 степенями свободы и значение вероятности гипотезы о полной независимости два ранжирования для нашего примера составляет всего лишь 0,004.
степенями свободы и значение вероятности гипотезы о полной независимости два ранжирования для нашего примера составляет всего лишь 0,004.
Коэффициент Кенделла вычисляется по формуле
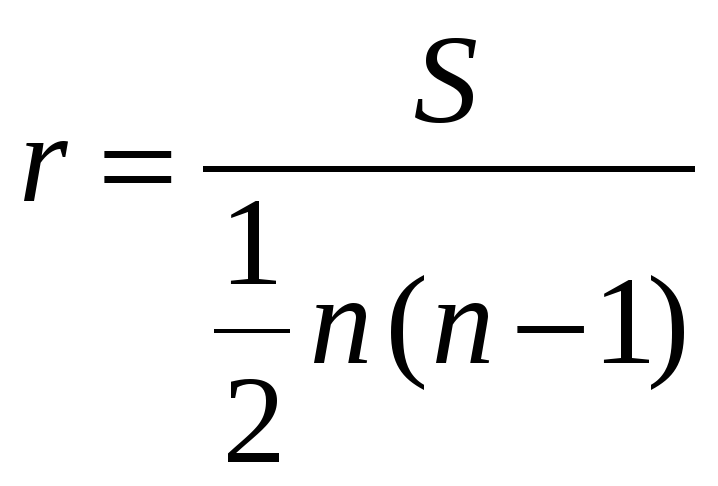
где 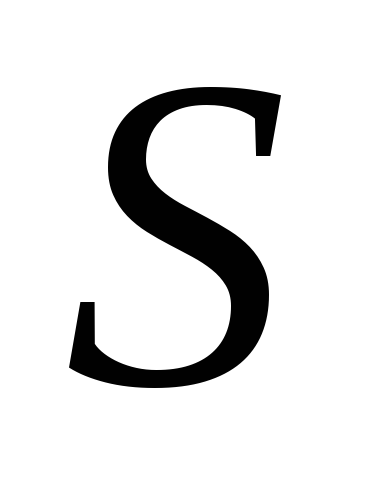 - общая сумма инверсий всех оценок экспертов. Если все ранги в двух экспертов совпадают, то,
- общая сумма инверсий всех оценок экспертов. Если все ранги в двух экспертов совпадают, то, 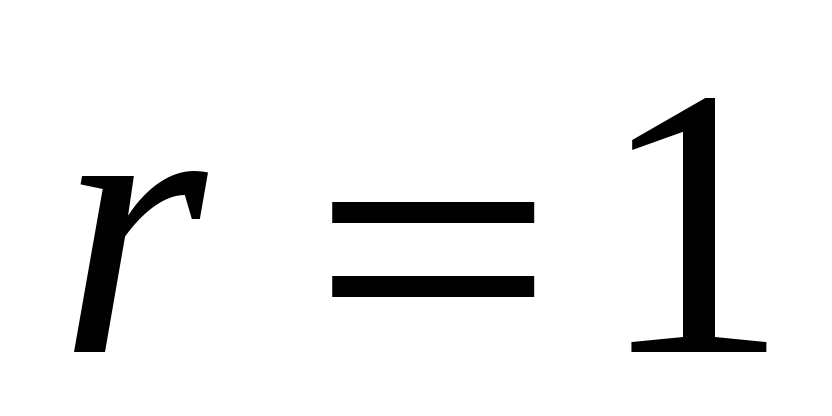 , если они противоположны, то
, если они противоположны, то 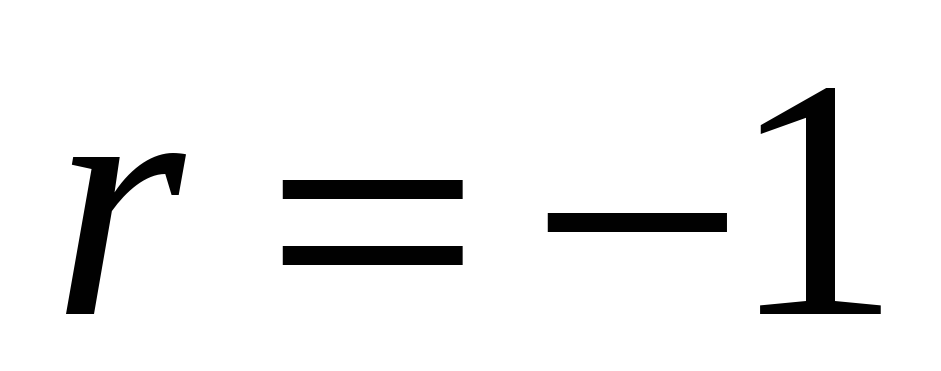 . Кроме того, если учитывать только негативные инверсии оценок, а их сумму обозначить
. Кроме того, если учитывать только негативные инверсии оценок, а их сумму обозначить 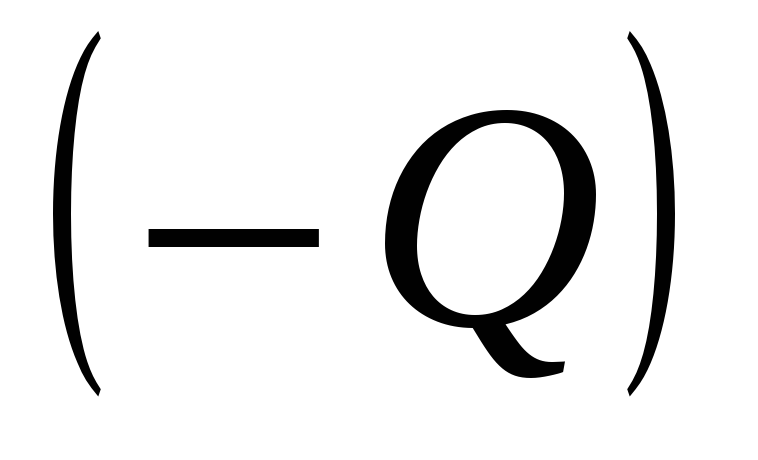 , то коэффициент Кенделла
, то коэффициент Кенделла 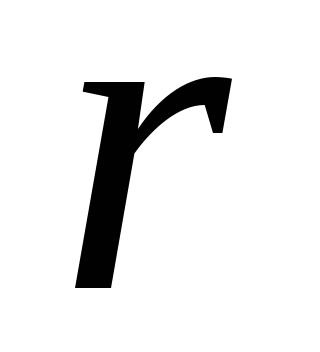 можно рассчитать по формуле
можно рассчитать по формуле
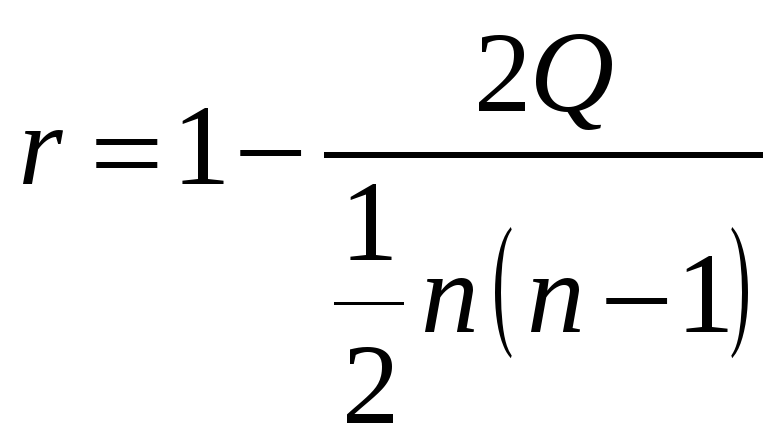
Для того, чтобы вычислить этот коэффициент, следует переписать таблицу оценок экспертов так, чтобы данные ранжирования А были упорядочены по возрастанию: 1, 2, 3, 10, а под ними соответствующие им результаты ранжирования В
Таблица №3
| Фактори | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Ранжирование эксперта А | 1 | 3 | 5 | 7 | 2 | 4 | 6 | 8 | 10 | 9 |
| Ранжирование эксперта В | 4 | 5 | 1 | 2 | 3 | 7 | 6 | 9 | 10 | 8 |
Таблица №4
| Фактори | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Ранжирование эксперта А | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Ранжирование эксперта В | 4 | 3 | 5 | 7 | 1 | 6 | 2 | 9 | 8 | 10 |
Затем на основании этой таблицы подсчитывают (только для данных В), последовательно начиная слева:
число данных дело, которые менее 4 - 3;
число данных дело, которые менее 3 - 2;
число данных дело, которые менее 5 - 2;
число данных дело, которые менее 7 - 3;
число данных дело, которые меньше 1 - 0;
число данных дело, которые менее 6 - 1;
число данных дело, которые менее 2 - 0;
число данных дело, которые менее 9 - 1;
число данных дело, которые менее 8 - 0;
число данных дело, которые меньше 10 - 0;
Далее подсчитываем сумму инверсий
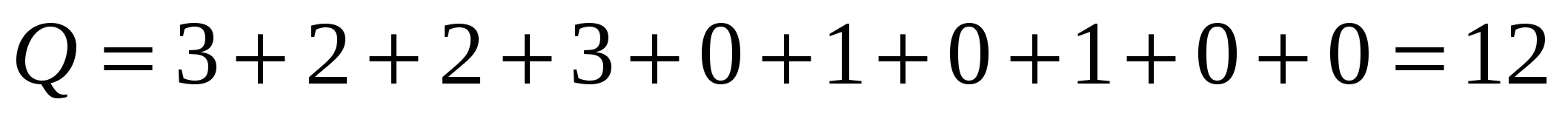 .
.
Отсюда
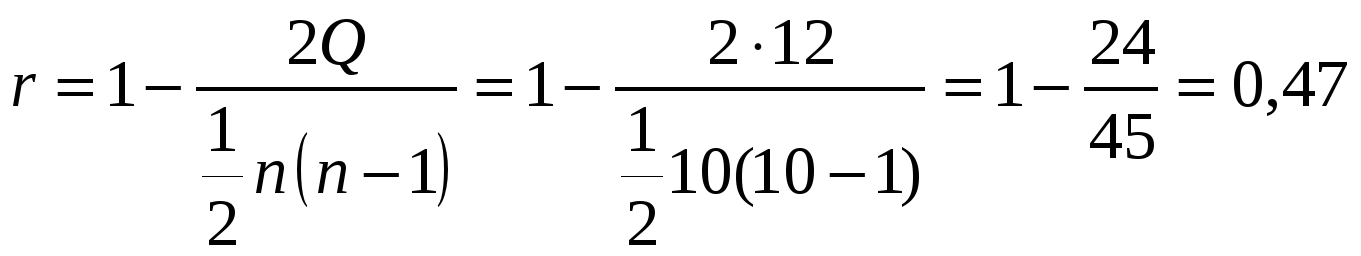 .
.
Результат говорит о недостаточной степени согласованности мнений экспертов.
Задание 2
Пусть у нас есть ранжирование 5 экспертов по отношению к 7 факторам, которые определяют эффективность некоторой системы. Найти коэффициент конкордации и сделать вывод о согласованности мыслей экспертов.
| Факторы Эксперты | 1 | 2 | 3 | 4 | 5 | 6 | 7 | Сумма |
| A | 4 | 5 | 1 | 7 | 6 | 2 | 3 | 28 |
| B | 3 | 2 | 1 | 6 | 7 | 4 | 5 | 28 |
| C | 4 | 1 | 7 | 3 | 5 | 2 | 6 | 28 |
| D | 4 | 3 | 1 | 2 | 5 | 6 | 7 | 28 |
| Е | 3 | 2 | 6 | 4 | 1 | 7 | 5 | 28 |
| Сумма рангов Суммарный ранг | 18 3 | 13 1 | 16 2 | 22 5 | 24 6 | 21 4 | 26 7 | 140 |
| Отклонение суммы от среднего | -2 4 | -7 49 | -4 16 | +2 4 | +4 16 | +1 1 | +6 36 |
126 |
Заметим, что полная сумма рангов составляет 140, дает в среднем по 20 на фактор. Для общего случая 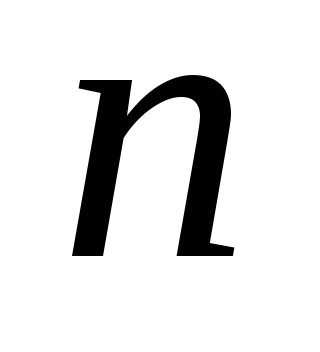 -факторов и
-факторов и 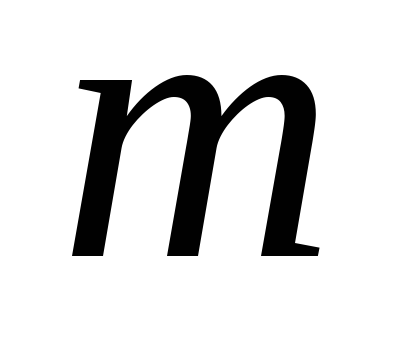 -экспертов среднее значение суммы рангов для любого фактора определится выражением.
-экспертов среднее значение суммы рангов для любого фактора определится выражением.
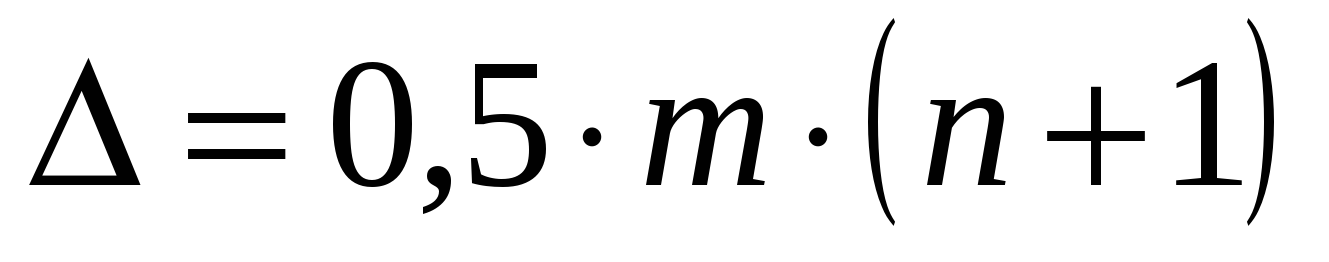
Теперь можно оценить степень согласованности мнений экспертов по отношению к шести факторам. Для каждого из факторов наблюдается отклонение суммы рангов, указанных экспертами, от среднего значения такой суммы. Поскольку сумма отклонений всегда равна нулю, для их усреднения разумно использовать квадраты значений.
В нашем случае сумма таких квадратов составит S = 126, а в общем случае эта сумма будет наибольшей только при полном совпадении мнений всех экспертов по отношению ко всем факторам:
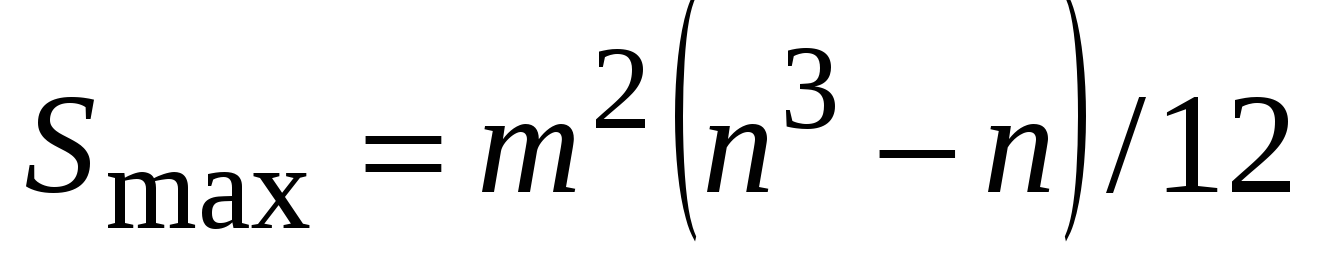
М. Кенделлом предложен показатель согласованности или коэффициент конкордации, определяющийся как
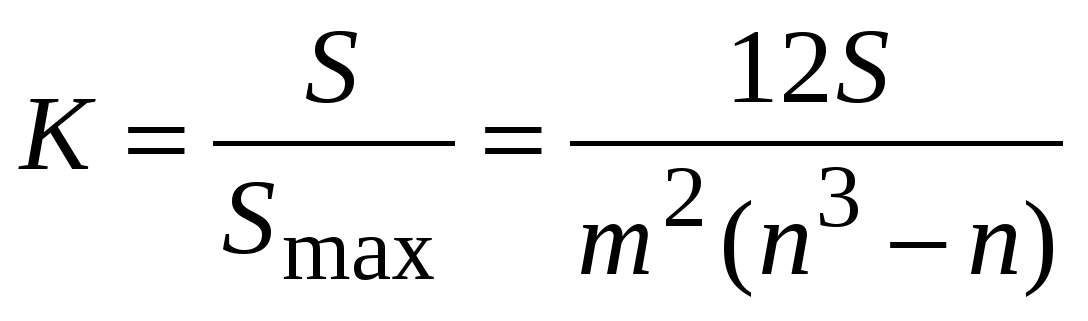
В нашем примере значение коэффициента конкордации составляет
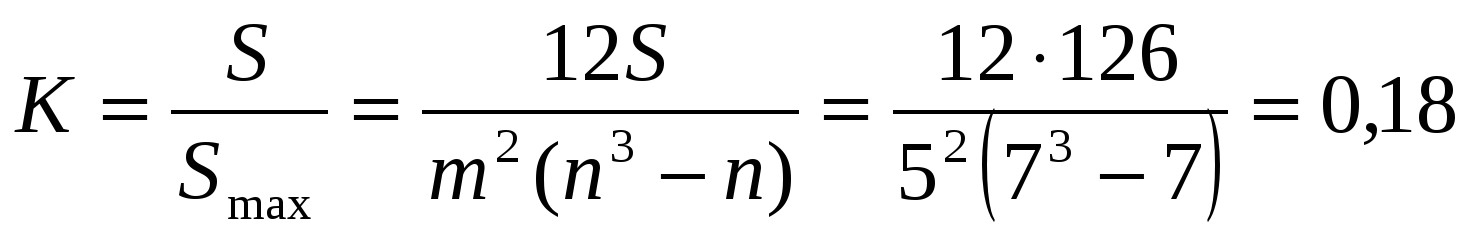 ,
,
что при пяти экспертах и семи факторах достаточно, чтобы считать мнения экспертов несогласованными (с вероятностью не более 0,05). Дело в том, что как раз случайность ранжирований, их некоррелятивность просчитывается достаточно просто. Так для нашего примера указана вероятность соответствует сумме квадратов отклонений  = 126,2.
= 126,2.







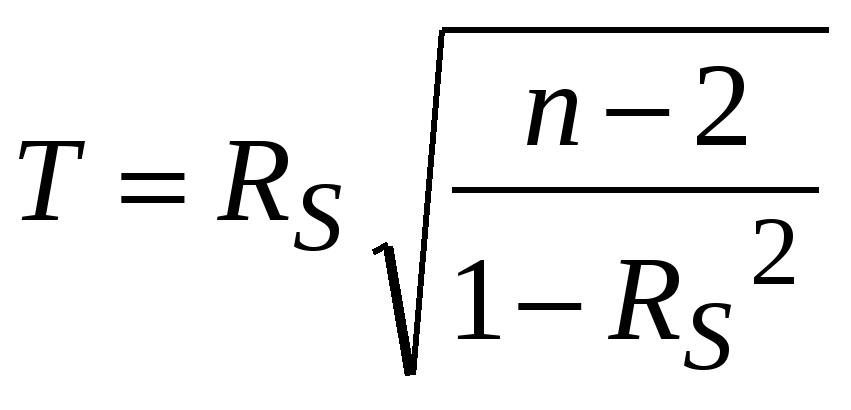 при
при 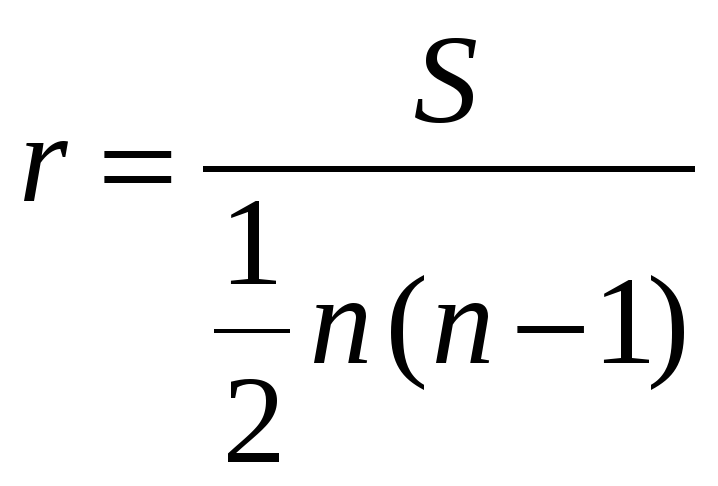
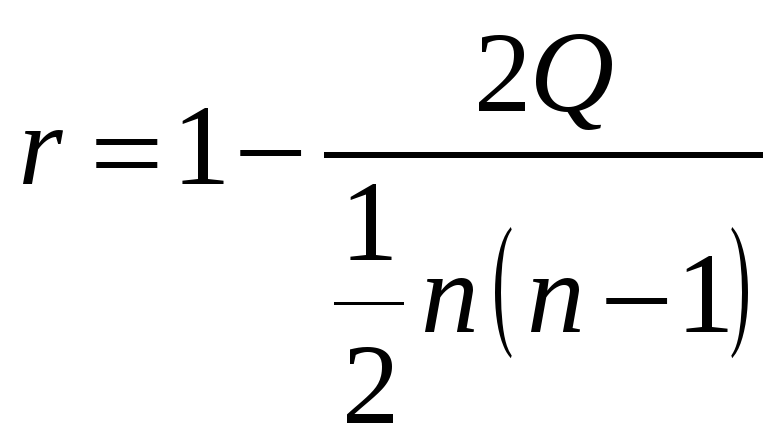
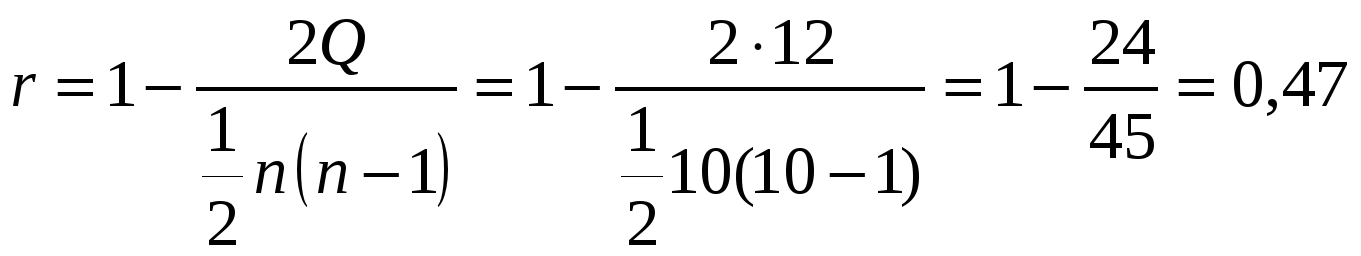 .
.




















