РОСЖЕЛДОР
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Ростовский государственный университет путей сообщения»
(ФГБОУ ВО РГУПС)
Волгоградский техникум железнодорожного транспорта
(ВТЖТ – филиал РГУПС)
Практические занятия
Дисциплина
Математика
для специальности
23.02.06 Техническая эксплуатация подвижного состава
железных дорог
Преподаватель Марченко Л.Е.
Практическая работа № 1
«Нахождение полного сопротивления электрической цепи
переменного тока с помощью комплексных чисел».
Цели занятия:
1) Систематизировать и обобщить знания студентов в области комплексных чисел;
2) Выработать навыки и умения применять теорию комплексных чисел в решении физических задач;
3) Развивать умения пользоваться опорным конспектом и дидактическим материалом для постановки задачи и её выполнения в ходе решения;
4) Воспитывать ответственное отношение к учебному труду, настойчивости для достижения конечных результатов.
Ход работы
Расчет линейных электрических схем переменного тока аналогичен расчету электрических схем постоянного тока. В обоих случаях составляют систему алгебраических уравнений по методам, основанным на законах Ома и Кирхгофа.
Для схем постоянного тока уравнения составляют по действительным значениям напряжений, токов, сопротивлений и проводимостей. В схемах же переменного тока для уравнений применяют комплексные (символические) величины: U, I, Z=R+ jX. При этом все параметры записывают в виде комплексных чисел в алгебраической показательной или тригонометрической форме. При переходе от интегрально-дифференциальных уравнений дифференцирование мгновенного значения заменяют умножением jω на соответствующую комплексную величину, а интегрирование — делением комплексной величины на jω:


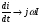

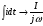
если i = Im cos (ωt +φ).
Полученную систему алгебраических уравнений решают относительно неизвестного комплексного параметра, например, тока I=Imеjφ. При необходимости совершают переход от комплексной величины к ее мгновенному значению.
Алгоритм расчета комплексным методом
1. Мгновенные значения напряжений источников э. д. с, токов источников тока заменяют соответствующими комплексными значениями, например, u= Um cos (ωt + φ) заменяют U = Um ejφ, i = Im cos (ωt + φ) заменяют I = Imejφ.
2. Комплексные сопротивления Z = R + jX всех ветвей схемы записывают в зависимости от выбранного метода расчета.
3. Алгебраические уравнения решают относительно искомой комплексной величины, например, тока I = Imejφ.
4. При необходимости переходят к мгновенному значению i = Im cos (ωt + φ).
В любой момент времени сумма мгновенных значений напряжений на последовательно включенных элементах цепи равна мгновенному значению приложенного напряжения (Рис. 1):
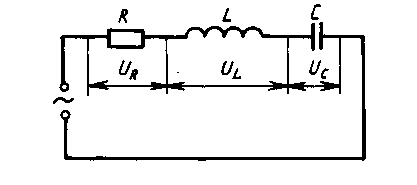
Рис. 1.
u = uR +uL +ис.
Во всех последовательно включенных элементах цепи изменения силы тока происходят практически одновременно, так как электромагнитные взаимодействия распространяются со скоростью света. Поэтому можно считать, что колебания силы тока во всех элементах последовательной цепи происходят по закону:
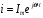
Колебания напряжения на резисторе совпадают по фазе с колебаниями силы тока
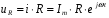 ,
,
а колебания напряжения на катушке опережают по фазе колебания силы тока на  /2.
/2.
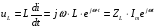 ,
,
где 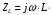 ,
,
колебания напряжения на конденсаторе отстают по фазе на  /2 от колебаний силы тока
/2 от колебаний силы тока
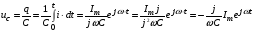 ,
,
где
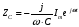 , (емкостное сопротивление)
, (емкостное сопротивление)
Поэтому уравнение можно записать так:
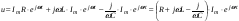
согласно закона Ома: 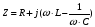 – комплексное сопротивление.
– комплексное сопротивление.
Таким образом, мы видим, что действительное число это активное сопротивление, а мнимое число – реактивное. Общее комплексное сопротивление можно найти сложением комплексных чисел, что значительно проще метода векторных диаграмм особенно для разветвленных цепей. Покажем это на примере задачи № 1.
Задача № 1.
Получить формулу, описывающую комплексное сопротивление Z двухполюсника с двумя резисторами и двумя конденсаторами.
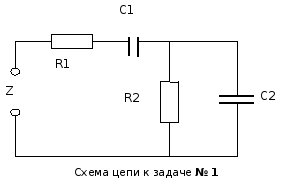
Решение:
Искомая величина Z является суммой сопротивлений Z1 и Z2 двух более простых цепей, одна из которых образована последовательным, а другая параллельным включением элементов:
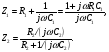
Приводя к общему знаменателя, получаем
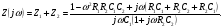
Следующую задачу решить самостоятельно.
Задача № 2.
Определить комплексное сопротивление двухполюсника, если известны R1; R2; L; C.

Задания для самостоятельного решения
Найдите действительные числа  и
и 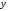 из условия равенства двух комплексных чисел: 1)
из условия равенства двух комплексных чисел: 1) 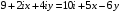 ; 2)
; 2) 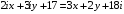 ; 3)
; 3) 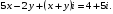
Найдите все значения аргумента комплексных чисел: 1)  ; 2)
; 2)  .
.
Представить в тригонометрической форме следующие числа: 1)  ; 2)
; 2)  .
.
Выполните деление в тригонометрической форме:
Возведите в степень: 1)  ; 2)
; 2)  .
.
Представить в показательной форме числа: 1) 1; 2)  .
.
Разложите на множители: 1)  ; 2)
; 2)  ; 3)
; 3)  .
.
Практическая работа № 2
«Построение графа по условию ситуационных задач».
Цели занятия:
1) Систематизировать и обобщить знания студентов по теории графов;
2) Выработать навыки и умения применять теорию графов в решении ситуационных задач;
3) Развивать умения пользоваться опорным конспектом и дидактическим материалом для построения графа в ходе решения задачи;
4) Воспитывать ответственное отношение к учебному труду, аккуратность в оформлении решения задачи.
Ход работы
Задача №1. Между девятью планетами солнечной системы установлено космическое сообщение. Рейсовые ракеты летают по следующим маршрутам: Земля – Меркурий; Плутон – Венера; Земля – Плутон; Плутон – Меркурий; Меркурий – Вене; Уран – Нептун; Нептун – Сатурн; Сатурн – Юпитер; Юпитер – Марс и Марс – Уран. Можно ли долететь на рейсовых ракетах с Земли до Марса?
Решение: Нарисуем схему условия: планеты изобразим точками, а маршруты ракет – линиями.
Рис. 1.
Теперь сразу видно, что долететь с Земли до Марса нельзя.
Задача № 2. Доска имеет форму двойного креста, который получается, если из квадрата 4x4 убрать угловые клетки.

Рис. 2.
Можно ли обойти ее ходом шахматного коня и вернуться на исходную клетку, побывав на всех клетках ровно по одному разу?
Решение: Занумеруем последовательно клетки доски:

Рис. 3.
А теперь с помощью рисунка покажем, что такой обход таблицы, как указано в условии, возможен:
Рис. 4.
Мы рассмотрели две непохожие задачи. Однако решения этих двух задач объединяет общая идея – представление решения с помощью графа. Заметим, что не каждая картинка такого вида будет называться графом. Например, если вас попросят нарисовать в тетради пятиугольник, то такой рисунок графом не будет.
Задача №3. В городе Маленьком 15 телефонов. Можно ли их соединить проводами так, чтобы каждый телефон был соединен ровно с пятью другими?
Решение: Допустим, что такое соединение телефонов возможно. Тогда представим себе граф, в котором вершины обозначают телефоны, а ребра – провода, их соединяющие. Подсчитаем, сколько всего получится проводов. К каждому телефону подключено ровно 5 проводов, то есть степень каждой вершины нашего графа – 5. Чтобы найти число проводов, надо просуммировать степени всех вершин графа и полученный результат разделить на 2 (т.к. каждый провод имеет два конца, то при суммировании степеней каждый провод будет взят 2 раза).
Но тогда количество проводов получится разным  . Но это число не целое. Значит наше предположение о том, что можно соединить каждый телефон ровно с пятью другими, оказалось неверным.
. Но это число не целое. Значит наше предположение о том, что можно соединить каждый телефон ровно с пятью другими, оказалось неверным.
Ответ. Соединить телефоны таким образом невозможно.
Теорема: Любой граф содержит четное число нечетных вершин.
Доказательство: Количество ребер графа равно половине суммы степеней его вершин. Так как количество ребер должно быть целым числом, то сумма степеней вершин должна быть четной. А это возможно только в том случае, если граф содержит четное число нечетных вершин.
Связность графа
Есть еще одно важное понятие, относящееся к графам – понятие связности.
Граф называется связным, если любые две его вершины можно соединить путем, то есть непрерывной последовательностью ребер. Существует целый ряд задач, решение которых основано на понятии связности графа.
Задача №4. В стране Семерка 15 городов, каждый из городов соединен дорогами не менее чем с семью другими. Докажите, что из каждого города модно добраться в любой другой.
Доказательство: Рассмотрим два произвольных А и В города и допустим, что между ними нет пути. Каждый из них соединен дорогами не менее чем с семью другими, причем нет такого города, который был бы соединен с обоими рассматриваемыми городами (в противном случае существовал бы путь из A в B). Нарисуем часть графа, соответствующую этим городам:
Рис. 5.
Теперь явно видно, что мы получили не менее различных 16 городов, что противоречит условию задачи. Значит утверждение доказано от противного.
Если принять во внимание предыдущее определение, то утверждение задачи можно переформулировать и по-другому: «Доказать, что граф дорог страны Семерка связен».
Теперь вы знаете, как выглядит связный граф. Несвязный граф имеет вид нескольких «кусков», каждый из которых – либо отдельная вершина без ребер, либо связный граф. Пример несвязного графа вы видите на рисунке:
Рис. 6.
Каждый такой отдельный кусок называется компонентой связности графа. Каждая компонента связности представляет собой связный граф и для нее выполняются все утверждения, которые мы доказали для связных графов.
Рассмотрим пример задачи, в которой используется компонента связности:
Задача №5. В Тридевятом царстве только один вид транспорта – ковер-самолет. Из столицы выходит 21 ковролиния, из города Дальний – одна, а из всех остальных городов, – по 20. Докажите, что из столицы можно долететь в город Дальний.
Доказательство: Понятно, что если нарисовать граф ковролиний Царства, то он может быть несвязным. Рассмотрим компоненту связности, которая включает в себя столицу Царства. Из столицы выходит 21 ковролиния, а из любых других городов, кроме города Дальний – по 20, поэтому, чтобы выполнялся закон о четном числе нечетных вершин необходимо, чтобы и город Дальний входил в эту же самую компоненту связности. А так как компонента связности – связный граф, то из столицы существует путь по ковролиниям до города Дальний, что и требовалось доказать.
Графы Эйлера
Вы наверняка сталкивались с задачами, в которых требуется нарисовать какую-либо фигуру, не отрывая карандаш от бумаги и проводя каждую линию только один раз. Оказывается, что такая задача не всегда разрешима, то есть существуют фигуры, которые указанным способом нарисовать нельзя. Вопрос разрешимости таких задач также входит в теорию графов. Впервые его исследовал в 1736 году великий немецкий математик Леонард Эйлер, решая задачу о Кенигсбергских мостах. Поэтому графы, которые можно нарисовать указанным способом, называются Эйлеровыми графами.
Задача №6. Можно ли нарисовать изображенный на рисунке граф не отрывая карандаш от бумаги и проводя каждое ребро ровно один раз?

Рис. 7.
Решение: Если мы будем рисовать граф так, как сказано в условии, то в каждую вершину, кроме начальной и конечной, мы войдем столько же раз, сколько выйдем из нее. То есть все вершины графа, кроме двух должны быть четными. В нашем же графе имеется три нечетные вершины, поэтому его нельзя нарисовать указанным в условии способом.
Сейчас мы доказали теорему об Эйлеровых графах:
Теорема: Эйлеров граф должен иметь не более двух нечетных вершин.
Задания для самостоятельного решения
2.1. В стране Цифра есть 9 городов с названиями 1, 2, 3, 4, 5, 6, 7, 8, 9. Путешественник обнаружил, что два города соединены авиалинией в том и только в том случае, если двузначное число, образованное названиями городов, делится на 3. Можно ли долететь по воздуху из города 1 в город 9?
2.2. В государстве 100 городов, из каждого города выходит 4 дороги. Сколько всего дорог в государстве?
2.3. В классе 30 человек. Может ли быть так, что 9 человек имеют по 3 друга, 11 – по 4 друга, а 10 – по 5 друзей?
2.4. У короля 19 вассалов. Может ли оказаться так, что у каждого вассала 1, 5 или 9 соседей?
2.5. Может ли в государстве, в котором из каждого города выходит ровно 3 дороги, быть ровно 100 дорог?
2.6. Докажите, что число людей, живших когда-либо на Земле и сделавших нечетное число рукопожатий, четно.
Практическая работа № 3
«Применение обыкновенных дифференциальных уравнений при решении прикладных задач».
Цели занятия:
1) Систематизировать и обобщить знания студентов по решению дифференциальных уравнений;
2) Выработать навыки и умения применять теоретические знания в области дифференциальных уравнений при решении прикладных задач;
3) Развивать умения пользоваться теоретическим материалом для постановки задачи и её выполнения в ходе решения;
4) Воспитывать ответственное отношение к учебному труду, настойчивости для достижения конечных результатов.
Ход работы
Пример 1: Найти закон движения тела по оси  , если оно начало двигаться из точки
, если оно начало двигаться из точки  со скоростью
со скоростью 
Решение: При прямолинейном движении скорость есть производная от пути по времени. Обозначив путь через  , имеем
, имеем  тогда
тогда  или
или  . Проинтегрировав, получим
. Проинтегрировав, получим  Так как
Так как  при
при  , то, подставив эти значения в общее решение, находим
, то, подставив эти значения в общее решение, находим  . Итак, закон движения тела имеет вид
. Итак, закон движения тела имеет вид  .
.
Пример 2: Составить уравнение кривой, проходящей через точку  и имеющей касательную с угловым коэффициентом
и имеющей касательную с угловым коэффициентом  .
.
Решение: Согласно условию, имеем
 или
или  .
.
Проинтегрировав, получим  Используя начальные условия
Используя начальные условия  и
и  , находим
, находим  . Следовательно, искомое уравнение имеет вид
. Следовательно, искомое уравнение имеет вид 
Пример 3: Вращающийся в жидкости диск замедляет свою угловую скорость за счет трения, причем сила трения пропорциональна угловой скорости. Найти: 1) скорость вращения диска в момент  с, если при
с, если при  он вращался со скоростью
он вращался со скоростью  , а при
, а при  с его скорость стала
с его скорость стала  ; 2) момент времени, когда скорость вращения диска окажется равной
; 2) момент времени, когда скорость вращения диска окажется равной  .
.
Решение: Пусть  угловая скорость вращения диска в момент времени
угловая скорость вращения диска в момент времени  тогда замедления вращения диска под воздействием силы трения равно
тогда замедления вращения диска под воздействием силы трения равно 
Согласно условию,  где
где  коэффициент пропорциональности. Разделив переменные и интегрируя, получим
коэффициент пропорциональности. Разделив переменные и интегрируя, получим


откуда или
или
 (1)
(1)
Найдем постоянную величину  при начальных условиях
при начальных условиях  при
при  . Подставив эти значения в равенство (1), имеем
. Подставив эти значения в равенство (1), имеем  , т.е.
, т.е.  . Таким образом,
. Таким образом,
 (2)
(2)
Найдем числовое значение k по следующим данным:  с и
с и  . Подставим эти значения в равенство (2):
. Подставим эти значения в равенство (2):




Подставив значение  в равенство (2), получим
в равенство (2), получим
 (3)
(3)
Найдем скорость вращения диска в момент времени  с. Подставим в равенство (3) значение
с. Подставим в равенство (3) значение  :
:
Определяем, в какой момент времени диск будет вращаться со скоростью  . Подставив в соотношение (3) значение
. Подставив в соотношение (3) значение  , имеем
, имеем

Задания для самостоятельного решения
3.1. Найти закон движения тела по оси  , если оно начало двигаться из точки
, если оно начало двигаться из точки  со скоростью
со скоростью 
3.2. Составить уравнение кривой, проходящей через точку  и имеющей касательную с угловым коэффициентом
и имеющей касательную с угловым коэффициентом  .
.
3.3. Составить уравнение кривой, проходящей через точку  , для которой отрезок касательной между точкой касания и осью абсцисс делится пополам в точке пересечения с осью
, для которой отрезок касательной между точкой касания и осью абсцисс делится пополам в точке пересечения с осью  .
.
3.4. Температура воздуха равна  . Тело охлаждается за 40 мин. от 80
. Тело охлаждается за 40 мин. от 80 до
до  . Какую температуру будет иметь тело через 30 минут после первоначального измерения?
. Какую температуру будет иметь тело через 30 минут после первоначального измерения?
3.5. Радий распадается со скоростью, пропорциональной начальному его количеству. Через сколько лет распадется половина начального его количества? Принять  (единица измерения времени – год).
(единица измерения времени – год).
3.6. Замедляющее действие трения на диск, вращающийся в жидкости, пропорционально угловой скорости. В какой момент времени скорость вращения диска окажется равной  , если при
, если при  он вращается со скоростью
он вращается со скоростью  , а при
, а при  с – со скоростью
с – со скоростью  ?
?
Практическая работа № 4
«Решение задач с применением числовых рядов».
Цели занятия:
1) Систематизировать и обобщить знания студентами числовых рядов;
2) Выработать навыки и умения применять теорию рядов в ходе решения практических задач различной сложности;
3) Развивать умения пользоваться дидактическим материалом для постановки задачи и её выполнения в ходе решения, грамотно оформлять решение задачи;
4) Формирование умения рационально, аккуратно оформлять задание на доске и в тетради.
Ход работы
Задача № 1: Найдите первые пять членов ряда  по его заданному общему члену.
по его заданному общему члену.
Решение:
Задача № 2: Найти сумму членов ряда  .
.
Решение: Находим частичные суммы членов ряда:
 ;
; 

 .
.
Запишем последовательность частичных сумм:  .
.
Общий член этой последовательности есть  . Следовательно,
. Следовательно,
 Итак, ряд сходится и его сумма равна
Итак, ряд сходится и его сумма равна  .
.
Задача № 3: Найти сумму членов ряда 
Решение: Члены данного ряда образуют геометрическую прогрессию, знаменатель которой  . Тогда п-й частичной суммой будет сумма п первых членов этой прогрессии.
. Тогда п-й частичной суммой будет сумма п первых членов этой прогрессии.

По определению суммы ряда: 

Задача № 4: Исследовать ряд на сходимость, применяя признак Даламбера:
 .
.
Решение: Преобразуем выражение  :
:
Ряд сходится по признаку Даламбера.
Задача № 5: Дан ряд . Исследовать его сходимость в точках  ,
,  ,
,  .
.
Решение: При  данный ряд превращается в числовой ряд
данный ряд превращается в числовой ряд
 .
.
Исследуем сходимость этого ряда по признаку Даламбера. Имеем
 ;
; 
то есть ряд сходится.
При  получим ряд
получим ряд
 или
или  ,
,
который расходится, так как не выполняется необходимый признак сходимости ряда.
При  получим
получим
 .
.
Это знакочередующийся ряд, который согласно признаку Лейбница, сходится.
Задача № 6: Найти промежуток сходимости степенного ряда: 
Решение:  ;
;  ;
;


Следовательно, промежуток сходимости есть  , то есть данный ряд сходится на всей числовой оси.
, то есть данный ряд сходится на всей числовой оси.
Задания для самостоятельного решения
4.1. Найдите первые пять членов ряда по его заданному общему члену:
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
4.2. Найдите п-й член ряда по его данным первым членам:
1)  2)
2)  3)
3) 
4.3. Исследовать ряд на сходимость:
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ; 5)
; 5)  .
.
4.4. Определить радиус сходимости ряда:
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
4.5. Найти промежуток сходимости степенного ряда: 
Практическая работа № 5
«Решение прикладных задач с использованием комбинаторики».
Цели занятия:
1) Обобщить понятие комбинаторной задачи, видов соединений;
2) Отработать умение решать задачи на применение формул перестановок, размещений, сочетаний;
3) Развивать умение обобщать, систематизировать на основе сравнения, делать вывод;
4) Воспитание коммуникативной и информационной культуры студентов.
Ход работы
Задача № 1: Сколькими способами могут быть расставлены 8 участниц финального забега на 8 беговых дорожках?
Решение: Число способов равно числу перестановок из 8 элементов. По формуле числа перестановок находим, что
 .
.
Задача № 2: Учащиеся второго класса изучают 8 предметов. Сколькими способами можно составить расписание на один день, чтобы в нем было 4 различных предмета?
Решение: Любое расписание на один день, составленное из 4 различных предметов, отличается от другого либо предметами, либо порядком следования предметов. Значит, в этом примере идет о размещениях из 8 элементов по 4.
.
Задача № 3: Из 15 членов туристической группы надо выбрать трех дежурных. Сколькими способами можно сделать этот выбор?
Решение: Каждый выбор отличается от другого хотя бы одним дежурным. Значит, здесь речь идет о сочетаниях из 15 элементов по 3.
Имеем:
.
Задача № 4: Из вазы с фруктами, в которой лежит 9 яблок и 6 груш, надо выбрать 3 яблока и 2 груши. Сколькими способами можно сделать такой выбор?
Решение: Выбрать 3 яблока из 9 можно  способами, а выбрать 2 груши из 6 можно
способами, а выбрать 2 груши из 6 можно  способами. Так как при каждом выборе яблок груши можно выбрать
способами. Так как при каждом выборе яблок груши можно выбрать  способами, то сделать выбор фруктов, о котором говорится в задаче, можно
способами, то сделать выбор фруктов, о котором говорится в задаче, можно 
 способами.
способами.
Имеем:
.
Задания для самостоятельного решения
5.1. Сколькими способами могут быть расставлены 5 участниц финального забега на 5-ти беговых дорожках?
5.2. Сколькими способами четверо юношей могут пригласить четырех из шести девушек на танец?
5.3. Сколькими способами из 10 человек можно выбрать комиссию, состоящую из 5 человек?
5.4. В 9 классе учатся 8 учащихся, в 10 – 6 учащихся, а в 11 – 5 учащихся. Для работы на пришкольном участке надо выделить двух учащихся из 9 класса, трех – из 10, и одного – из 11 . Сколько существует способов выбора учащихся для работы на пришкольном участке?
5.5. Семь мальчиков, в число которых входят Олег и Игорь, становятся в ряд. Найдите число возможных комбинаций, если: а) Олег должен находиться в конце ряда; б) Олег должен находиться в начале ряда, а Игорь – в конце ряда; в) Олег и Игорь должны находиться рядом.
5.6. Вычислить  ,
,  ,
,  .
.
5.7. Сократить дробь  .
.
5.8. Сколько существует перестановок букв слова «пирамида», в которых буквы п, и, р стоят рядом?
5.9. Сколько существует семизначных телефонных номеров, в которых все цифры различные и первая цифра отлична от нуля?
5.10. Сколькими способами можно расставить на полке 12 книг, из которых 5 книг – это сборники стихов, так, чтобы сборники стихов стояли рядом в произвольном порядке?
5.11. Имеется девять различных книг, четыре из которых – учебники. Сколькими способами можно расставить эти книги на полке так, чтобы все учебники стояли рядом?
5.12. В соревнованиях по футболу участвовало 12 команд. Каждая команда провела с каждой из остальных по одной игре на своем поле и по одной игре на поле соперника. Сколько всего игр было сыграно?
Практическая работа № 6
«Решение прикладных задач на нахождение вероятности события».
Цели занятия:
1) Систематизировать знания основных определений, формул теории вероятностей;
2) Выработать умения и навыки применять теоретический материал при решении вероятностных задач различного уровня;
3) Активизировать самостоятельную деятельность студентов;
4) Формирование умения аккуратно оформлять задание в тетради.
Ход работы
Задача № 1. При перевозке ящика, в котором содержались 21 стандартная и 10 нестандартных деталей, утеряна одна деталь, причем неизвестно какая. Наудачу извлеченная (после перевозки) из ящика деталь оказалась стандартной. Найти вероятность того, что была утеряна: а) стандартная деталь; б) нестандартная деталь.
Решение: а) Извлеченная стандартная деталь не могла быть утеряна; могла быть потеряна любая из остальных 30 деталей (21+10 – 1= 30), причем среди них было 20 стандартных (21 – 1 = 20). Вероятность того, что была потеряна стандартная деталь,  .
.
б) Среди 30 деталей, каждая из которых могла быть утеряна, было 10 нестандартных. Вероятность того, что потеряна нестандартная деталь,  .
.
Задача №2: Найти вероятность того, что при бросании трех игральных костей шестерка выпадет на одной (безразлично какой) кости, если на гранях двух других костей выпадут числа очков, не совпадающие между собой (и не равные шести).
Решение: Общее число элементарных исходов испытания равно числу сочетаний из шести элементов по три, то есть  .
.
Число исходов, благоприятствующих появлению шестерки на одной грани и различного числа очков (не равного шести) на гранях двух других костей, равно числу сочетаний из пяти элементов по два, то есть  .
.
Искомая вероятность равна отношению числа исходов, благоприятствующих интересующему нас событию, к общему числу возможных элементарных исходов:  .
.
Задача № 3. В билете 3 раздела. Из 40 вопросов первого раздела студент знает 30 вопросов, из 30 вопросов второго – 15, из 30 вопросов третьего – 10. Определить вероятность правильного ответа студента по билету.
Решение: Учитывая, что ответ на каждые разделы есть независимые события  и
и  , а их вероятности соответственно равны:
, а их вероятности соответственно равны:



Тогда вероятность правильного ответа на билет  , можно найти по формуле:
, можно найти по формуле:
.
Задача № 4. На склад ежедневно поступают детали с трех предприятий. С первого – 30 деталей, со второго – 20и с третьего – 40. Установлено, что 2, 4 и % продукции этих предприятий, соответственно, имеют дефекты. Найти вероятность того, что взятая наудачу деталь будет дефектна.
Решение: Обозначим:  взятая наугад деталь дефектна;
взятая наугад деталь дефектна;  деталь изготовлена на первом предприятии;
деталь изготовлена на первом предприятии;  деталь изготовлена на втором предприятии;
деталь изготовлена на втором предприятии;  деталь изготовлена на третьем предприятии. События
деталь изготовлена на третьем предприятии. События  и
и  образуют полную группу несовместных событий и
образуют полную группу несовместных событий и



Условные вероятности события  равны:
равны:



Тогда






Задача №5: Случайная величина задана законом распределения:
Найти математическое ожидание и дисперсию этой величины.
Решение:
| 
| 1 | 0 | 1 | 4 |
| 
| 0,1 | 0,3 | 0,4 | 0,2 |
Задания для самостоятельного решения
6.1. Из букв «вероятность» наугад выбирается одна буква. Какова вероятность того, что выбранная буква будет: А – согласной; В – гласной; С – буква «о».
6.2. В лотерее 1000 билетов. Из них на два билета выпадает выигрыш 200 рублей, на четыре билета – 100 рублей, на десять – по 20 рублей, на тридцать – по 10 рублей, на пятьдесят – по 5 рублей, на 200 билетов – по 1 рублю, остальные билеты без выигрыша. Какова вероятность выиграть по билету не менее 5 рублей?
6.3. На странице книги имеется 2500 букв. Буква «а» встречается 190 раз. Какова вероятность того, что случайно выбранная буква не есть буква «а»?
6.4. В магазин поступили телевизоры, 60 % которых поставило первое предприятие, 25 % – второе и 15 % – третье. Какова вероятность того, что купленный телевизор изготовлен на первом или третьем предприятии.
6.5. Из колоды в 36 карт наудачу вынимается одна. Какова вероятность того, что будет вынута пика или туз?
6.6. Вероятность попадания в мишень для первого спортсмена 0,85, а для второго – 0,8. Спортсмены независимо друг от друга сделали по одному выстрелу. Найти вероятность того, что в мишень попадет хотя бы один спортсмен.
6.7. Студент пришел на зачёт, зная из 30 вопросов только 24. Какова вероятность сдать зачет, если после отказа отвечать на вопрос преподаватель задает еще один вопрос?
6.8. Вероятность того, что в течение одного рабочего дня возникнет неполадка в определенном медицинском приборе, равна 0,05. Какова вероятность того, что не произойдет ни одной неполадки за 3 рабочих дня?
6.9. Три охотника одновременно стреляют в зайца. Шанс на успех первого охотника расценивается как 3 из 5; второго – 3 из 10; наконец, для третьего охотника они составляют лишь1 из 10. Какова вероятность того, что заяц будет подстрелен?
6.10. Случайная величина задана законом распределения:
1.
2.
| 
| 0 | 1 | 2 | 3 |
| 
| 0,5 | 0,1 | 0,2 | 0,2 |
3.
Найти математическое ожидание, дисперсию и среднее квадратичное отклонение этой величины.
Практическая работа №7
«Решение задач на нахождение приближенного значения производной функции».
Цели занятия:
1) Систематизировать и обобщить знания численного дифференцирования;
2) Отработать навыки применять теорию численного дифференцирования при решении практических задач;
3) Развивать логическое мышление, умения анализировать, выделять существенные признаки математического понятия, сравнивать и обобщать, самостоятельно выполняя задания;
4) Воспитывать аккуратность, добросовестное отношение к работе, умение работать самостоятельно.
Ход работы
Пример 1: Построить таблицу конечных разностей функции  , заданной таблично:
, заданной таблично:
| 
| 0 | 1 | 2 |
| 
| 1 | 5 | 15 |
Вычислим конечные разности первого порядка:
 ,
,
 .
.
Полученные значения разностей первого порядка занесем в столбец  таблицы разностей.
таблицы разностей.
Вычислим конечные разности второго порядка:
 .
.
Полученные значения разностей второго порядка занесем в столбец  таблицы разностей.
таблицы разностей.
Таким образом, таблица разностей для заданной функции имеет вид:
| 
| 
| 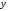
| 
| 
|
| 0 | 0 | 1 | 4 | 6 |
| 1 | 1 | 5 | 10 |
|
| 2 | 2 | 15 |
|
|
Пример 2: По таблице значений функции
| 
| 3 | 4 | 5 |
| 
| 0 | 5 | 9 |
составлена таблица конечных разностей производной функции
Вычислить приближенное значение производной функции в точке  .
.
Решение: 

=  .
.
Задания для самостоятельного решения
7.1. По таблице значений функции
| 
| 2 | 3 | 4 |
| 
| 2 | 10 | 12 |
составить таблицу конечных разностей производной функции и вычислить приближенное значение производной функции в точке  .
.
7.2. По таблице значений функции
| 
| 5 | 6 | 7 |
| 
| 11 | 9 | 15 |
составить таблицу конечных разностей производной функции и вычислить приближенное значение производной функции в точке  .
.
7.3. По таблице значений функции
| 
| 0 | 1 | 2 |
| 
| 5 | 9 | 11 |
составить таблицу конечных разностей производной функции и вычислить приближенное значение производной функции в точке  .
.
7.4. По таблице значений функции
| 
| 6 | 7 | 8 |
| 
| 9 | 13 | 20 |
составить таблицу конечных разностей производной функции и вычислить приближенное значение производной функции в точке  .
.
Практическая работа № 8
«Метод Эйлера для решения обыкновенных дифференциальных уравнений».
Цели занятия:
1) Систематизировать и обобщить знания численного решения обыкновенных дифференциальных уравнений;
2) Отработать навыки применять метод Эйлера при решении практических задач;
3) Развивать логическое мышление, умения анализировать, выделять существенные признаки математического понятия, сравнивать и обобщать, самостоятельно выполняя задания;
4) Воспитывать аккуратность, добросовестное отношение к работе, умение работать самостоятельно.
Ход работы
Многие задачи науки и техники сводятся к решению обыкновенных дифференциальных уравнений (ОДУ). ОДУ называются такие уравнения, которые содержат одну или несколько производных от искомой функции. В общем виде ОДУ можно записать следующим образом:
 ,
,
где x – независимая переменная,  – i-я производная от искомой функции, п – порядок уравнения.
– i-я производная от искомой функции, п – порядок уравнения.
Общее решение ОДУ n–го порядка содержит n произвольных постоянных  , то есть общее решение имеет вид
, то есть общее решение имеет вид  .
.
Для выделения единственного решения необходимо задать n дополнительных условий. В зависимости от способа задания дополнительных условий существуют два различных типа задач: задача Коши и краевая задача. Если дополнительные условия задаются в одной точке, то такая задача называется задачей Коши. Дополнительные условия в задаче Коши называются начальными условиями. Если же дополнительные условия задаются в более чем одной точке, т.е. при различных значениях независимой переменной, то такая задача называется краевой. Сами дополнительные условия называются краевыми или граничными.
Ясно, что при n=1 можно говорить только о задачи Коши.
Примеры постановки задачи Коши:
 ,
, 
 ,
,  ,
, 
Численные методы решения задачи Коши для ОДУ первого порядка
Постановка задачи. Найти решение ОДУ первого порядка 
на отрезке  при условии
при условии  .
.
При нахождении приближенного решения будем считать, что вычисления проводятся с расчетным шагом  , расчетными узлами служат точки
, расчетными узлами служат точки 
 промежутка
промежутка  .
.
Целью является построение таблицы
| xi | x0 | x1 | … | xn |
| yi | y0 | y1 | … | yn |
то есть находятся приближенные значения y в узлах сетки.
Интегрируя уравнение на отрезке  , получим
, получим  .
.
Вполне естественным (но не единственным) путем получения численного решения является замена в нем интеграла какой–либо квадратурной формулой численного интегрирования. Если воспользоваться простейшей формулой левых прямоугольников первого порядка
 ,
,
то получим явную формулу Эйлера:

 ,
,  .
.
Порядок расчетов:
Зная  , находим
, находим 
 , затем
, затем  и т.д.
и т.д.
Геометрическая интерпретация метода Эйлера:
Пользуясь тем, что в точке  известно решение
известно решение  и значение его производной
и значение его производной  , можно записать уравнение касательной к графику искомой функции
, можно записать уравнение касательной к графику искомой функции  в точке
в точке  :
:  (рис.1).
(рис.1).
При достаточно малом шаге h ордината 
Рис. 1.
этой касательной, полученная подстановкой в правую часть значения должна мало отличаться от ординаты
должна мало отличаться от ординаты  решения
решения задачи Коши.
задачи Коши.
Следовательно, точка  пересечения касательной с прямой
пересечения касательной с прямой  может быть приближенно принята за новую начальную точку. Через эту точку снова проведем прямую
может быть приближенно принята за новую начальную точку. Через эту точку снова проведем прямую  , которая приближенно отражает поведение касательной к
, которая приближенно отражает поведение касательной к  в точке
в точке  . Подставляя сюда
. Подставляя сюда (т.е. пересечение с прямой
(т.е. пересечение с прямой  ), получим приближенное значение
), получим приближенное значение в точке
в точке  :
:  и т.д. В итоге для i–й точки получим формулу Эйлера.
и т.д. В итоге для i–й точки получим формулу Эйлера.
Пример 1: Найти методом Эйлера численное решение дифференциального уравнения  при начальных условиях
при начальных условиях  , принимая
, принимая  . Ограничиться отысканием первых пяти значений.
. Ограничиться отысканием первых пяти значений.
Решение: 
Задания для самостоятельного решения
8.1. Найти методом Эйлера численное решение дифференциального уравнения  при начальных условиях
при начальных условиях  на отрезке
на отрезке  , принимая
, принимая  .
.
8.2. Найти методом Эйлера численное решение дифференциального уравнения  при начальных условиях
при начальных условиях  на отрезке
на отрезке  , принимая
, принимая  .
.
8.3. Найти методом Эйлера численное решение дифференциального уравнения  при начальных условиях
при начальных условиях  на отрезке
на отрезке  , принимая
, принимая  .
.
8.4. Найти методом Эйлера численное решение дифференциального уравнения  при начальных условиях
при начальных условиях  на отрезке
на отрезке  , принимая
, принимая  .
.
8.5. Найти методом Эйлера численное решение дифференциального уравнения  при начальных условиях
при начальных условиях  на отрезке
на отрезке  , принимая
, принимая  .
.








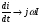

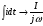

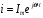
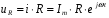 ,
,  /2.
/2. 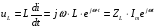 ,
, 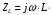 ,
, 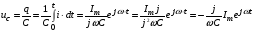 ,
, 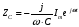 , (емкостное сопротивление)
, (емкостное сопротивление)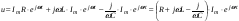
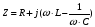 – комплексное сопротивление.
– комплексное сопротивление.
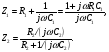
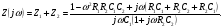

 и
и 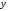 из условия равенства двух комплексных чисел: 1)
из условия равенства двух комплексных чисел: 1) 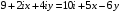 ; 2)
; 2) 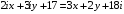 ; 3)
; 3)