Практическое занятие № 3 "Выделение связных компонентов орграфа"

ИНСТРУКЦИОННАЯ КАРТА

на выполнение практического занятия № 3

по МДК.01.02 Математический аппарат для построения компьютерных сетей (тема 1. Теория графов)

Тема занятия: Выделение связных компонентов орграфа.

Цель проведения занятия: научиться определять компоненты сильной связности в орграфе; закрепить навыки моделирования графов в графической среде Grafoanalizator1.3.3 rus.

После выполнения работы студент должен

знать: основные понятия теории графов, матричное представление графов, связность графов;

уметь: определять компоненты сильной связности в орграфе.

Материально-техническое оснащение рабочего места: инструкционные карты, конспект.

Инструктаж по технике безопасности

Рекомендованная литература:

1. Спирина М.С., Дискретная математика: Учебник для студ. Учреждений сред. проф. образования / М.С.Спирина, П.А.Спирин. –М.: Издательский центр «Академия», 2004. –368 с.

2. Александров А. В. и др. Прикладные алгоритмы на графах. Учебное пособие, ВлГУ, 2005

3. Харари Фрэнк. Теория графов / Харари Фрэнк ; Пер. с англ. В.П.Козырева; Под ред. Г.П.Гаврилова. - 4-е изд. - М. : URSS : Либроком, 2009. - 296 с

4. Битюцкий В. П. Электронный учебник: Дискретная математика / http://ait.ustu.ru/uploaded/materialy-po-disciplinam/discret-mathematics/el_ucheb/index.htm

5. Справочные данные по математике: Элементы теории графов. [Электронный ресурс]. – Режим доступа: http://book.itep.ru/10/grap1021.htm, свободный. – Загл. с экрана.

Содержание и порядок выполнения задания

Задание 1. Выделить компоненты связности ориентированного графа, изображенного на рисунке.

а) 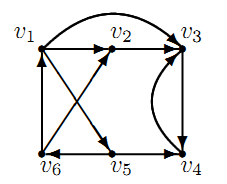б)

Задание 2 (индивидуальное). Выделить компоненты сильной связности для графа из практической работы №2 (задание 3). Проверить решение в программе Grafoanalizator1.3.3 rus.

Вопросы для самоконтроля:

1. Какой граф называется связным?

2. Какой граф называется несвязным?

3. Что называется компонентой связности графа?

Краткие сведения по теоретической части работы В теории графов, понятие связности графа является ключевым при решении многих прикладных задач. Граф G(V,E) называется связным, если все его вершины связаны между собой, т.е. взаимно достижимы. Если для графа G(V,E) можно указать пару несвязных вершин, то граф называется несвязным. Пример несвязного и связного графов.

Компонента связности графа — некоторое множество вершин графа такое, что для любых двух вершин из этого множества существует путь из одной в другую, и не существует пути из вершины этого множества в вершину не из этого множества. Для ориентированных графов определено понятие сильной компоненты связности. Пример компонент связности графа G=(V,E): V1 = {v1, v2, v5, v6} и V2 = {v3, v4, v7, v8}.

Свойства компонент связности.
1. Каждая вершина графа входит лишь в одну компоненту связности.
2. Любой конечный граф имеет конечное число компонент связности.
3. Граф, состоящий из единственной компоненты связности, является связным.
4. Каждая компонента связности графа является его подграфом.
Теорема. Если в конечном графе G ровно две вершины u и v имеют нечетную степень, то они связаны.

Алгоритм определения сильной связности орграфа:

1. Построить множества достижимости и контрдостижимости или матрицы достижимости и контрдостижимости для оргарфа

2. Выбрать некоторую вершину v_i

3. Найти множество VS_i =R(v_i)∩Q(v_i). Вершинно-порожденный на множестве вершин VS_i подграф графа G представляет сильную компоненту

4. Если множество V- VS_i пусто, то все сильные компоненты найдены, в противном случае строится вершинно-порожденный на V-VS_i подграф и перейти к пункту 2.

Методические рекомендации по выполнению и оформлению

Порядок выполнения работы:

1. Изучить инструкцию к практической работе.

2. Выполнить задания.

3. Оформить отчет.

Содержание отчета о занятии:

1. Тема.

2. Цель.

4. Практическое задание.

5. Ответ на 1 контрольный вопрос (по варианту).

Инструкционная карта составлена преподавателем: Шнаревой Г.В.