Практикум по теме "Системы счисления и перевод между ними. ЕГЭ -2020, задание 1."

ЕГЭ – 1. Системы счисления и двоичное представление информации

в памяти компьютера (базовый уровень, примерное время

решения – 1 минута). Теория по теме – здесь.

Рассмотрим различные задачи, которые встречаются в данном задании, и способы их решения. Начнем с самых простых задач, которые вряд ли будут на ЕГЭ, но решение которых позволит нам быстро и просто решать самые сложные, и придем к самым сложным.

Задача 1. Как представлено число 73₁₀ в двоичной системе счисления?

a) 1001011₂ b) 111101₂ c) 101011₂ d) 1001001₂

Решение. Для быстрого и точного решения задачи достаточно разложить исходное число на сумму степеней двойки, а затем записать «1» на место существующей степени и «0» - на место пропущенной степени двойки.

Тогда 73₁₀ = 2⁶ + 2³ + 2⁰ = 1001001₂

(шестая степень есть – 1, пятой нет – 0, четвертой нет – 0, третья есть – 1, второй нет – 0, первой нет – 0, нулевая есть – 1).

Возможные ловушки:

• если исходное число четное, то нужно не забыть о нулевой степени числа.

• вариант ответа b). Нужно помнить правильность перевода числа из десятичной системы счисления в двоичную, что десятичная система не «дружит» ни с какой другой в окружении систем с основанием, меньшим 100 (а на другие задачи мы не решаем), и пользоваться таблицей «дружбы» для перевода в двоичную систему счисления нельзя.

Проверка решения: По закономерности 4 из теоретической части:  N^L-1 ≤  Ch ^L.

Тогда 64 ≤ 73 ⁶ ≤ 73 ⁷

Длина результата равна 7, как и в полученном ответе.

Эта проверка действует на оба варианта из возможных совершенных ошибок.

На ЕГЭ более вариантов ответов не предусматривается.

Ответ: d (1001001)

Задача 2. Сколько единиц в двоичной записи числа 187 ?

Решение. Для быстрого и точного решения задачи достаточно разложить исходное число на сумму степеней двойки, а затем посчитать количество присутствующих степеней.

Тогда 187 = 128 + 32 + 16 + 8 + 2 + 1 , то есть будет всего шесть степеней двойки.

Заметим, что более никаких действий для получения ответа здесь выполнять не нужно!

Для проверки правильности решения достаточно сложить полученные числа и сравнить их с исходным числом.

Ответ: 6

Задача 3. Сколько нулей в двоичной записи числа 204 ?

Решение. Для быстрого и точного решения задачи достаточно разложить исходное число на сумму степеней двойки, а затем посчитать количество присутствующих степеней.

Тогда 205 = 128 + 64 + 8 + 4 , то есть будет всего 4 степени двойки. А длина числа при переводе в двоичную систему счисления будет равна 8 (2⁷ ≤ 205 ⁸). Тогда количество нулей в числе будет рано разнице между ними: 8 - 4 = 4.

Заметим, что более никаких действий для получения ответа здесь выполнять не нужно!

Ответ: 4

Задача 4. Как записывается число A95₁₆ в восьмеричной системе счисления?

Решение. Шестнадцатеричная и восьмеричная системы счисления являются «дружественными» («родственными») системами, поэтому для решения задания достаточно использовать таблицу «дружбы» и принцип перевода чисел с ее помощью (см. теорию по теме).

Тогда A95₁₆ = 1010 1001 0101₂ = 101 010 010 101₂ = 5225₈.

Ответ: 5225

Задача 5. Дано: а = 9C₁₆, b = 236₈. Какое из чисел С, записанных в двоичной системе счисления, удовлетворяет неравенству ?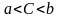

a) 10011010₂ b) 10011110₂ c) 10011101₂ d) 11011110₂

Решение. Заметим главное: исходные числа даны здесь в различных системах счисления. Для решения задачи нужно сначала привести их в одну – любую, удобную Вам для вычислений, а затем выполнять дальнейшие действия.

Здесь числа даны в дружественных восьмеричной, шестнадцатеричной и двоичной системах, поэтому удобнее всего перевести первое число и ответы в восьмеричную систему и найти подходящий вариант решения.

Тогда 9C₁₆ = 1001 1100₂ = 10 011 100₂ = 234₈;

a) 10011010₂ = 10 011 010₂ = 232₈;

b) 10011110₂ = 10 011 110₂ = 236₈;

c) 10011101₂ = 10 011 101₂ = 235₈;

d) 11011110₂ = 11 011 110₂ = 336₈.

Правильный ответ – с), но рекомендуется не останавливаться, а проверить все варианты ответов, чтобы быть уверенным в правильном решении.

Ответ: с

Задача 6. Даны 4 целых числа, записанные в двоичной системе:

10111010, 10110100, 10101111, 10101100.
Сколько среди них чисел, меньших, чем 9C₁₆ + 37₈?

Решение. Заметим главное: исходные числа даны здесь в различных системах счисления. Для решения задачи нужно сначала привести их в одну – любую, удобную Вам для вычислений, а затем выполнять дальнейшие действия.

Здесь числа даны в дружественных восьмеричной, шестнадцатеричной и двоичной системах, поэтому удобнее всего перевести первое число и ответы в восьмеричную систему и найти подходящий вариант решения.

Тогда 9C₁₆ = 1001 1100₂ = 10 011 100₂ =234₈;

234₈ + 37₈ = 273₈;

10111010₂ = 272₈ (подходит);

10110100₂ = 264₈ (подходит);

10111111₂ = 277₈ (не подходит);

10101100₂ = 259₈ (подходит).

Ответ: 3

Задача 7. Укажите наибольшее четырёхзначное шестнадцатеричное число, двоичная запись которого содержит ровно 5 значащих нулей. В ответе запишите только само шестнадцатеричное число, основание системы счисления указывать не нужно.

Решение. Наибольшее четырехзначное шестнадцатеричное число равно FFFF. Чтобы число с пятью значащими нулями оставалось наибольшим, нули должны стоять в конце числа, тогда переводим две последние цифры в двоичную систему счисления, заменяем там последние пять цифр на нули и переводим обратно в шестнадцатеричную систему, получаем:

FF₁₆ = 11111111₂ = 11100000₂ = E0₁₆

Ответ: FFE0

Задача 8. (А.Н. Носкин) Задан отрезок [a, b]. Число a – наименьшее число, восьмеричная запись которого содержит ровно 3 символа, один из которых – 3. Число b – наименьшее число, шестнадцатеричная запись которого содержит ровно 3 символа, один из которых – F. Определите количество натуральных чисел на этом отрезке (включая его концы).

Решение.

a = 103₈; b = 10F₁₆ = 1 0000 1111₂ = 417₈

417₈ – 103₈ + 1 = 315₈ = 205 (плюс 1, потому что в разность входит только один конец отрезка, добавляем второй).

Ответ: 205

Задача 9. (Е.В. Куцырь) Определите количество натуральных чисел, кратных основанию четверичной системы счисления и удовлетворяющих неравенству: 734₈  x ₁₆

Решение.

1E4₁₆ = 1 1110 0100₂ = 744₈

744₈ – 734₈ = 10₈ = 8 – всего в интервале, включая исходное число. Тогда чисел, кратных 4, в интервале ровно 2.

Ответ: 2
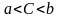