© 2020 1589 0


СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 17.05.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

Правила диференціювання: похідна суми; добутку і частки функцій. Рівняння дотичної до графіка функції
Категория:
Математика
19.03.2020 16:20


 u(x))’ = cu’(x), (с – стала, тобто число)
u(x))’ = cu’(x), (с – стала, тобто число)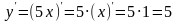 .
.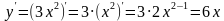 .
.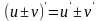
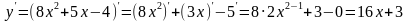 .
.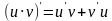
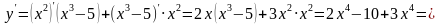
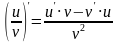
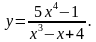
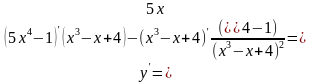
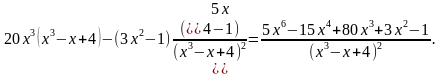
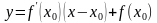
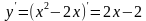 ;
;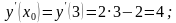
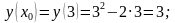
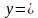
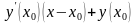 - рівняння дотичної
- рівняння дотичної


















