Презентация "Дифференцированные платежи", задание № 16 ЕГЭ по математике, профильный уровень

Задание № 16 ЕГЭ по математике, профильный уровень. Дифференцированные платежи

Повышающий и понижающий коэффициент

Если S увеличивается на k%, то

Пример: S увеличивается на 3%, тогда

Если S уменьшается на k%, то

Пример: S уменьшается на 13%, тогда

Задача1.  Цена товара была снижена сначала на 24%, а затем на 50% от новой цены. Найти общий процент снижения цены товара.

Решение.  

Пусть цена товара = S. После первого снижения цены получилось = 0,76 S . Дальше эту стоимость уменьшают еще на 50%, т.е. =.

Т.е. от первоначальной цены осталось 38% , а это значит, что цена была снижена на 62% .

Ответ.   Общий процент снижения равен 62%.

Задача2. Цена изделия сначала возросла на 20%, а потом на столько же процентов была снижена. Как и на сколько процентов изменилась цена по сравнению с первоначальной?

Решение: Пусть цена товара = S. После увеличения цены на 20%, товар стал стоить

Таким образом стоимость товара снизилась на 4%. Ответ: Цена снизилась на 4%.

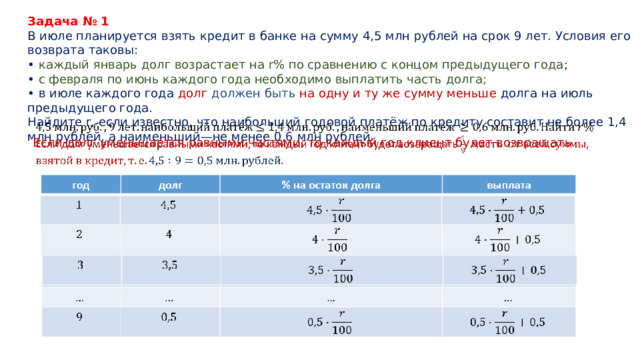
Задача № 1

В июле планируется взять кредит в банке на сумму 4,5 млн рублей на срок 9 лет. Условия его возврата таковы:

• каждый январь долг возрастает на r% по сравнению с концом предыдущего года ;

• с февраля по июнь каждого года необходимо выплатить часть долга;

• в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.

Найдите r, если известно, что наибольший годовой платёж по кредиту составит не более 1,4 млн рублей, а наименьший—не менее 0,6 млн рублей.

Если долг уменьшается равными частями, то каждый год клиент будет возвращать

год

год

долг

долг

% на остаток долга

% на остаток долга

выплата

выплата

…

…

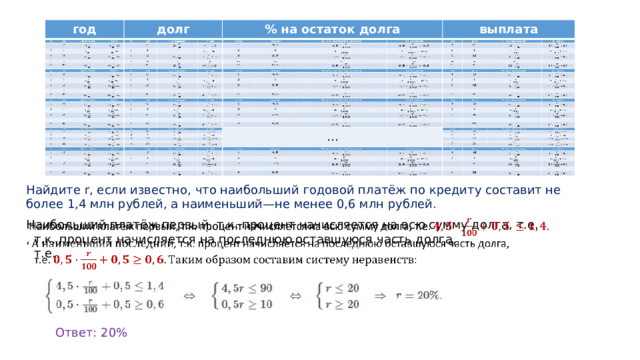
Найдите r, если известно, что наибольший годовой платёж по кредиту составит не более 1,4 млн рублей, а наименьший—не менее 0,6 млн рублей.

Наибольший платёж первый, т.к. процент начисляется на всю сумму долга, т.е.

, т.к. процент начисляется на последнюю оставшуюся часть долга,

т.е.

Ответ: 20%

Задание № 2

В июле планируется взять кредит в банке на сумму 28 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:

• каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;

• с февраля по июнь каждого года необходимо выплатить часть долга;

• в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.

Чему будет равна общая сумма выплат (в млн рублей) после полного погашения кредита, если наибольший годовой платёж составит 9 млн рублей?

S = 28 млн. рублей сумма кредита сроком на n лет, где n – целое.

долг уменьшается на одну и ту же величину, т.е. на .

Следовательно, ежегодные платежи равны плюс начисленные проценты на остаток долга .

Наибольший годовой платёж первый, т.к. процент начисляется на всю сумму долга.

Таким образом:

Значит кредит взят на 14 лет. Каждый год клиент возвращает одну и ту же часть долга 28 : 14 = 2 млн. руб.

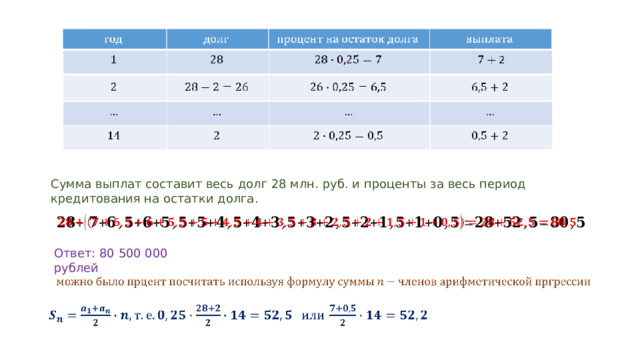
Сумма выплат составит весь долг 28 млн. руб. и проценты за весь период кредитования на остатки долга.

Ответ: 80 500 000 рублей

Задача № 3

Пётр взял кредит в банке на срок 12 месяцев. По договору Пётр должен вернуть кредит ежемесячными платежами. В конце каждого месяца к оставшейся сумме долга добавляется r% этой суммы, и своим ежемесячным платежом Пётр погашает эти добавленные проценты и уменьшает сумму долга. Ежемесячные платежи подбираются так, чтобы долг уменьшался на одну и ту же величину каждый месяц. Известно, что общая сумма, выплаченная Петром банку за весь срок кредитования, оказалась на 13% больше, чем сумма, взятая им в кредит. Найдите r.

S – кредит сроком на 12 месяцев. Сумма выплат на 13% больше суммы взятой в кредит, т.е. 1,13S.

Найти r %.

(остаток долга)

…

…

…

…

Найдём сумму выплат:

Задача № 4

В июле планируется взять кредит в банке на сумму 16 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:

• каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;

• с февраля по июнь каждого года необходимо выплатить часть долга;

• в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.

На сколько лет планируется взять кредит, если известно, что общая сумма выплат после его полного погашения составит 38 млн рублей?

кредит сроком на n лет. так как каждый год долг должен уменьшатся на одну и ту же сумму, то заемщик каждый год выплачивает проценты начисленные за год на остаток и .

Тогда остаток через год будет ,   через 2 года    и так далее.

Общая сумма выплат равна начисленным процентам плюс сам кредит

Ответ: 10 лет .

Задача № 5

15-го января планируется взять кредит в банке на сумму 2,4 млн рублей на 24 месяца. Условия его возврата таковы:

— 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.

Какую сумму нужно выплатить банку в первые 12 месяцев?

S = 2,4 млн. рублей кредит сроком на 24 месяца. Каждый месяц банк начисляет 3% на остаток долга, а заемщик выплачивает эти проценты и уменьшает сумму долга равномерно на одну и ту же величину, т.е. на =0,1 млн. руб.

12

12

…

1,3

1,3

…

…

…

…

…

…

…

За первые 12 месяцев банку будет выплачено:

Ответ: 1 866 000 рублей

Задача № 6

15-го декабря планируется взять кредит в банке на 26 месяцев. Условия возврата таковы:

— 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца с 1-го по 25-й долг должен быть на 20 тысяч рублей меньше долга на 15-е число предыдущего месяца;

— к 15-му числу 26-го месяца кредит должен быть полностью погашен.

Какой долг будет 15-го числа 25-го месяца, если общая сумма выплат после полного погашения кредита составит 1407 тысяч рублей?

S – кредит в тыс. рублей сроком на 26 месяцев.

В течение первых 25 месяцев банк начисляет 3% на остаток, а заемщик выплачивает эти проценты и еще 20 тыс. рублей. Таким образом, через 1 месяц остаток долга будет S –20, через 2 месяца S –40 и так далее, а через 25 месяцев S –500.

480

480

общая сумма платежей по условию равна 1407 тысяч рублей

Значит долг в конце 25-го месяца равен:

Ответ: 400 000 рублей

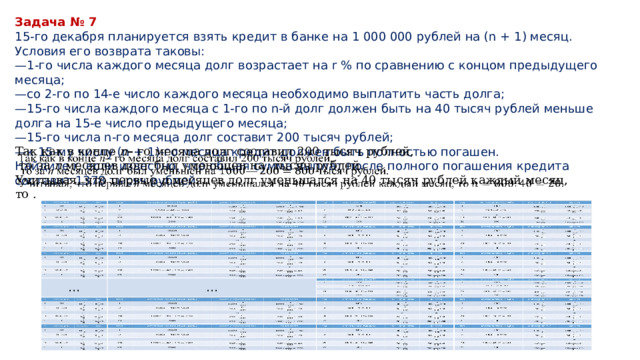
Задача № 7

15-го декабря планируется взять кредит в банке на 1 000 000 рублей на (n + 1) месяц. Условия его возврата таковы:

— 1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца;

— cо 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца с 1-го по n-й долг должен быть на 40 тысяч рублей меньше долга на 15-е число предыдущего месяца;

— 15-го числа n-го месяца долг составит 200 тысяч рублей;

— к 15-му числу (n + 1)-го месяца кредит должен быть полностью погашен.

Найдите r, если известно, что общая сумма выплат после полного погашения кредита составит 1378 тысяч рублей .

Так как в конце n – го месяца долг составил 200 тысяч рублей,

то за n месяцев долг был уменьшен на тысяч рублей.

Учитывая, что первые n месяцев долг уменьшался на 40 тысяч рублей каждый месяц, то .

(тыс. руб.)

…

…

…

…

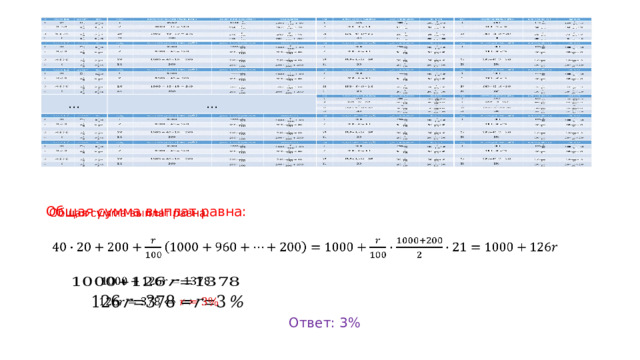
(тыс. руб.)

1000

…

…

…

…

Общая сумма выплат равна:

Ответ: 3%

Задача № 8

В июле 2023 года планируется взять кредит на 10 лет. Условия его возврата таковы:

— каждый январь с 2024 по 2028 год долг возрастает на 18% по сравнению с концом предыдущего года;

— каждый январь с 2029 по 2033 год долг возрастает на 16% по сравнению с концом предыдущего года;

— с февраля по июнь каждого года необходимо выплатить часть долга;

— в июле каждого года должен быть на одну и ту же величину меньше долга на июль предыдущего года;

— к июлю 2033 года долг должен быть полностью погашен.

Какую сумму планируется взять в кредит, если общая сумма выплат по кредиту должна составить 1470 тысяч рублей?

S – сумма кредита на 10 лет. Сумма выплат 1470 тысяч рублей.

Первые 5 лет долг возрастает на 18%.

Следующие пять лет долг возрастает на 16%.

Все десять лет долг уменьшается на одну и ту же часть .

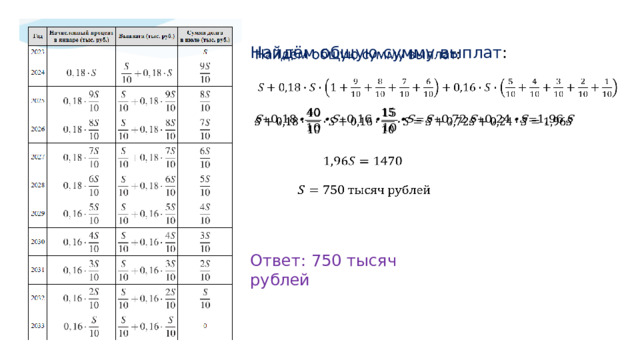
Найдём общую сумму выплат :

Ответ: 750 тысяч рублей

Задача № 9

В июле 2025 года планируется взять кредит в банке на некоторую сумму на 10 лет. Условия его возврата таковы:

— каждый январь долг увеличивается на 10% по сравнению с концом предыдущего года;

— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;

—   в июле 2026, 2027, 2028, 2029, 2030 годов долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года;

— в июле 2030 года долг должен составлять 800 тыс. руб.;

—   в июле 2031, 2032, 2033, 2034, 2035 годов долг должен быть на другую одну и ту же сумму меньше долга на июль предыдущего года;

Найдите начальную сумму кредита, если сумма выплат по кредиту равна 2090 тысяч рублей.

S – кредит.

.

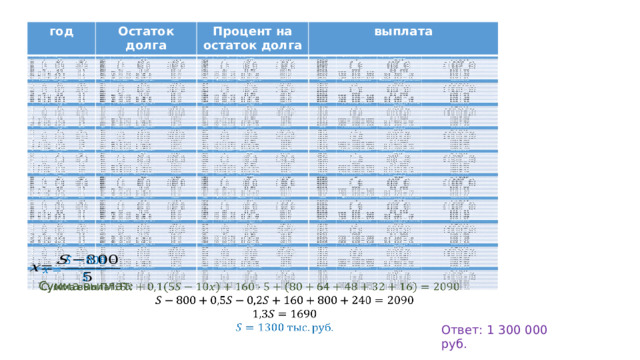
год

год

Остаток долга

Остаток долга

Процент на остаток долга

Процент на остаток долга

выплата

выплата

Сумма выплат:

Ответ: 1 300 000 руб.

Задача № 10

В июле 2025 года планируется взять кредит на десять лет в размере 1300 тыс. рублей. Условия его возврата таковы:

— каждый январь долг будет возрастать на 20 % по сравнению с концом предыдущего года;

— с февраля по июнь каждого года необходимо оплатить одним платежом часть долга;

— в июле 2026, 2027, 2028, 2029 и 2030 годов долг должен быть на какую-то одну и ту же величину меньше долга на июль предыдущего года;

— в июле 2031, 2032, 2033, 2034 и 2035 годов долг должен быть на другую одну и ту же величину меньше долга на июль предыдущего года;

— к июлю 2035 года долг должен быть выплачен полностью.

Известно, что сумма всех платежей после полного погашения кредита будет равна 2580 тыс. рублей.

Сколько рублей составит долг в июле 2030 года?

Пусть

х – выплата, на которую уменьшается долг в период с 2026 по 2030 годы ,

у – выплата на которую уменьшается долг в период с 2031 по 2035 годы .

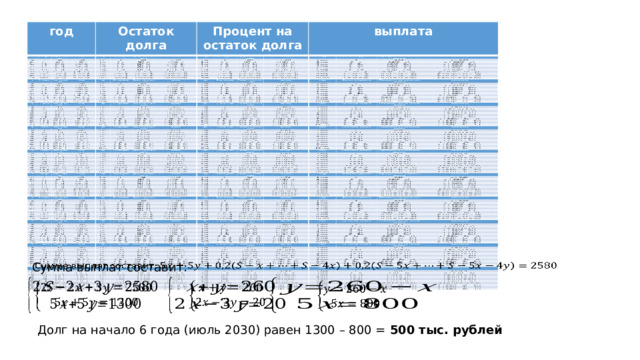
год

год

Остаток долга

Остаток долга

Процент на остаток долга

Процент на остаток долга

выплата

выплата

Сумма выплат составит:

Долг на начало 6 года (июль 2030) равен 1300 – 800 = 500 тыс. рублей

Сумма кредита 1300 тысяч рублей, значит

год

год

Долг в январе

Долг в январе

C %

C %

Долг в июле

Долг в июле

выплата

выплата

Сумма выплат равна 2580 тысяч рублей, поэтому

Необходимо было найти долг в 2030 году, т.е.

Ответ: 500 тысяч рублей

Задачи для самостоятельной работы

15 января планируется взять кредит в банке на 16 месяцев. Условия его возврата таковы:

— 1-го числа каждого месяца долг возрастает на 2 % по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.

Какую сумму следует взять в кредит, чтобы общая сумма выплат после полного погашения равнялась 2,34 млн рублей?

№ 1

№ 2

15 января планируется взять кредит в банке на 48 месяцев. Условия его возврата таковы:

• 1-го числа каждого месяца долг возрастает на r% по сравнению с концом предыдущего месяца;

• со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

• 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.

Известно, что общая сумма денег, которую нужно выплатить банку за весь срок кредитования, на 49% больше, чем сумма, взятая в кредит. Найдите r.

Задачи для самостоятельной работы

15-го декабря планируется взять кредит в банке на сумму 500 тысяч рублей на 31 месяц. Условия возврата таковы:

— 1-го числа каждого месяца долг возрастает на 1% по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца с 1-го по 30-й долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца;

— 15-го числа 30-го месяца долг составит 200 тысяч рублей;

— к 15-му числу 31-го месяца кредит должен быть полностью погашен.

Найдите общую сумму выплат после полного погашения кредита.

№ 3

15-го декабря планируется взять кредит в банке на 21 месяц. Условия возврата таковы:

№ 4

— 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца с 1-го по 20-й долг должен быть на 30 тысяч рублей меньше долга на 15-е число предыдущего месяца;

— к 15-му числу 21-го месяца кредит должен быть полностью погашен.

Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 1604 тысяч рублей?

Задачи для самостоятельной работы

№ 5