Презентація до уроку на тему: " Нескінчена спадна геометрична прогресія, | q |

Мета

сформувати поняття нескінченної геометричної прогресії ( вивести формулу для обчислення її суми; сформувати вміння застосувати цю формулу до розв’язування вправі, зокрема, для запису періодичного десяткового дробу у вигляді звичайного.

“ МОЗКОВИЙ ШТУРМ”

Правила проведення:

• не кажіть усе, що спаде вам на думку;
• не обговорюйте і не критикуйте висловлювань інших;
• можна повторювати ідеї, запропоновані іншими;
• розширення запропонованої ідеї заохочується.

1. Яка з наведених послідовностей є геометричною прогресією?

А) 2; 6; 18; 36; В) 4; 8; 16; 32;

Б) 80; 40; 20; 5; Г)2; -10; 50; 250 .

2. Яка з наведених послідовностей є геометричною прогресією?

А) 6; 18; 54; 162; В) 3; 8; 13; 18;

Б) 1; 2; 3; 5; Г) 21; 19; 17; 15.

3. Знайдіть знаменник геометричної прогресії (bn), якщо b6 = 14 / 15 і b7 =2 /3.

А) 3/7; Б) 5/7; В) 7/5; Г) 7/3.

4. Знайдіть перший член геометричної прогресії, якщо її другий член b2 =12, знаменник q = -3.

А) 4; Б) -4 ; В) 36; Г) -36.

5. Чому дорівнює п’ятий член геометричної прогресії, якщо її перший член b1 = 405, а знаменник q = -⅓?

А)-5; Б) 5 ; В)-3; Г) 3.

6. Знайти невідомий член геометричної прогресії: 3; х; 27 ; 81.

А)9; Б) 9; В)3; Г) 343.

7. Запишіть у вигляді суми розрядних одиниць числа:

• 324; 2) 32,4; 3) 0,172;

4) 0,(2); 5) 1,5(3).

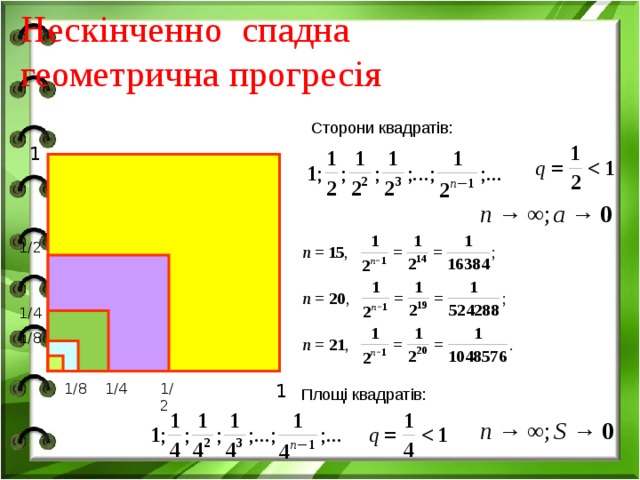
Нескінченно спадна геометрична прогресія

Сторони квадратів:

1

1/2

1/4

1/8

1/8

1/2

1/4

1

Площі квадратів:

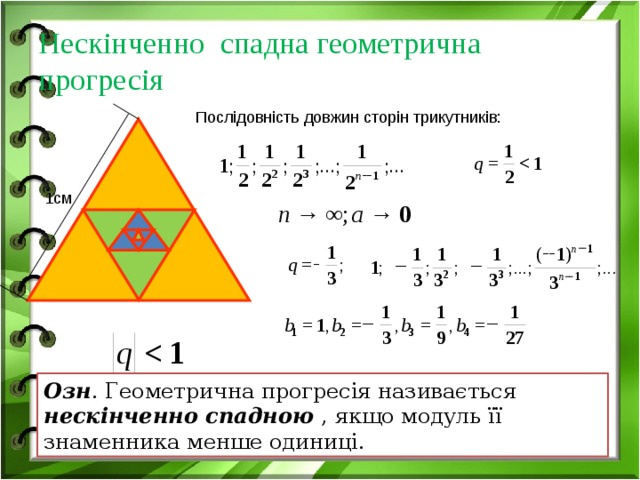
Нескінченно спадна геометрична прогресія

Послідовність довжин сторін трикутників:

1см

Озн . Геометрична прогресія називається нескінченно спадною , якщо модуль її знаменника менше одиниці.

Таким чином, сумою нескінченної спадної геометричної про­гресії називається число, до якого наближається сума п перших членів цієї прогресії, якщо п нескінченно збільшується.

Сума S нескінченної спадної геометричної про­гресії дорівнює:

S =

Задача 1 . Чому дорівнює сума нескінченної геометричної прогресії, якщо b 1 = 16, а знаменник q = 1/2 ?

Задача 2. Чому дорівнює знаменник нескінченної геометричної прогресії, перший член якої b 1 = - 15, а сума дорівнює 75?

Задача 3 . Знайдіть суму нескінченної спадної геометричної про­гресії 9; 3; 1; ... .

Задача 4. Знайдіть суму нескінченної спадної геометричної прогресії, якщо b 4 = 1/8 , q = 1/2 .

Задача 5. Знайдіть суму нескінченної геометричної прогресії (b n ), якщо b 2 - b 4 = 1,5 і b 1 - b 3 = 3.

Задача 6. Подати у вигляді звичайного дробу нескінченні періодичні десяткові дроби:

а) 0,3333… ; б) 0,(5)

в) 1,(3) г) 1,2(3) д) 5,25(7)

“ Сходинки”

Оцініть свою діяльність на уроці на сходинках знань

Все розумію,

все виходить

Розумію, але потрібно ще попрацювати

Погано розумію

новий матеріал

Домашнє завдання

§ 28 - 29, конспект

№ 828, №832, № 845,

стр.198, 202