Презентация "Элементы комбинаторики, статистики и теории вероятностей"

Элементы комбинаторики и теории вероятностей

Возникновение теории вероятностей в современном смысле слова относится к середине XVII века и связано с исследованиями Паскаля (1623-1662), Ферма (1601-1665) и Гюйгенса (1629-1695) в области теории азартных игр. В этих работах постепенно сформировались такие важные понятия, как вероятность и математическое ожидание; были установлены их основные свойства и приемы их вычисления. Наряду с задачами азартных игр  уже в самом начале возникновения  теории вероятностей появились задачи, связанные с составлением таблиц смертности и вопросами страхования. В Лондоне уже с 1592 года велись точные записи о смертности.

Б .  Паскаль

П . Ферма

Х .  Гюйгенс

Крупный шаг вперед в развитии теории вероятностей связан с работами Якова Бернулли (1654-1705). Ему принадлежит первое доказательство одного из важнейших положений теории вероятностей – так называемый закон больших чисел. Он гласит: явления, вероятностные при их малом числе, при большом количестве становятся закономерными, при очень большом – неизбежными.

Яко в Бернулли

Ночью светит солнце

1 января – праздничный день

При броске кости выпало «7»

При броске монеты выпал «орел»

При броске монеты выпала «решка»

Равновозможные события

Невозможное событие

Достоверное событие

Случайное событие

СЛУЧАЙНОЕ -

НЕВОЗМОЖНОЕ -

РАВНОВОЗМОЖНЫЕ -

ДОСТОВЕРНОЕ -

событие, которое может произойти, а может и не произойти.

событие, которое в данных условиях (опыте) не может произойти.

события, любое из которых не обладает никаким преимуществом появляться чаще при многократных испытаниях

событие, которое при данных условиях всегда произойдет

Вероятностью события А называется отношение числа благоприятных исходов для события А к числу всех равновозможных исходов.

- формула Лапласа

n - число равновозможных исходов

k - число благоприятных исходов события А

Алгоритм нахождения вероятности

1.Определить, что является элементарным событием А.

2.Найти общее число элементарных событий N .

3.Определить, какие элементарные события

благоприятствуют событию А, и найти их число N(A) .

4.Найти вероятность Р(А) события А

В случайном эксперименте симметричную монету бросают сто раз.

Найдите вероятность того, что решка выпадет при 101 бросании.

Р

В случайном эксперименте симметричную монету бросают дважды.

Найдите вероятность того, что решка выпадет ровно один раз.

ОО

РР

РО

ОР

Монету бросают трижды. Найдите вероятность того,

что первые два броска оканчиваются одинаково.

РО

ОР

РР

ОО

В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел выпадет ровно один раз

ООО

РОО

РОР

ООР

РРО

ОРО

РРР

ОРР

В случайном эксперименте симметричную монету бросают четырежды. Найдите вероятность того, что орёл не выпадет ни разу

РРРР ООРР ОООР РРОО

ООРО РРРО ОРРО ОРОО

РРОР РООР РООО РОРР

ОРОР ОРРР РОРО ОООО

Переформулируем вопрос:

найти вероятность того, что решка выпадет 4 раза

2 способ

Вероятность выпадения решки при первом броске

Т.к. бросков 4, то вероятность выпадения решки при каждом броске

На чемпионате по прыжкам в воду выступают 25 спортсменов, среди них 8 прыгунов из России и 9 прыгунов из Парагвая. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что шестым будет выступать прыгун из Парагвая

Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 бадминтонистов, среди которых 10 участвуют из России, в том числе Руслан Орлов. Найдите вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России.

Для Орлова возможны 25 партнеров, из них 9 русские

В группе иностранных туристов 51 человек, среди них 2 француза. Для посещения маленького музея группу случайным образом делят на 3 подгруппы, одинаковые по численности. Найдите вероятность того, что французы окажутся в одной подгруппе.

Будем считать, что первый француз уже занял место в какой-то подгруппе. В каждой подгруппе 17 человек. Вероятность того, что второй француз попадёт в ту же группу, что и первый, равна

В среднем из 1000 садовых насосов, поступивших в продажу, 5 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.

Фабрика выпускает сумки. В среднем на 100 качественных сумок приходится 3 сумки со скрытыми дефектами. Найдите вероятность того, что случайно выбранная в магазине сумка окажется качественной.

В первом случае 1000 - вся выборка,

5 неисправных среди всех 1000 садовых насосов;

а во втором вся выборка 103, из нее 100 качественные

В чем­пи­о­на­те мира участ­ву­ют 16 ко­манд. С по­мо­щью жре­бия их нужно раз­де­лить на че­ты­ре груп­пы по че­ты­ре ко­ман­ды в каж­дой. В ящике впе­ре­меш­ку лежат кар­точ­ки с но­ме­ра­ми групп:

  1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4.

  Ка­пи­та­ны ко­манд тянут по одной кар­точ­ке. Ка­ко­ва ве­ро­ят­ность того , что ко­ман­да Рос­сии ока­жет­ся во вто­рой груп­пе?

Ве­ро­ят­ность того, что ко­ман­да Рос­сии ока­жет­ся во вто­рой груп­пе, равна от­но­ше­нию ко­ли­че­ства кар­то­чек с но­ме­ром 2, к об­ще­му числу кар­то­чек.

В Вол­шеб­ной стра­не бы­ва­ет два типа по­го­ды: хо­ро­шая и от­лич­ная, причём по­го­да, уста­но­вив­шись утром, дер­жит­ся не­из­мен­ной весь день. Из­вест­но, что с ве­ро­ят­но­стью 0,8 по­го­да зав­тра будет такой же, как и се­год­ня. Се­год­ня 3 июля, по­го­да в Вол­шеб­ной стра­не хо­ро­шая. Най­ди­те ве­ро­ят­ность того, что 6 июля в Вол­шеб­ной стра­не будет от­лич­ная по­го­да.

Для по­го­ды на 4, 5 и 6 июля есть 4 ва­ри­ан­та: ХХО, ХОО, ОХО, ООО (здесь Х — хо­ро­шая, О — от­лич­ная по­го­да).

Ука­зан­ные со­бы­тия не­сов­мест­ные, ве­ро­ят­ность их суммы равна сумме ве­ро­ят­но­стей этих со­бы­тий: 

P(ХХО) + P(ХОО) + P(ОХО) + P(ООО) = 0,128 + 0,128 + 0,008 + 0,128 = 0,392.

Най­дем ве­ро­ят­но­сти на­ступ­ле­ния такой по­го­ды:

P(XXO) = 0,8·0,8·0,2 = 0,128;

P(XOO) = 0,8·0,2·0,8 = 0,128;

P(OXO) = 0,2·0,2·0,2 = 0,008;

P(OOO) = 0,2·0,8·0,8 = 0,128.

Двое играют в кости - они по разу бросают игральный кубик. Выигрывает тот, у кого больше очков. Если выпадает поровну, то наступает ничья. Первый бросил кубик, и у него выпало 4 очка. Найдите вероятность того, что он выиграет.

Первый выиграет, если у второго выпадет 1, 2 или 3.

В случайном эксперименте бросают две игральные кости.

Найдите вероятность того, что в сумме выпадет 6 очков

Строки – результат первого броска,

столбцы – второго

Правила комбинаторики

Правила комбинаторики

суммы

произведения

происходит

хотя бы одно из событий

происходят

оба события

А или В

А и В

У двух школьников по четыре шариковых ручки (красная, зелёная, синяя и чёрная). Они наугад обменялись одной ручкой. Какова вероятность того, что у одного из них окажется две ручки чёрного цвета?

• вероятность того, что первый школьник

станет обменивать чёрную ручку

• вероятность того, что второй школьник станет

обменивать ручку другого цвета

-

Вероятность того, что обе чёрные ручки окажутся у второго школьника

Т.к. по условию школьники

не пронумерованы,

то искомая вероятность

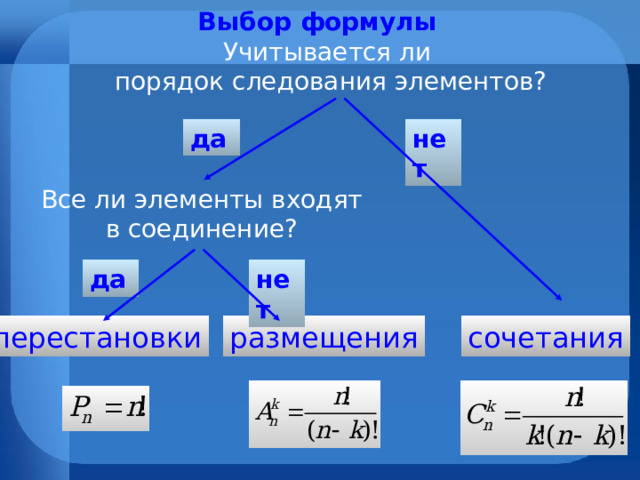
Выбор формулы

Учитывается ли

порядок следования элементов?

нет

да

Все ли элементы входят в соединение?

нет

да

перестановки

размещения

сочетания

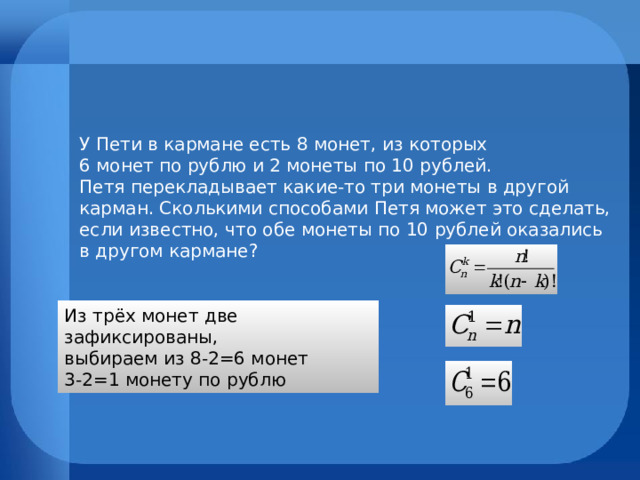
У Пети в кармане есть 8 монет, из которых 6 монет по рублю и 2 монеты по 10 рублей. Петя перекладывает какие-то три монеты в другой карман. Сколькими способами Петя может это сделать, если известно, что обе монеты по 10 рублей оказались в другом кармане?

Из трёх монет две зафиксированы,

выбираем из 8-2=6 монет

3-2=1 монету по рублю

В кармане у Пети было 4 монеты по рублю и 2 монеты по 2 рубля. Петя, не глядя, переложил какие-то три монеты в другой карман. Найдите вероятность того, что обе двухрублевые монеты лежат в одном кармане.

Возможны 2 варианта: либо Петя двухрублёвые монеты вообще не перекладывал, либо переложил сразу обе.

Если двухрублевые монеты не перекладывались, то 3 монеты по рублю можно выбрать из 4 способами.

Если обе двухрублевые монеты переложены, то еще одну рублевую монету можно выбрать из 4 способами.

Всего выбираем 3 монеты из 4+2=6 способами.

Чтобы пятирублевые монеты лежали в разных карманах, надо переложить только одну из них. Это можно сделать способами.

Всего Петя переложил 3 монеты, придется переложить еще 2 монеты по 10 рублей. Таких монет у Пети 4, поэтому количество способов равно

Переложить 3 монеты из 6 имеющихся можно способами.

2 способ

1

456

345

346

356

234

235

236

245

246

256

123

124

125

126

134

135

136

145

146

156

2

3

4

5

6