Презентация к лекции: Двойственность булевых функций. Теорема Поста

Повторение

Законы и тождества алгебры логики

1) Коммутативность конъюнкции и дизъюнкции

x  y = y  x x  y = y  x

2) Ассоциативность конъюнкции и дизъюнкции

x  ( y  z )= ( x  y )  z x  ( y  z )=( x  y )  z

3) Дистрибутивность конъюнкции и дизъюнкции относительно друг друга

x  (y  z) = (x  y)  (x  z)

x  (y  z) = (x  y)  (x  z)

Законы и тождества алгебры логики

4) Идемпотентность конъюнкции и дизъюнкции

x  x = х x  x = х

5) Закон исключенного третьего

6) Закон противоречия

8) Закон элиминации

x  ( x  y ) = х

x  ( x  y ) = х

1

0

Законы и тождества алгебры логики

7) Тождества с константами .

x  0 = х x  1 = х

x  1 = 1 x  0 = 0

9) Закон двойного отрицания .

10) Законы де Моргана .

x

Двойственность булевых функций. Теорема Поста.

План

• Двойственные булевы функции
• Самодвойственные булевы функции

Двойственные булевы функции

Функция f*(x 1 ,…,x n ) называется двойственной к функции f(x 1 ,…,x n ) , если

Пример построения двойственной функции

Пример

Най ти двойственные функции

Самодвойственные булевы функции

Функция, равная своей двойственной, называется самодвойственной .

f = f*

x

0

x

y

0

f(x,y)=f*(x,y)

0

y

0

1

f(0,0)= (1,1)

0

f(x,y)

1

0

1

1

f*(x,y)

1

f(0,1)= (1,0)

f(0,0)

0

1

(1,1)

0

f(1,0)= (0,1)

1

f(0,1)

1

f(1,0)

(1,0)

f(1,1)= (0,0)

f(1,1)

(0,1)

(0,0)

Пример

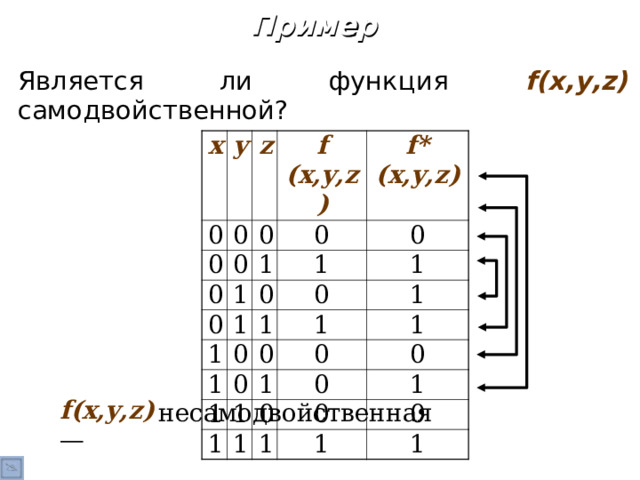
Является ли функция f(x,y,z) самодвойственной ?

x

y

0

z

0

0

0

f (x,y,z)

0

0

1

1

0

0

f* (x,y,z)

1

1

0

1

0

0

1

1

1

0

1

0

1

0

1

1

1

1

1

0

1

0

0

0

1

0

1

1

0

1

f(x,y,z) —

несамодвойственная

Принцип двойственности

Пусть функция F заданна суперпозицией функций f 0 ,…,f n , где n  N . Функцию F* , двойственную F , можно получить, заменив в формуле F функции f 0 ,…,f n на двойственные им f 0 * ,…,f n * .

Правило получения двойственных формул

Для того чтобы получить двойственную формулу булевой алгебры необходимо заменить в ней все конъюнкции на дизъюнкции, дизъюнкции на конъюнкции, 0 на 1, 1 на 0, и использовать скобки, где необходимо, чтобы порядок выполнения операций остался прежним .

Правило получения двойственных формул

Пример

Найти функцию, двойственную функции

Решение

Правило получения двойственных формул

Если функции равны, то и двойственные им функции также равны .

Пусть f 1 и f 2 – некоторые функции, заданные формулами. Тогда если

f 1 = f 2 ,

то

f 1 * = f 2 *

Замкнутые классы функций

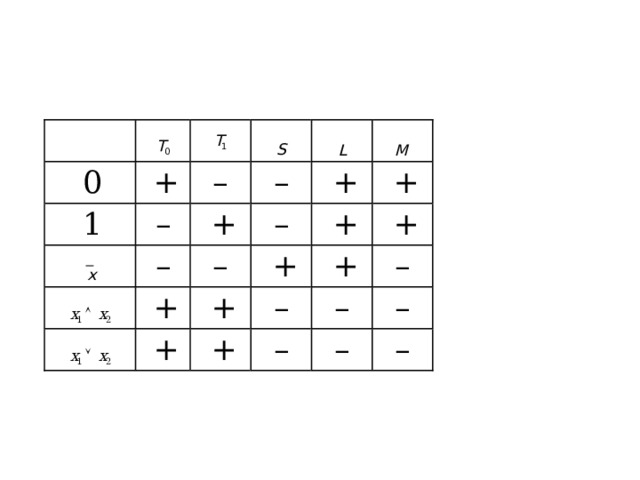
свойства замыкания:

Теорема Поста

Пример

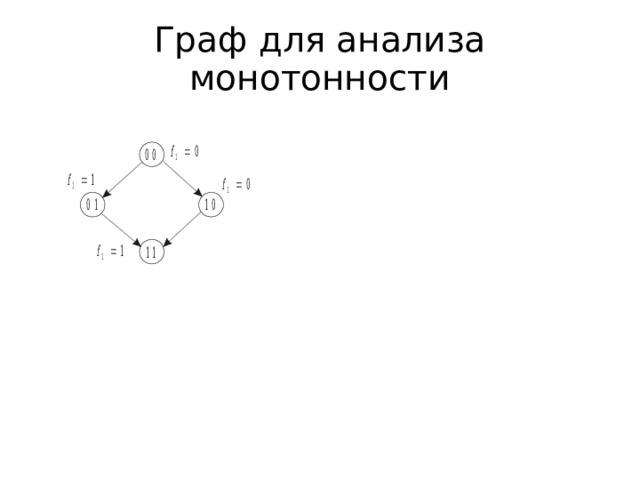
Граф для анализа монотонности

Вопросы.

• Какие функции называются двойственными?
• Какие функции называются самодвойственными?
• Как определить полному системы функций?

3. Является ли полной система