Презентация к лекции: Понятие алгоритма. Свойства алгоритма.

Понятие алгоритма.

Свойства алгоритма.

План

• Алгоритмы. Свойства алгоритмов.
• Способы записи алгоритмов.
• Анализ алгоритмов.
• Классификация алгоритмов по временной сложности.

ё

Алгоритм – происходит от Al Horithmi – латинского написания

арабского имени среднеазиатского математика IX века аль - Хорезми

IX век

Основатели теории алгоритмов

XX век

Возникает научное

н а п р а в л е н и е

ТЕОРИЯ АЛГОРИТМОВ

Направление исследований :

разработка универсальной

алгоритмической модели

1903 - 1979 г.

1912 - 1954 г.

787 – 850 г.

30 – е годы

С появлением ЭВМ (2-я половина XX века) понятие АЛГОРИТМА

связывается с ПРОГРАММИРОВАНИЕМ . Появляется большое

количество алгоритмических языков: Фортран, Паскаль, Бейсик . . .

ё

Алгоритм – происходит от Al Horithmi – латинского написания

арабского имени среднеазиатского математика IX века аль - Хорезми

IX век

Основатели теории алгоритмов

XX век

Возникает научное

н а п р а в л е н и е

ТЕОРИЯ АЛГОРИТМОВ

Направление исследований:

разработка универсальной

алгоритмической модели

1903 - 1979 г.

1912 - 1954 г.

787 – 850 г.

30 – е годы

В X I I веке в Европе вышел латинский перевод математического трактата аль – Хорезми . Алгоритмами назвали описанные в трактате правила выполнения арифметических вычислений в позиционной десятичной системе счисления.

В наше время понятие алгоритма понимается шире,

не ограничиваясь только арифметическими вычислениями.

4

4

ё

Алгоритм – происходит от Al Horithmi – латинского написания

арабского имени среднеазиатского математика IX века аль - Хорезми

XX век

Основатели теории алгоритмов

IX век

Возникает научное

н а п р а в л е н и е

ТЕОРИЯ АЛГОРИТМОВ

Направление исследований:

разработка универсальной

алгоритмической модели

1912 - 1954 г.

1903 - 1979 г.

30 – е годы

787 – 850 г.

Английский математик Алан Тьюринг в 1935 – 1936 годах создает теорию «логических вычисляющих машин». Разработанная им « Машина Тьюринга » стала обязательной частью обучения будущих математиков и компьютерщиков. На одной из лондонских гостиниц мемориальная доска гласит: «Здесь родился Алан Тьюринг (1912 – 1954), взломщик кодов и пионер информатики».

5

5

ё

Алгоритм – происходит от Al Horithmi – латинского написания

арабского имени среднеазиатского математика IX века аль - Хорезми

IX век

XX век

Основатели теории алгоритмов

Возникает научное

н а п р а в л е н и е

ТЕОРИЯ АЛГОРИТМОВ

Направление исследований:

разработка универсальной

алгоритмической модели

1903 - 1979 г.

1912 - 1954 г.

30 – е годы

787 – 850 г.

Русский математик Андрей Марков в 1947 году ввел понятие « нормального алгоритма » и впервые систематически и строго построил общую теорию алгоритмов. Современные языки символьной обработки (Пролог) берут свое начало от нормальных алгоритмов Маркова.

6

6

Правила выполнения арифметических действий над целыми числами и простыми дробями в десятичной системе счисления впервые были сформулированы выдающимся средневековым ученым по имени Мухаммед ибн Муса ал-Хорезми (в переводе с арабского это означает «Мухаммед, сын Мусы из Хорезма»), сокращенно Ал-Хорезми.

787 – 850 г.

Ал-Хорезми жил и творил в IX веке в г.Хива Хорезмской области Узбекистана. Арабский оригинал его арифметического труда утерян, но имеется латинский перевод XII века, по которому Западная Европа познакомилась с десятичной позиционной системой счисления и правилами выполнения в ней арифметических действий.

6

6

Алан Тьюринг

Английский математик Алан Тьюринг в 1935 – 1936 годах создает теорию «логических вычисляющих машин». Разработанная им « Машина Тьюринга » стала обязательной частью обучения будущих математиков и компьютерщиков.

На одной из лондонских гостиниц мемориальная доска гласит: «Здесь родился Алан Тьюринг (1912 – 1954), взломщик кодов и пионер информатики».

1912 - 1954 г.

6

6

Андрей Марков

Русский математик Андрей Марков в 1947 году ввел понятие « нормального алгоритма » и впервые систематически и строго построил общую теорию алгоритмов.

Современные языки символьной обработки (Пролог) берут свое начало от нормальных алгоритмов Маркова.

1903 - 1979 г.

6

6

Алгоритм – понятное и точное предписание исполнителю совершить последовательность действий, направленных на достижение определенной цели или на решение поставленной задачи.

1.Налить в чайник воду.

2.Зажечь газовую горелку.

3.Поставить на нее чайник.

4.Подождать пока вода в чайнике закипит.

5.Отключить газ.

6.В заварной чайник насыпать 2-3 чайные ложки заварки.

7.Залейте кипятком и пусть настоится 5 минут.

8.В чашки налейте немного заварки, затем кипяток.

9.Положите сахар по вкусу.

Задание . Вы захотели выпить чашечку чаю. Запишите порядок своих действий.

6

6

С войства алгоритма:

Понятность – каждый шаг алгоритма должен быть понятен исполнителю;

Дискретность (прерывность, раздельность) – разбиение алгоритма на шаги;

Конечность - выполняемый алгоритм должен приводиться к результату за конечное число шагов;

Результативность - получение результата за конечное число шагов;

Массовость – использование алгоритма для решения однотипных задач.

Формальность – возможность выполнять команды механически.

Это свойство позволяет поручить исполнение алгоритмов роботам, компьютерам и другим устройствам.

6

6

Свойства алгоритма

Понятность. Каждая команда должна быть понятна тому, кто исполняет алгоритм (исполнителю). Полный список команд, которые умеет выполнять исполнитель называется системой команд исполнителя (СКИ)

6

6

Свойства алгоритма

Дискретность. Процесс решения задачи должен быть разбит на последовательность отдельных шагов, следующих в определенном порядке, каждый из которых называется командой.

6

6

Свойства алгоритма

Конечность (результативность). Результат выполнения алгоритма должен быть обязательно получен. Кроме того, любой алгоритм должен завершиться за конечное число шагов.

6

6

Свойства алгоритма

Массовость. Это возможность применения алгоритма для решения целого класса конкретных задач, отвечающих общей постановке задачи. Иными словами, алгоритм имеет смысл разрабатывать, только в том случае если он будет применяться для различных наборов исходных данных.

Перед Вами формула, которая используется в физике для расчета общего сопротивления двух или более проводников соединенных параллельно.

Эта формула – есть не что иное как алгоритм нахождения общего сопротивления. Меняя исходные данные сопротивлений и их количество, можно находить результаты для нового набора данных.

6

6

Свойства алгоритма

Детерминированность, Формальность (определенность). Команды, образующие алгоритм должны быть предельно четкими и однозначными

6

6

Виды алгоритмов:

Линейный алгоритм – это описание действий, которые выполняются однократно в заданном порядке.

Разветвляющийся алгоритм - это алгоритм, в котором в зависимости от условия выполняется либо одна, либо другая последовательность действий.

Циклический – это описание действий, которые должны повторяться указанное число раз или пока не выполнено заданное условие. (параметра цикла).

6

6

Линейные алгоритмы состоят из нескольких команд (операторов), которые должны быть выполнены последовательно одна за другой .

Структура линейного алгоритма

Команда 1

Команда 2

. . .

Команда N

18

18

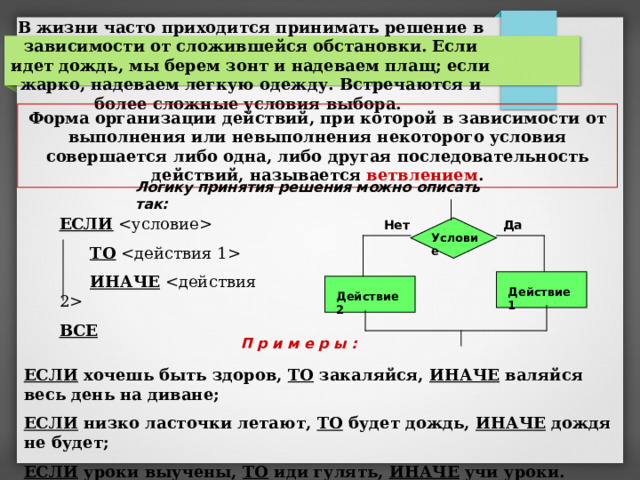
В жизни часто приходится принимать решение в зависимости от сложившейся обстановки. Если идет дождь, мы берем зонт и надеваем плащ; если жарко, надеваем легкую одежду. Встречаются и более сложные условия выбора.

Форма организации действий, при которой в зависимости от выполнения или невыполнения некоторого условия совершается либо одна, либо другая последовательность действий, называется ветвлением .

Логику принятия решения можно описать так:

ЕСЛИ

ТО

ИНАЧЕ

ВСЕ

Да

Нет

Условие

Действие 1

Действие 2

П р и м е р ы :

ЕСЛИ хочешь быть здоров, ТО закаляйся, ИНАЧЕ валяйся весь день на диване;

ЕСЛИ низко ласточки летают, ТО будет дождь, ИНАЧЕ дождя не будет;

ЕСЛИ уроки выучены, ТО иди гулять, ИНАЧЕ учи уроки.

19

19

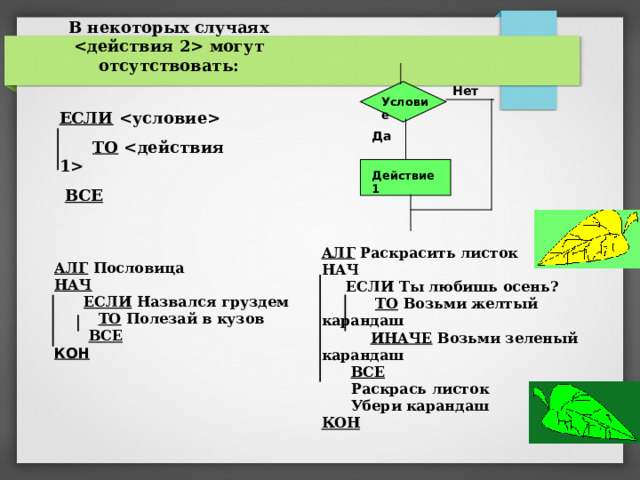могут отсутствовать: Нет Условие ЕСЛИ условие ТО действия 1 ВСЕ Да Действие 1 АЛГ Раскрасить листок НАЧ ЕСЛИ Ты любишь осень? ТО Возьми желтый карандаш ИНАЧЕ Возьми зеленый карандаш ВСЕ Раскрась листок Убери карандаш КОН АЛГ Пословица НАЧ ЕСЛИ Назвался груздем ТО Полезай в кузов ВСЕ КОН 20 20 " width="640"

В некоторых случаях действия 2 могут отсутствовать:

Нет

Условие

ЕСЛИ условие

ТО действия 1

ВСЕ

Да

Действие 1

АЛГ Раскрасить листок

НАЧ

ЕСЛИ Ты любишь осень?

ТО Возьми желтый карандаш

ИНАЧЕ Возьми зеленый карандаш

ВСЕ

Раскрась листок

Убери карандаш

КОН

АЛГ Пословица

НАЧ

ЕСЛИ Назвался груздем

ТО Полезай в кузов

ВСЕ

КОН

20

20

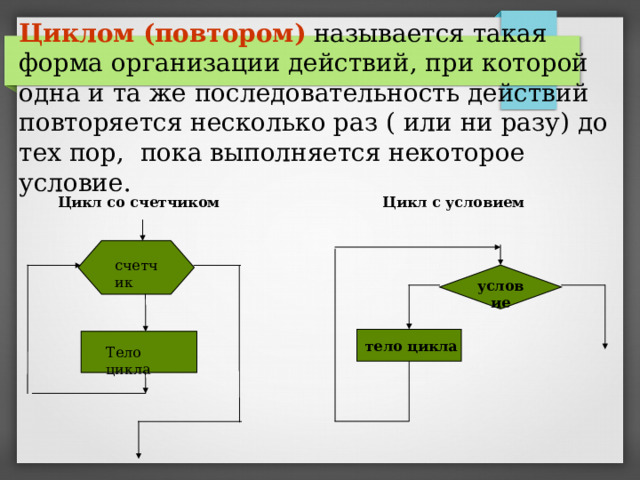
Циклом (повтором) называется такая форма организации действий , при которой одна и та же последовательность действий повторяется несколько раз ( или ни разу) до тех пор, пока выполняется некоторое условие.

Цикл со счетчиком

Цикл с условием

счетчик

условие

тело цикла

Тело цикла

21

21

Алгоритмы можно записывать разными способами, называемыми формой представления алгоритма . На практике наиболее распространены следующие формы представления алгоритмов:

• словесная (записи на естественном языке);
• графическая (стрелки, изображения, блок-схемы);
• псевдокоды (полуформализованные описания алгоритмов на условном алгоритмическом языке, включающие в себя как элементы языка программирования, так и фразы естественного языка, общепринятые математические обозначения и др.);
• программная (тексты на языках программирования).

2.Способы записи алгоритмов:

21

21

Словесная форма записи алгоритмов обычно используется для алгоритмов, ориентированных на исполнителя-человека. Команды такого алгоритма выполняются в естественной последовательности, если не оговорено противного.

Примеры записи алгоритмов на естественном языке.

Алгоритм « Набери в лесу грибов »

1.Возьми пустую корзину.

2.Прийди в лес.

3.Если нашел съедобный гриб, то положи в корзину.

4.Если корзина еще не полная, то повтори п.3, иначе перейди к п.5.

5.Приди домой.

6.Поставь корзину с грибами на место.

Алгоритм « Съешь конфету»

1.Возьми конфету из вазы.

2.Разверни фантик.

3.Съешь конфету.

4.Фантик выбрось в мусорное ведро.

Алгоритм « Рисунок »

1.Возьми карандаш.

«Если ты любишь рисовать, то нарисуй яблоко, иначе напиши чем ты любишь заниматься».

21

21

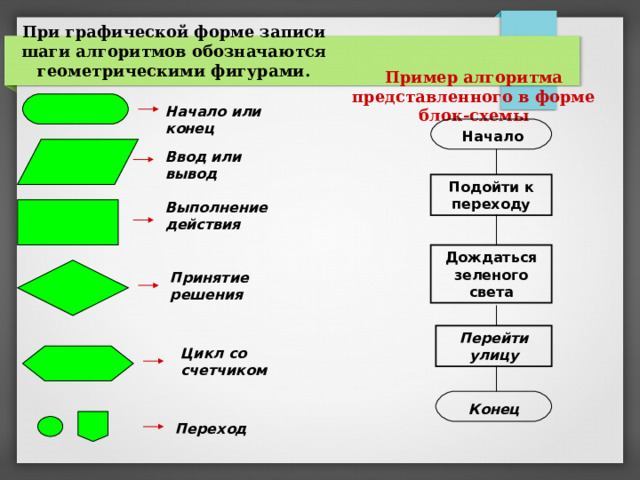
При графической форме записи шаги алгоритмов обозначаются геометрическими фигурами.

Пример алгоритма представленного в форме блок-схемы

Начало или конец

Начало

Ввод или вывод

Подойти к переходу

Выполнение действия

Дождаться зеленого света

Принятие решения

Перейти улицу

Цикл со счетчиком

Конец

Переход

24

24

НАЧ Ввод Исходные данные Серия команд Вывод Результат КОН Примеры записи алгоритмов на алгоритмическом языке. АЛГ Дождь НАЧ Подойди к окну ЕСЛИ Идет дождь ТО Останься дома ИНАЧЕ Иди гулять ВСЕ КОН АЛГ Вычислить Y=R+T-X НАЧ Ввод R,T,X A1:= R+T Y:= A1-X Вывод Y КОН 25 25 " width="640"

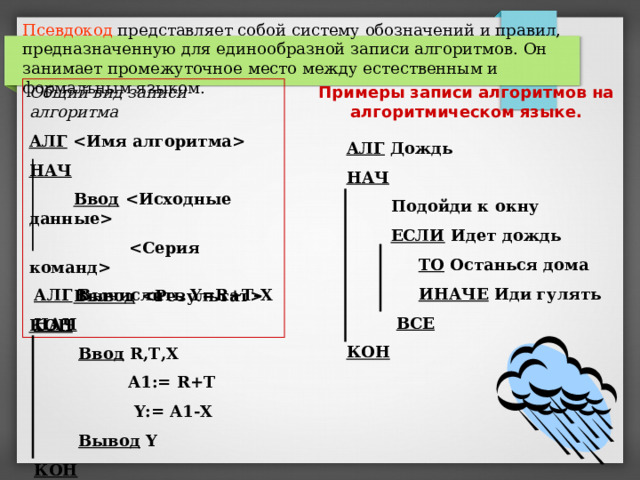
Псевдокод представляет собой систему обозначений и правил, предназначенную для единообразной записи алгоритмов. Он занимает промежуточное место между естественным и формальным языком.

Общий вид записи алгоритма

АЛГ Имя алгоритма

НАЧ

Ввод Исходные данные

Серия команд

Вывод Результат

КОН

Примеры записи алгоритмов на алгоритмическом языке.

АЛГ Дождь

НАЧ

Подойди к окну

ЕСЛИ Идет дождь

ТО Останься дома

ИНАЧЕ Иди гулять

ВСЕ

КОН

АЛГ Вычислить Y=R+T-X

НАЧ

Ввод R,T,X

A1:= R+T

Y:= A1-X

Вывод Y

КОН

25

25

b then max:=a else max:=b; writeln (max); End. Алгоритм , записанный на понятном компьютеру языке программирования , называется программой. 25 25 " width="640"

Program ostatok;

Uses crt;

Var a, b, max: real;

Begin

ClrScr;

Readln (a, b);

If ab

then max:=a

else max:=b;

writeln (max);

End.

Алгоритм , записанный на понятном компьютеру языке программирования , называется программой.

25

25

3.Анализ алгоритма

Анализ предполагает доказательство правильности алгоритма и определение его временных характеристик, т.е. установление того, как быстро алгоритм решает задачу.

Под правильностью алгоритма понимают то, что он правильно решает задачу.

1. Теоретический.

2.Экспериментальный.

25

25

4.Анализ алгоритма

Теоретический.

1.1. Метод прямого перебора

(Пример n! )

1.2.Доказательство правильности каждого шага алгоритма с последующим доказательством конечности его шагов.

(Прогон программы на контрольных примерах)

25

25

4.Анализ алгоритма

2.Экспериментальный.

2.1. Прогон программы на разных, заранее подготовленных контрольных тестах.

2.2. Оценка временных характеристик.

25

25

4.Классификация алгоритмов по временной сложности

1.Полиномиальные

2.Экспоненциальные

25

25

Преимущества полиномиальных алгоритмов

1.При увеличении размера задачи время счета по этим алгоритмам растет значительно медленнее, чем по экспоненциальным, даже в том случае, когда для малых n полиномиальный алгоритм затрачивает больше времени, чем экспоненциальный

25

25

Преимущества полиномиальных алгоритмов

2.Полиномиальные алгоритмы лучше используют технологии производства компьютеров, направленные на повышение их производительности. (При увеличении производительности компьютера в 10 раз, размер задач, решаемых полиномиальным алгоритмов увеличивается в 1

25

25

Преимущества полиномиальных алгоритмов

3. Алгоритмы полиномиальной допускают различные комбинации полиномиальных процедур не выходя за рамки своего класса.

25

25

Вопросы:

• С какими типами алгоритмов

Вы познакомились сегодня?

2. Почему они так называются?

25

25