Презентация к серии уроков по теме "Смежные и вертиуальные углы". Урок 2

Тема: Решение задач по теме: «Смежные углы»

Учитель математики ВКК

МБОУ БГО Борисоглебской СОШ №4 Конева Надежда Александровна

Тема: Решение задач по теме: «Смежные углы»

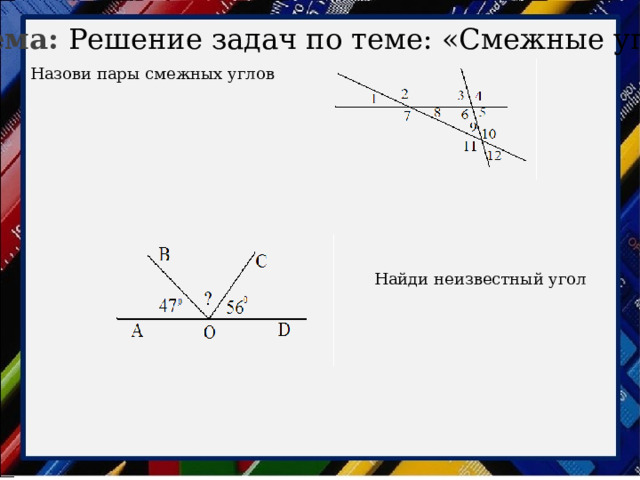
Назови пары смежных углов

Найди неизвестный угол

Тема: Решение задач по теме: «Смежные углы»

Мини проект об истории смежных углов

0

Тема: Решение задач по теме: «Смежные углы»

Следствия из теоремы:

Дано:∠1 = ∠2= α, ∠1 и ∠3 –смежные

∠ 2 и ∠4 – смежные

Доказать: ∠4=∠3

Доказательство:

1)∠1 =∠2 =α

2) ∠1+ ∠3=180 0 (смежные),

следовательно, ∠3=180 0 - ∠1=180 0 – α

3) ∠4+∠2 =180 0 (смежные),

следовательно, ∠4=180 0 - ∠2=180 0 – α

4) Вывод: ∠4= ∠3

Тема: Решение задач по теме: «Смежные углы»

№ 6(1). Найти смежные углы, если их градусные меры относятся как 2:3.

Решение: 1)Пусть ∠1 :∠2 как 2:3, тогда ∠1 = 2х 0 , ∠2 =3х 0 .

2) ∠1 +∠2=180 0 (по свойству смежных углов)

2х+3х=180

5х=180

х=36

3) ∠1 = 72 0 , ∠2 =108 0

Ответ: ∠1 = 36 0 , ∠2 =108 0

.

Тема: Решение задач по теме: «Смежные углы»

Самостоятельная работа

1вариант 2вариант

1. Могут ли два смежных угла быть равными:

а)65 0 и 115 0 а) 91 0 и 99  

б)72 0 и 88 б)136 и 44

2. Дано: ∠АВС и ∠СВD-смежные

∠ АВС в 5 раз больше ∠СВD

Найти: ∠АВС и ∠СВD

2. Дано: ∠МND и ∠KND-смежные

∠ МND на 50 0 меньше ∠KND

Найти: ∠МND и ∠KND

3.Построить угол, смежный с острым.

3.Построить угол, смежный с

тупым.

Домашнее задание:

п. 14, контрольные вопросы 3-5

№ 6(2-3)

Использованные источники: