«Великая книга природы может быть прочтена только теми, кто знает язык, на котором она написана, и этот язык – математика»
Галилео Галилей
(1564 – 1642)
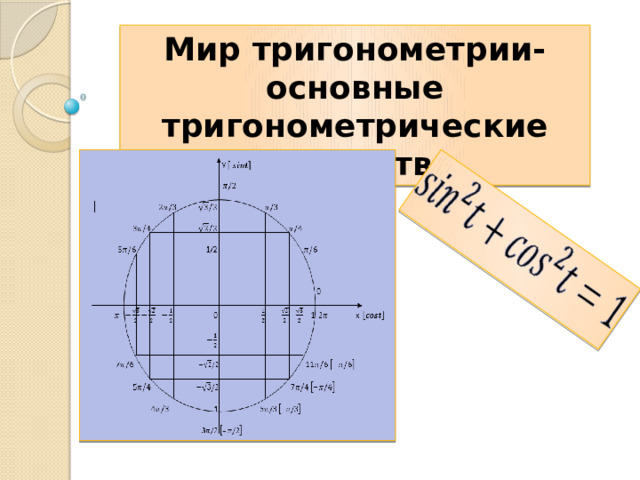
Мир тригонометрии- основные тригонометрические тождества

Мир тригонометрии- основные тригонометрические тождества
Цель урока: систематизация уже имеющихся знаний по тригонометрии, отработка навыков преобразования тригонометрических выражений.
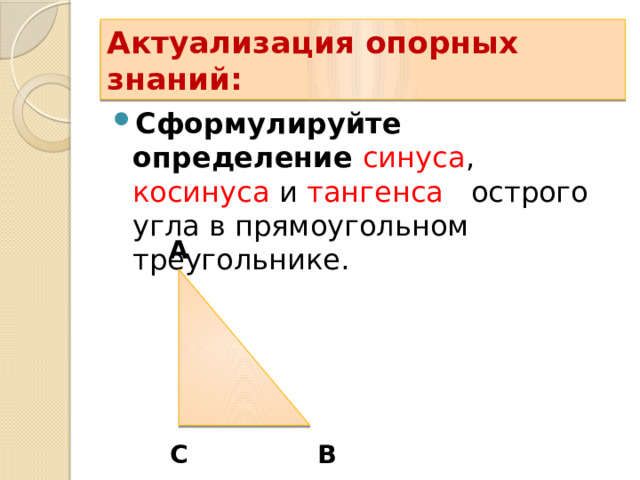
Актуализация опорных знаний:
- Сформулируйте определение синуса , косинуса и тангенса острого угла в прямоугольном треугольнике.
A
C
B

Актуализация опорных знаний:
- Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
- Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
- Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
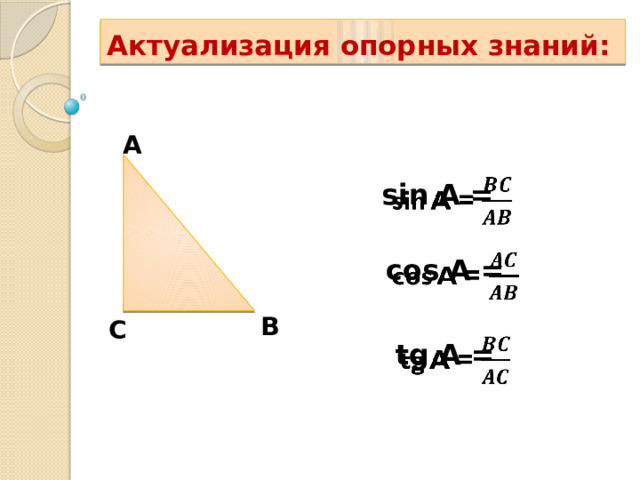
Актуализация опорных знаний:
A
sin A =
cos A =
B
C
tg A =
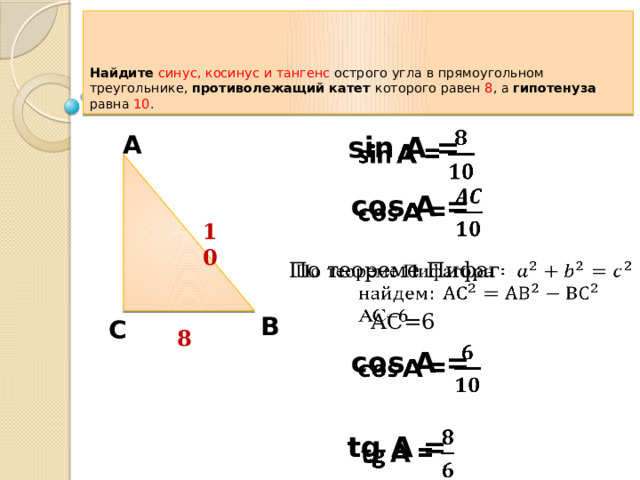
Найдите синус, косинус и тангенс острого угла в прямоугольном треугольнике, противолежащий катет которого равен 8 , а гипотенуза равна 10 .
sin A =
A
cos A =
10
По теореме Пифаг
АС=6
B
C
8
cos A =
tg A =

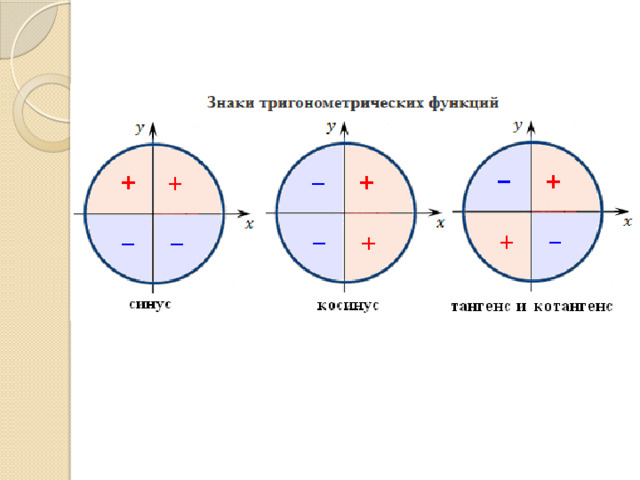
Назовите знаки тригонометрических функций по четвертям.
I четверть: 0
II четверть:
III четверть:
IV четверть:

Что такое 1 радиан?

Актуализация опорных знаний:
Перевести:
- в радианы: 30°,45°,60°,90°,270°,
-720°.

Переход от градусной меры углов к радианной Переход от радианной меры углов к градусной
Вариант №1 - ЛЛЛ
1. Переведите данные числа из градусной меры в радианную меру: ,
2. Переведите данные числа из радианной меры в градусную: п/6
Вариант №2
1. Переведите данные числа из градусной меры в радианную меру: ,
2. Переведите данные числа из радианной меры в градусную: п/10
Вариант №3 - ППП
1. Переведите данные числа из градусной меры в радианную меру: ,
2. Переведите данные числа из радианной меры в градусную: 5.

Зачем нам нужна тригонометрия
950
а
х

Тригономе́трия
- (от греч. τρίγονο (треугольник ) и греч. μετρειν ( измерять ), то есть измерение треугольников ) — раздел математики, в котором изучаются тригонометрические функции и их приложения к геометрии. Данный термин впервые появился в 1595 г. как название книги немецкого математика Бартоломеуса Питискуса (1561—1613), а сама наука ещё в глубокой древности использовалась для расчётов в астрономии, геодезии и архитектуре.
Тригонометрия – слово греческое и в переводе означает «измерение треугольников». Возникновение тригонометрии связано с измерениями на земле, строительным делом, астрономией. А первое знакомство с ней произошло тогда, когда вы взяли в руки транспортир.
13

Первые тригонометрические таблицы были, вероятно, составлены Гиппархом Никейским (180—125 лет до н. э.). Гиппарх был первым, кто свёл в таблицы соответствующие величины дуг и хорд для серии углов. Систематическое использование полной окружности в 360° установилось в основном благодаря Гиппарху и его таблице хорд.

Леонард Эйлер (1707 – 1783)
Иоганн Бернулли (1642-1727 )

Разделы тригонометрии
- Тригонометрия делится на плоскую, или прямолинейную, и сферическую тригонометрию .
- Теория тригонометрических функций (гониометрия) и её приложения к решению плоских прямоугольных и косоугольных треугольников мы с вами изучаем в основной школе

Основные формулы плоской тригонометрии
Теорема синусов:
Теорема косинусов:
В IV-V веках появился уже специальный термин в трудах по астрономии великого индийского учёного Ариабхаты, именем которого назван первый индийский спутник Земли. Дугу он назвал ардхаджива (ардха – половина, джива – тетива лука, которую напоминает хорда). Позднее появилось более краткое название джива. Арабскими математиками в IX веке это слово было заменено на арабское слово джайб (выпуклость). При переводе арабских математических текстов в веке оно было заменено латинским синус (sinus – изгиб, кривизна).
Слово косинус намного моложе. Косинус – это сокращение латинского выражения completely sinus, т. е. “дополнительный синус” (или иначе “синус дополнительной дуги”; cosa = sin( 90° - a)).
13

Сферическая тригонометрия, являющаяся частью сферической геометрии, рассматривает соотношения между сторонами и углами треугольников на сфере, образованных дугами больших кругов на сфере.
Исторически сферическая тригонометрия и геометрия возникли из потребностей астрономии, геодезии, навигации, картографии. Подумайте, какое из этих направлений в последние годы получило столь бурное развитие, что его результат уже применяется в современных коммуникаторах. … Современное применение навигации – это система спутниковой навигации, которая позволяет определить местоположение и скорость объекта по сигналу его приемника.
13
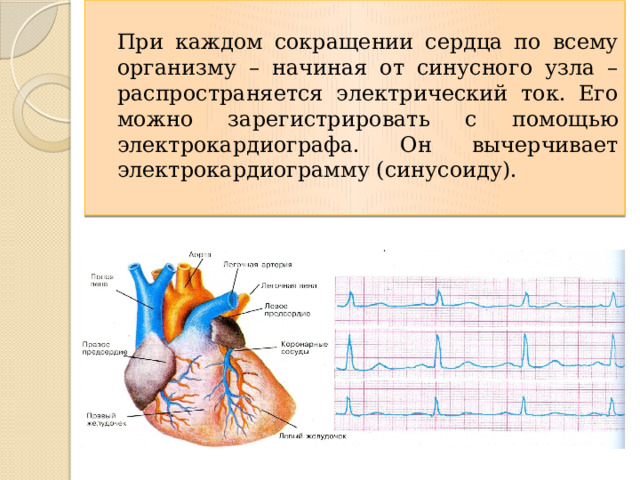
При каждом сокращении сердца по всему организму – начиная от синусного узла – распространяется электрический ток. Его можно зарегистрировать с помощью электрокардиографа. Он вычерчивает электрокардиограмму (синусоиду).
Давайте прислушаемся к биению своего сердца. Сердце – самостоятельный орган. Головной мозг управляет любой нашей мышцей, кроме сердечной. У нее есть собственный центр управления – синусный узел. При каждом сокращении сердца по всему организму – начиная от синусного узла (размером с просяное зерно)– распространяется электрический ток. Его можно зарегистрировать с помощью электрокардиографа. Он вычерчивает электрокардиограмму (синусоиду)
13
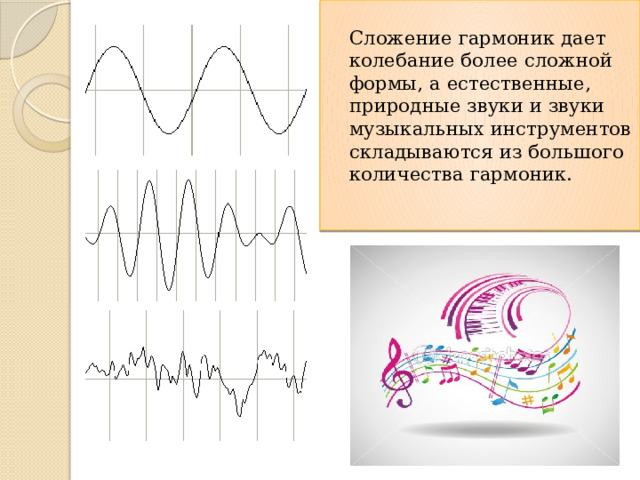
Сложение гармоник дает колебание более сложной формы, а естественные, природные звуки и звуки музыкальных инструментов складываются из большого количества гармоник.
Теперь поговорим о музыке. Математика – это музыка, это союз ума и красоты. Музыка – это математика по вычислениям, алгебра по абстрагированию, тригонометрия по красоте. Гармоническое колебание (гармоника) – это синусоидальное колебание.
13

Почему летом теплее, чем зимой?
- Все дело в наклоне земной оси по отношению к плоскости земной орбиты
- Зимой в умеренных широтах солнце невысоко поднимается над горизонтом, его лучи лишь скользят по земле. Летом в моменты наивысшего подъёма над горизонтом солнце приближается к зениту, его лучи падают почти отвесно на те же участки земного шара.
- ПОТОК ЭНЕРГИИ, ИДУЩЕЙ ОТ Солнца, одинаков во все времена года. Но в зависимости от наклона солнечных лучей она по-разному распределяется по земной поверхности.
Все дело в наклоне земной оси по отношению к плоскости земной орбиты
Именно эту зависимость применяет курортник, загорающий под солнцем юга, когда он поворачивает свой топчан так, чтобы солнечные лучи как можно менее отклонялись от перпендикуляра к плоскости топчана.
13

Сферы
применения
- Астрономия
- Геодезия
- Картография
- Механика
- Оптика
- Акустика
- Строительство
- Архитектура
- Дизайн
- Навигация
- Медицина
- Музыка
- Спорт
ТРИГОНОМЕТРИЯ
13

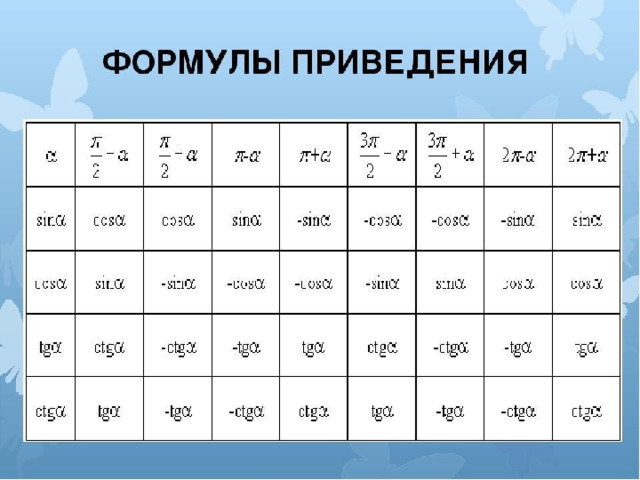
Формулы приведения
y
π/2+t π/2 π/2-t
1) Определить четверть
π – t 2π+t 2) Определить знак функции
π х 3) От ОХ – не меняем на кофункцию
2π-t
π+t 4) От ОУ – меняем на кофункцию.
3π/2-t 3π/2 3π/2+t

Формулы приведения
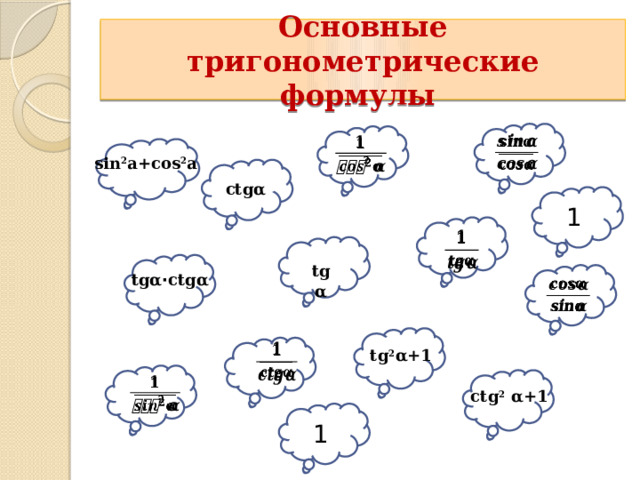
Основные тригонометрические формулы
sin 2 a+cos 2 a
сtgα
1
tgα
tgα ⋅ ctgα
tg 2 α+1
ctg 2 α+1
1

Основные тригонометрические формулы
sin 2 a+cos 2 a
сtgα
1
tgα
tgα ⋅ ctgα
tg 2 α+1
ctg 2 α+1
1

Основные тригонометрические формулы

Тест
1 вариант
2 вариант
Упростить выражение:
7 cos 2 а +7 sin 2 а - 5
а) 1+cos 2 а; б) 2; в) –12; г) 12
2) Упростить выражение:
5 – 4 sin 2 а - 4cos 2 а
а) 1; б) 9; в) 1+8sin 2 а; г) 1+cos 2 а.
3) Упростить выражение:
(1 – cos 2 а): cos 2 а – tg 2 а
а) ctg 2 а; б) 0; в) ctg 2 а - tg 2 а; г) 2tg 2 а
4) Упростить выражение
cos 4 х + sin 2 х·cos 2 х
а) cos 2 x; б) 2sin 2 х; в)- cos 2 х;
г) cos 4 х
9 cos 2 а+ 9 sin 2 а - 10
а) -1; б) 0; в) sin 2 а; г) 10
2) Упростить выражение:
8 – 3 sin 2 а - 3cos 2 а
а)1+ sin 2 а; б) cos 2 а-1; в) 1; г) 5
3) Упростить выражение:
(1 – sin 2 а): sin 2 а– сtg 2 а
а) sin 2 а ; б) 0; в) 2сtg 2 а; г) sin 2 а
4) Упростить выражение
sin 4 х + sin 2 х·cos 2 х
а) sin 4 х; б) 2sin 2 х; в) sin 2 x;
г) cos 2 x

Тригонометрия –
это просто и понятно !
Ответы:
Вариант 1: 1а, 2г, 3б, 4в Вариант 2: 1б, 2а, 3б, 4а
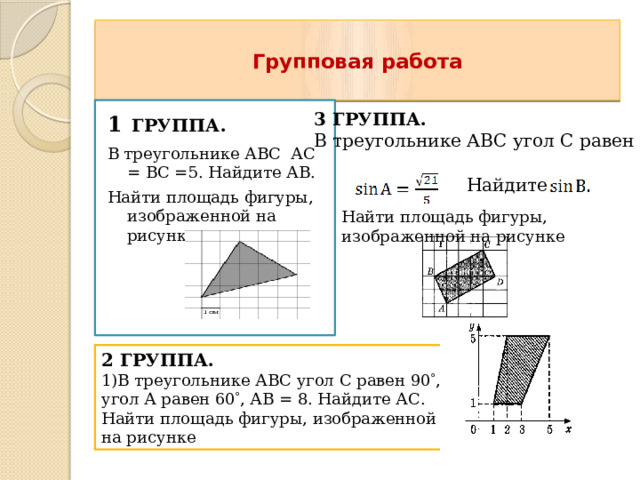
Групповая работа
1 ГРУППА.
В треугольнике АВС АС = ВС =5. Найдите АВ.
Найти площадь фигуры, изображенной на рисунке
3 ГРУППА.
В треугольнике АВС угол С равен 90 ,
Найдите
Найти площадь фигуры, изображенной на рисунке
2 ГРУППА.
1)В треугольнике АВС угол С равен 90 , угол А равен 60 , АВ = 8. Найдите АС.
Найти площадь фигуры, изображенной на рисунке
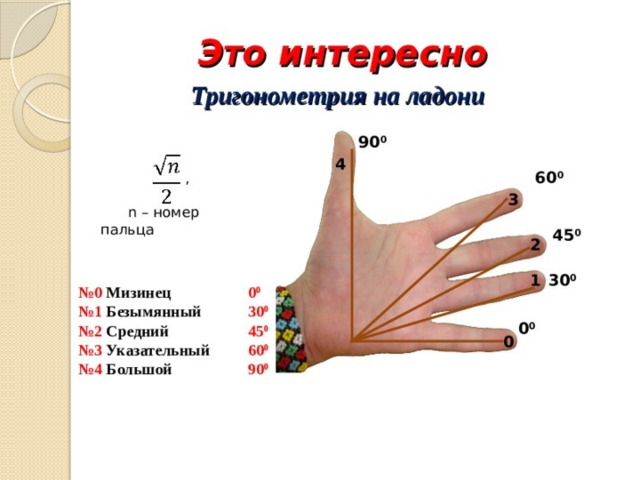

Это интересно!

Подведение итогов урока:
Сегодня на уроке
я повторил …
Сегодня на уроке
я научился …
Мне необходимо
еще поработать над …
Сегодня на уроке мне понравилось…
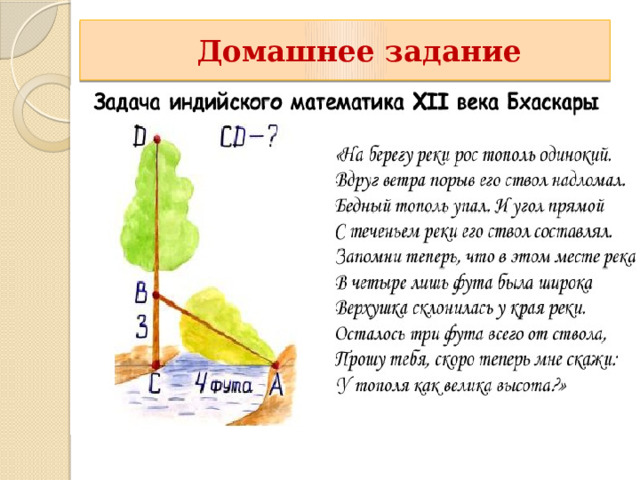
Домашнее задание
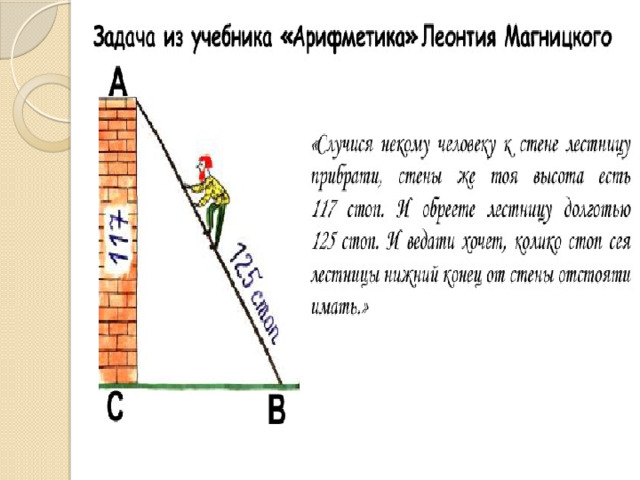

Проверь себя
Найти ширину
реки.
х
а

Башня
Измерить высоту
a
h