Презентация к уроку алгебры на тему "Возрастание и убывание функции" (11 класс)

11 класс Алгебра Возрастание и убывание функции

Автор презентации: Попов Дмитрий Сергеевич

Сегодня мы поговорим о возрастании и убывании функции. Как вы знаете, эта тема достаточно важна, потому что встречается на ЕГЭ, во вступительных экзаменах. Сложная ли она? И да, и нет. Но не беспокойтесь, сегодня мы обязательно во всем разберемся!

Вспомним определение функции:

Функция — это взаимосвязь между величинами, то есть зависимость одной переменной величины от другой.

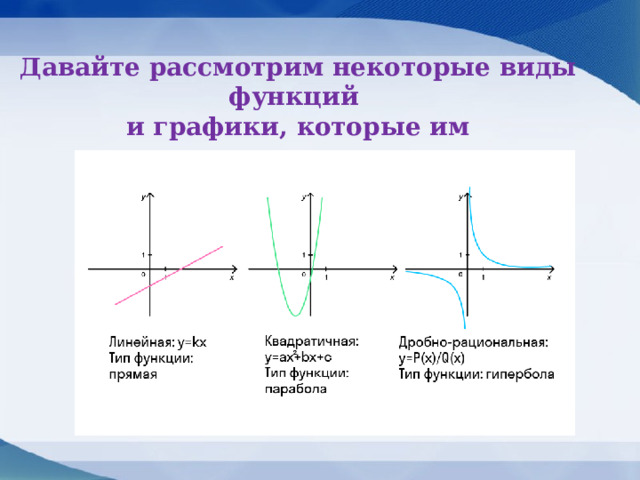
Давайте рассмотрим некоторые виды функций и графики, которые им соответствуют:

В исследовании функции особое значение уделяют ее поведению в системе координат — монотонности функции. Функции бывают монотонными, немонотонными и постоянными .

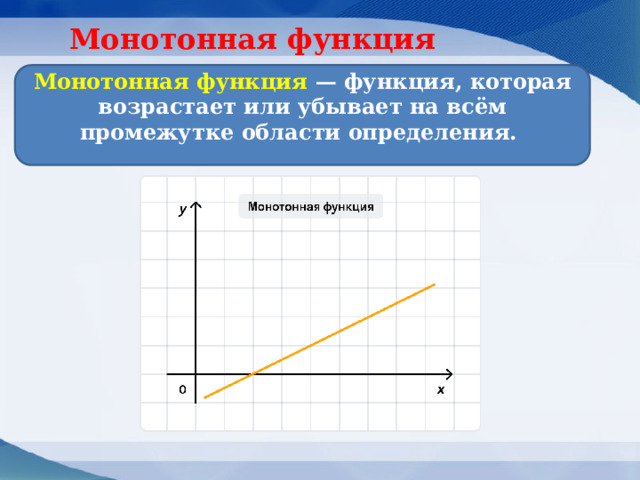
Монотонная функция

Монотонная функция — функция, которая возрастает или убывает на всём промежутке области определения.

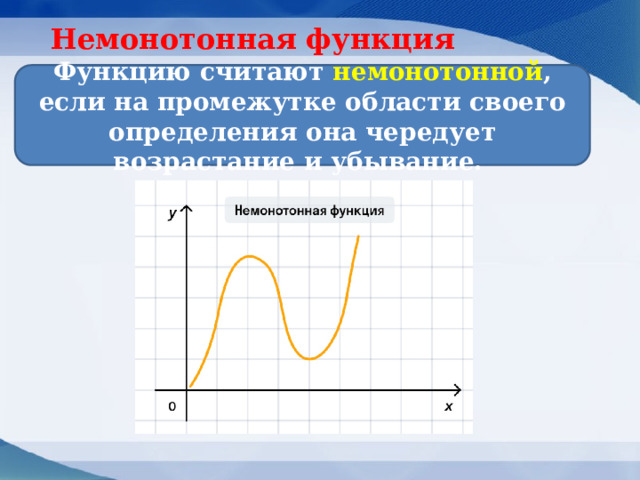
Немонотонная функция

Функцию считают немонотонной , если на промежутке области своего определения она чередует возрастание и убывание.

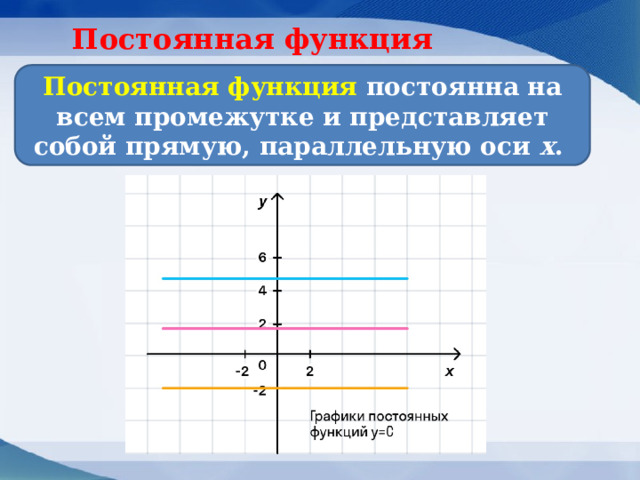
Постоянная функция

Постоянная функция постоянна на всем промежутке и представляет собой прямую, параллельную оси x .

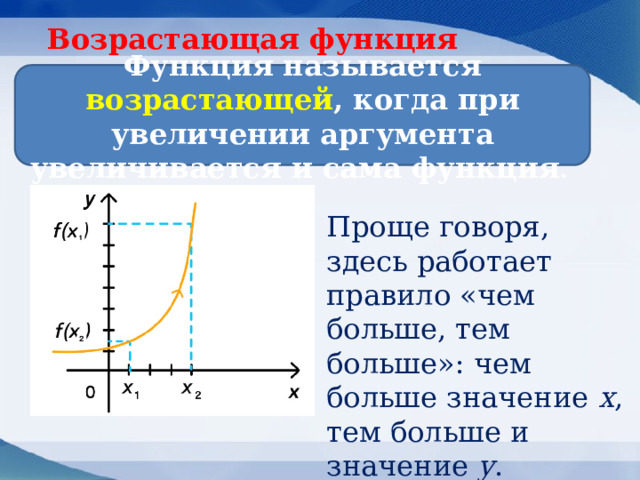
Возрастающая функция

Функция называется возрастающей , когда при увеличении аргумента увеличивается и сама функция .

Проще говоря, здесь работает правило «чем больше, тем больше»: чем больше значение х , тем больше и значение у .

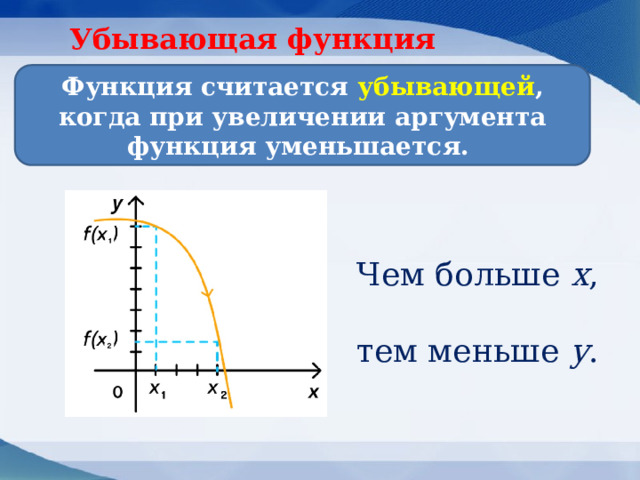
Убывающая функция

Функция считается убывающей , когда при увеличении аргумента функция уменьшается.

Чем больше х , тем меньше у .

Определим, возрастающая или убывающая функция y = 2 x + 3.

Определите, возрастающая или убывающая функция y = 2 x + 3.

• Найдем область определения функции: х ∈ R.
• Найдем координаты нескольких точек, которые ей принадлежат.

x

y

0

1

3

2

6

3

7

9

Как вы уже заметили, значения х и у одновременно увеличиваются — функция возрастает на всем промежутке.

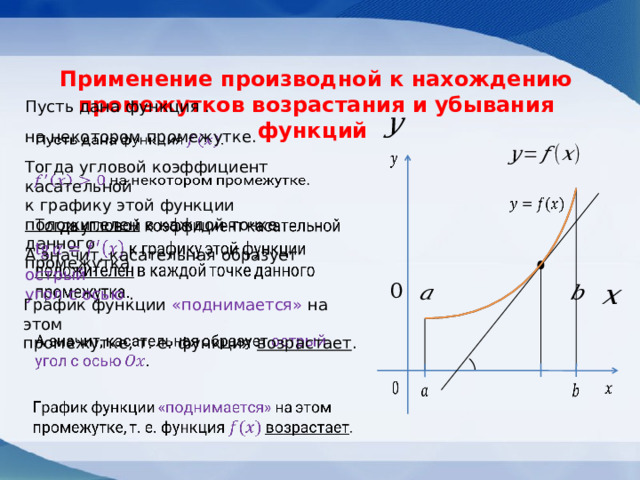
Применение производной к нахождению

промежутков возрастания и убывания функций

Пусть дана функция .

на некотором промежутке.

Тогда угловой коэффициент касательной

к графику этой функции

положителен в каждой точке данного

промежутка.

А значит, касательная образует острый

угол с осью .

График функции «поднимается» на этом

промежутке, т. е. функция возрастает .

Применение производной к нахождению

промежутков возрастания и убывания функций

Пусть дана функция .

Если на некотором промежутке,

то угловой коэффициенткасательной

к графику функции

отрицателен .

А значит, касательная образует тупой угол с осью .

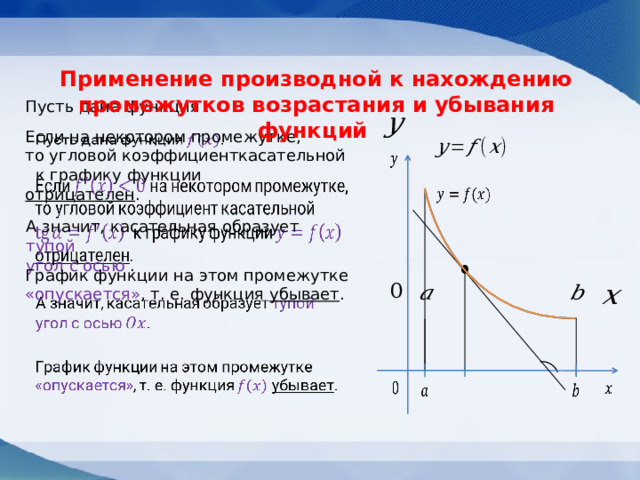
Применение производной к нахождению

промежутков возрастания и убывания функций

Пусть дана функция .

Если на некотором промежутке,

то угловой коэффициенткасательной

к графику функции

отрицателен .

А значит, касательная образует тупой

угол с осью .

График функции на этом промежутке

«опускается» , т. е. функция убывает .

Теорема Лагранжа

Если функция непрерывна на отрезке и дифференцируема

на интервале , то существует точкатакая, что

.

Теорему Лагранжа будем использовать при доказательстве теорем о достаточных условиях возрастания или убывания функции.

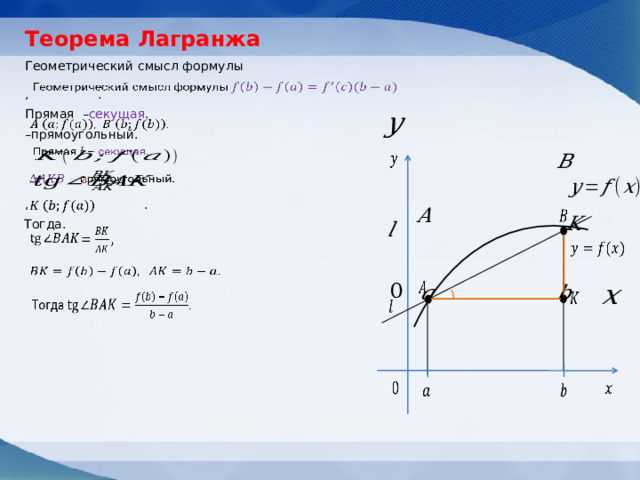
Теорема Лагранжа

Геометрический смысл формулы

.

,

Прямая – секущая .

– прямоугольный.

.

,

Тогда.

Теорема Лагранжа

Геометрический смысл формулы

,

.

Прямая – секущая .

– прямоугольный.

Угол равен углу наклона

между секущей и осью .

Теорема Лагранжа

Геометрический смысл формулы

.

,

Прямая – секущая .

– прямоугольный.

Угловой коэффициент секущей равен .

к графику функции в точке с абсциссой .

Получается, что на интервале найдётся такая точка ,

что в точке графика с абсциссой касательная к графику

функции параллельна секущей.

– угловой коэффициент касательной

Теорема о достаточном условии возрастания функции

Если функция дифференцируема на интервале и

для всех , то функция возрастает на интервале .

такие, что .

Пусть и – произвольные точки интервала ,

Доказательство:

Применим теорему Лагранжа к отрезку :

, .

, ;

т. к. .

,

Исследуем функцию на возрастание и убывание.

Область определения функции – множество.

.

Чтобы найти промежутки возрастания , надо решить неравенство ,

т. е. .

,

,

,

.

,

:

Исследуем функцию на возрастание и убывание.

Область определения функции – множество.

.

Чтобы найти промежутки возрастания , надо решить неравенство ,

т. е. .

,

,

,

.

,

и – интервалы возрастания функции .

Исследуем функцию на возрастание и убывание.

Область определения функции – множество.

.

Чтобы найти промежутки убывания функции, надо решить неравенство ,

т. е. .

,

,

,

.

,

– интервал убывания функции .

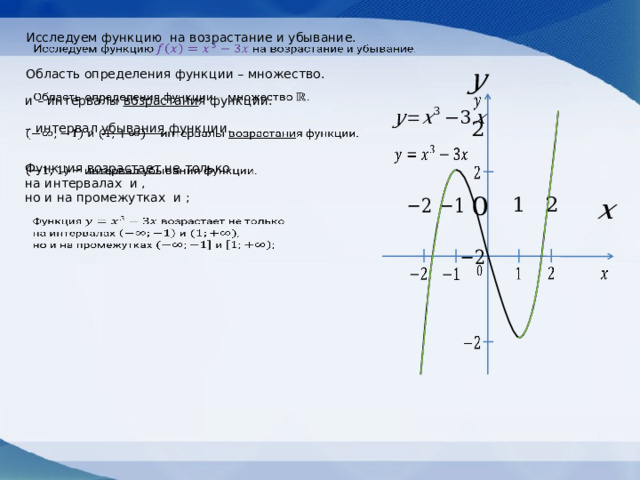
Исследуем функцию на возрастание и убывание.

Область определения функции – множество.

и – интервалы возрастани я функции.

– интервал убывания функции.

Функция возрастает не только

на интервалах и ,

но и на промежутках и ;

Исследуем функцию на возрастание и убывание.

Область определения функции – множество.

и – интервалы возрастани я функции.

– интервал убывания функции.

Функция возрастает не только

на интервалах и ,

но и на промежутках и ;

убывает не только на интервале ,

но и на отрезке .

Промежутки возрастания и убывания функции называют промежутками монотонности этой функции .

№ 900 (1,2)

№ 902 (1)

№ 909

ДОМАШНЕЕ ЗАДАНИЕ

• Прочитать § 49.
• Выполнить №900 (3,4,5,6); №902 (2,4); №904 (2); №908.