Презентация к уроку алгебры по теме "Функции, описывающие прямую пропорциональную зависимость, их графики" (8 класс)

Функции, описывающие прямую пропорциональную зависимость, их графики

Подготовила:

учитель математики

МБОУ Г.ГОРЛОВКИ «ШКОЛА № 42

Рыбина М.В.

Прямая пропорциональность

Функция вида у = kx , где х – аргумент, k – число – прямая пропорциональность.

k  0 k  0

Линейная функция

Функция вида у = kx + b , где х – аргумент, k и b – числа, называется линейной.

k  0 k  0

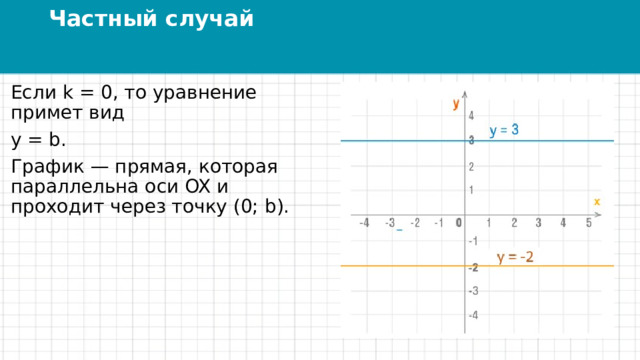
Частный случай

Если k = 0, то уравнение примет вид

y = b.

График — прямая, которая параллельна оси OX и проходит через точку (0; b).

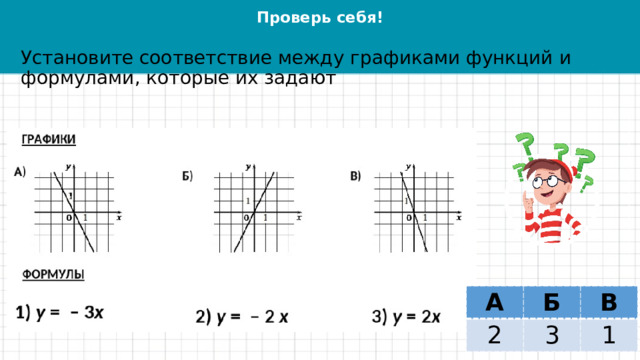
Проверь себя!

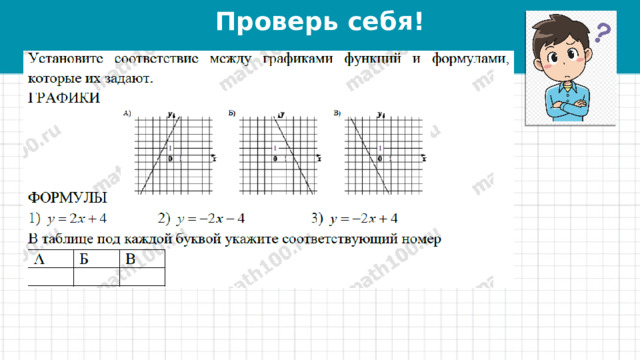
Установите соответствие между графиками функций и формулами, которые их задают

А

2

Б

В

3

1

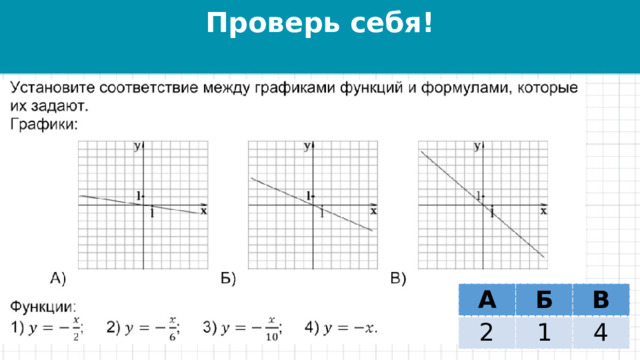
Проверь себя!

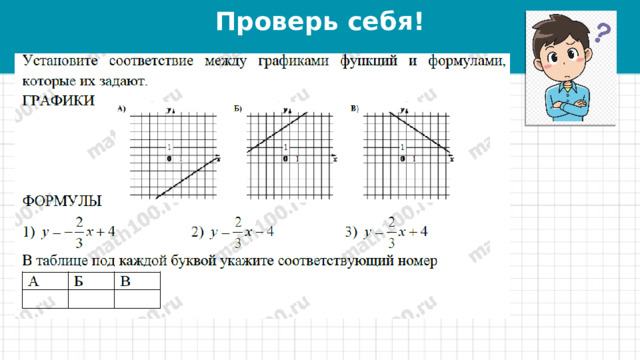
А

2

Б

В

1

4

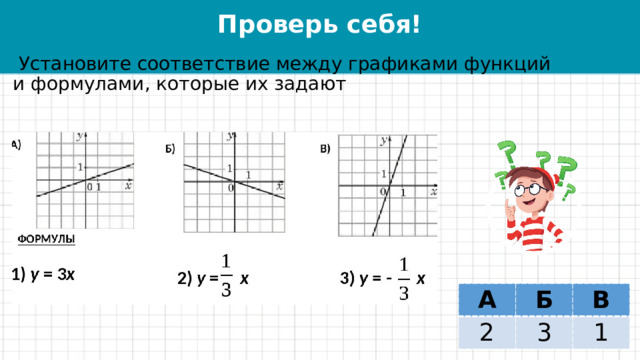
Проверь себя!

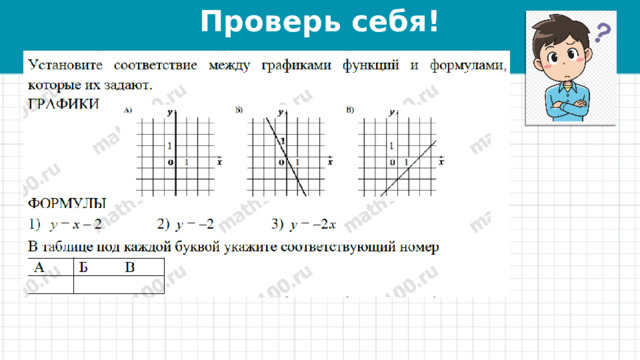
  Установите соответствие между графиками функций и формулами, которые их задают

А

2

Б

В

3

1

Проверь себя!

Проверь себя!

Проверь себя!

Проверь себя!

Проверь себя!

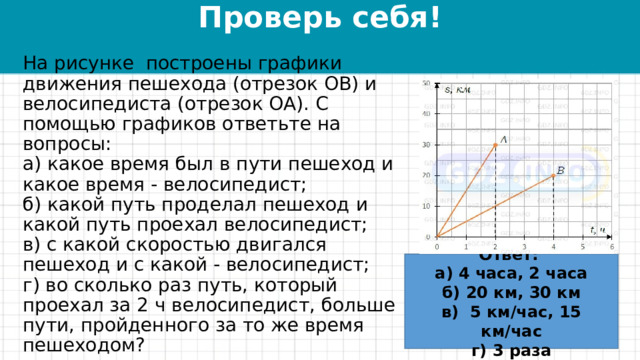
На рисунке построены графики движения пешехода (отрезок ОВ) и велосипедиста (отрезок ОА). С помощью графиков ответьте на вопросы: а) какое время был в пути пешеход и какое время - велосипедист; б) какой путь проделал пешеход и какой путь проехал велосипедист; в) с какой скоростью двигался пешеход и с какой - велосипедист; г) во сколько раз путь, который проехал за 2 ч велосипедист, больше пути, пройденного за то же время пешеходом?

Ответ:

а) 4 часа, 2 часа

б) 20 км, 30 км

в) 5 км/час, 15 км/час

г) 3 раза

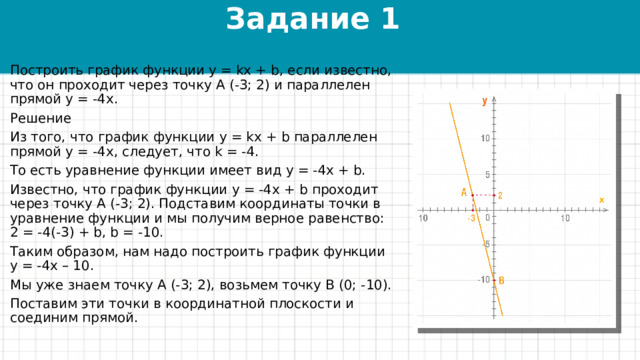
Задание 1

Построить график функции y = kx + b, если известно, что он проходит через точку А (-3; 2) и параллелен прямой y = -4x.

Решение

Из того, что график функции y = kx + b параллелен прямой y = -4x, следует, что k = -4.

То есть уравнение функции имеет вид y = -4x + b.

Известно, что график функции y = -4x + b проходит через точку А (-3; 2). Подставим координаты точки в уравнение функции и мы получим верное равенство: 2 = -4(-3) + b, b = -10.

Таким образом, нам надо построить график функции y = -4x – 10.

Мы уже знаем точку А (-3; 2), возьмем точку B (0; -10).

Поставим эти точки в координатной плоскости и соединим прямой.

Задание 2

Не выполняя построения, найдите координаты точек пересечения с осями координат графика функции у = -5х + 2

Решение

Пересечение с осью х: у = 0

-5х + 2 = 0, -5х = -2, х = 0,4

(0,4; 0)

Пересечение с осью у: х = 0

у = -5  0 +2=2

(0;2)

Ответ: (0,4; 0), (0; 2)

Задание 3

Найдите координаты точки пересечения графиков функций: у = -5х + 16 и у = 2х – 5.

Решение

-5х + 16 = 2х – 5,

-5х – 2х = -5 – 16,

-7х = -21,

х = 3

у = -5  3 + 16 = 1

Ответ: (3;1)

0, у " width="640"

Задание 4

Постройте график функции у = – 2 х – 4.

Укажите значение х , при которых у 0, у

Задание 5

Постройте график функции:

у = ;

Домашнее задание

• Каким должен быть коэффициент а уравнения ах – 4 у = 12, чтобы график этого уравнения проходил через точку А(10; 2)?
• При каком значении b график уравнения 6 х + bу = 0 проходит через точку А(2; 3)?
• Найдите значение k и b , если прямая у = kx + b проходит через точки А(5; 4) и В(– 10; 1).

4 . Найдите область определения функций

А) у = ;

Б) у = + ;

В) у = + ;