Презентация к уроку геометрии на тему "Понятие многогранника. Призма" (10 класс)

10 КЛАСС

ГЕОМЕТРИЯ

Понятие многогранника. Призма

Автор презентации: Попов Дмитрий Сергеевич

8 февраля

Дистанционное обучение

Тема: Понятие многогранника. Призма

Каждый из нас знаком с простейшими пространственными математическими фигурами – многогранниками. С некоторыми из них вы начали знакомиться еще в детстве, играя кубиками и собирая конструктор . Самая распространенная детская игрушка кубик дает нам первичные знания о кубе – один из видов правильных многогранников.

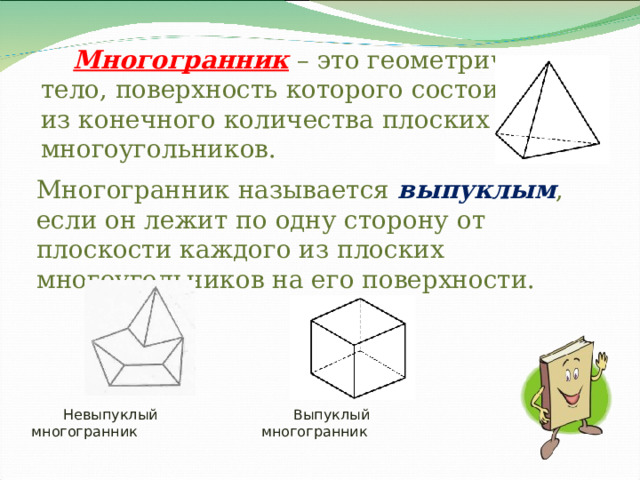
Многогранник – это геометрическое тело, поверхность которого состоит из конечного количества плоских многоугольников.

Многогранник называется выпуклым , если он лежит по одну сторону от плоскости каждого из плоских многоугольников на его поверхности.

Невыпуклый многогранник

Выпуклый многогранник

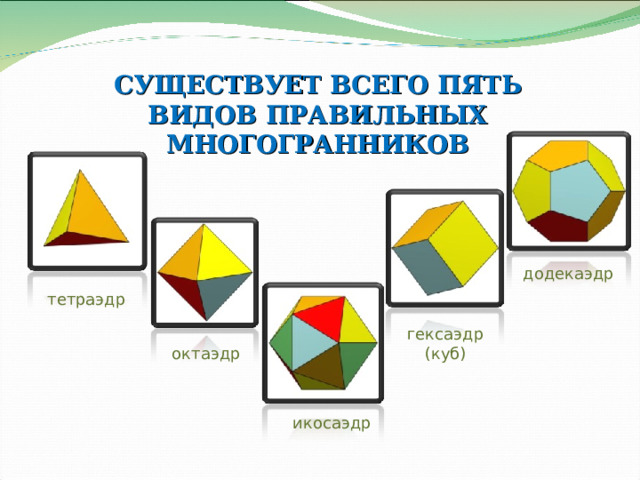
СУЩЕСТВУЕТ ВСЕГО ПЯТЬ ВИДОВ ПРАВИЛЬНЫХ МНОГОГРАННИКОВ

додекаэдр

тетраэдр

гексаэдр (куб)

октаэдр

икосаэдр

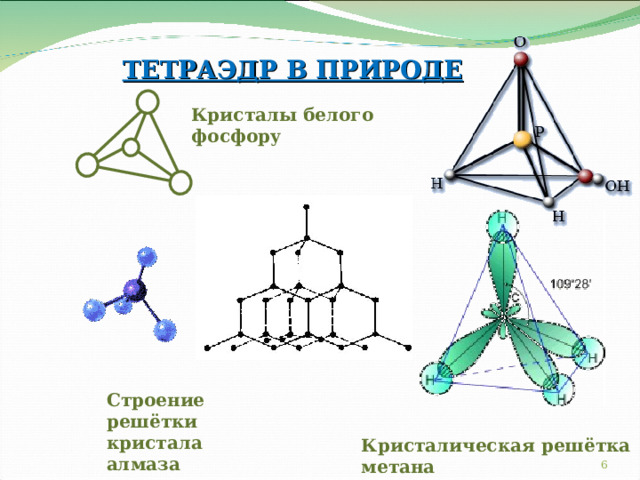
ТЕТРАЭДР В ПРИРОДЕ

Кристалы белого фосфору

Строение решётки кристала алмаза

Кристалическая решётка метана

ОКТАЭДР В ПРИРОДЕ

Углерод С характеризуется структурой октаэдра

Кристалы алмаза

6

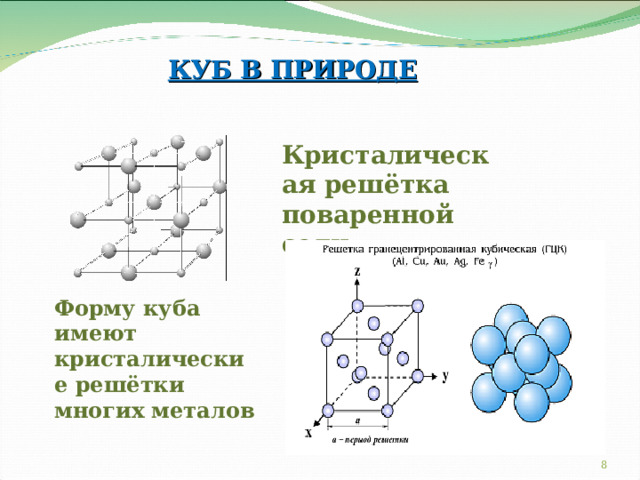
КУБ В ПРИРОДЕ

Кристалическая решётка поваренной соли

Форму куба имеют кристалические решётки многих металов

6

ИКОСАЭДР В ПРИРОДЕ

• Кристал бора имеет форму и коса э дра

• В биологии немецкий биолог начала ХХ века Эге Геккель исследовал, что одноклеточные организмы-феодарии, точно передают форму икосаэдра.

6

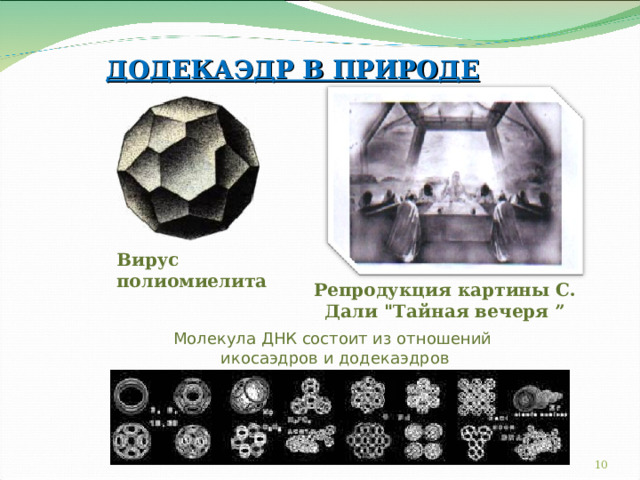
ДОДЕКАЭДР В ПРИРОДЕ

Вирус полиомиелита

Репродукция картины С. Дали "Тайная вечеря ”

Молекула ДНК состоит из отношений икосаэдров и додекаэдров

6

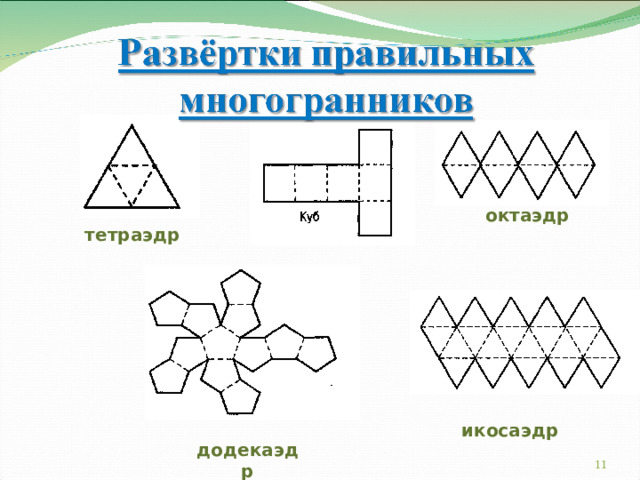
октаэдр

тетраэдр

икосаэдр

додекаэдр

6

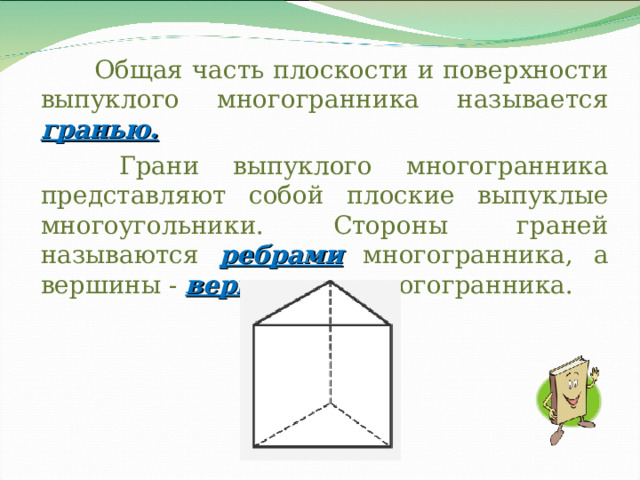
Общая часть плоскости и поверхности выпуклого многогранника называется гранью.

Грани выпуклого многогранника представляют собой плоские выпуклые многоугольники. Стороны граней называются ребрами многогранника, а вершины - вершинами многогранника.

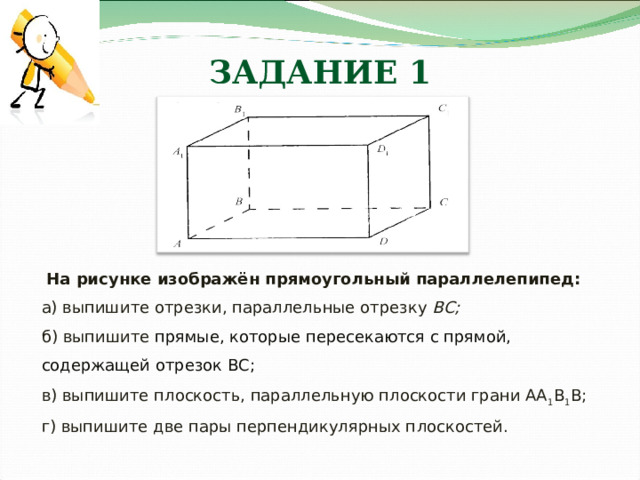
ЗАДАНИЕ 1

На рисунке изображён прямоугольный параллелепипед:

а) выпишите отрезки, параллельные отрезку ВС;

б) выпишите прямые, которые пересекаются с прямой, содержащей отрезок ВС;

в) выпишите плоскость, параллельную плоскости грани АА 1 В 1 В;

г) выпишите две пары перпендикулярных п лоскостей.

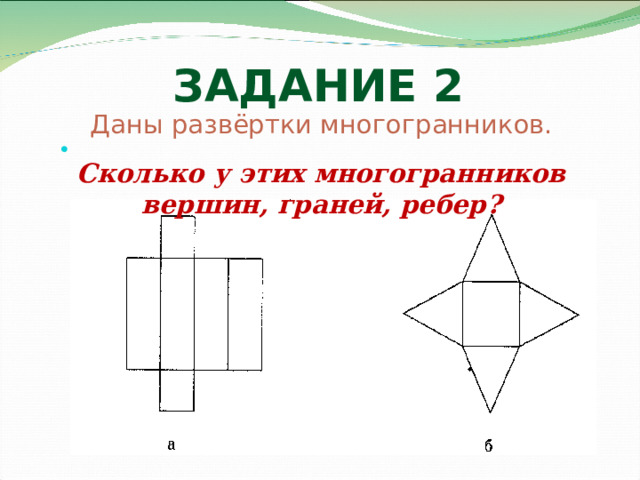
ЗАДАНИЕ 2

Даны развёртки многогранников.

Сколько у этих многогранников вершин, граней, ребер?

Призма

• Многогранник, у которого две грани– равны n -угольники с соответственно параллельными сторонами, а все остальные n граней –параллелограммы, называется n -угольной призмой.

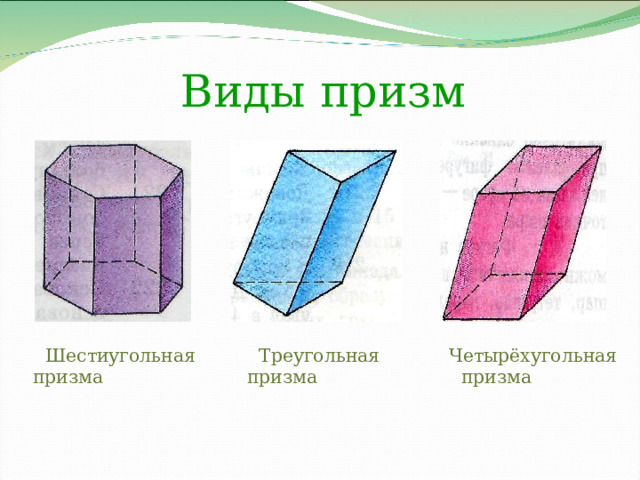
Виды призм

Шестиугольная Треугольная Четырёхугольная призма призма призма

Прямая и наклонная призмы

• Если боковые ребра призм перпендикулярны основанию, то призма называется прямой ,
• в другом случае – наклонной.
• Высота прямой призмы равна её боковому ребру.

Правильна призма

• Прямая призма называется правильной , если её основания – правильные многоугольники.
• В правильной призме все боковые грани – равные прямоугольники.

Правильные призмы

• Многоугольники A 1 A 2 …A n и B 1 B 2 …B n называются основаниями призмы ,

а параллелограммы – боковыми гранями призмы.

Боковые рёбра призмы

• отрезки A 1 B 1 , A 2 B 2 , … , A n B n называются боковыми рёбрами призмы

• Боковые ребра призм равны и параллельны.

Высота призмы

• Перпендикуляр, проведенный из какой-либо точки одного основания к плоскости другого основания, называется высотой призмы

Диагонали призмы

• Диагональю призмы называется отрезок, который соединяет две вершины призмы, не принадлежащих одной грани.

Диагональные сечения призм

• Сечение призмы плоскостью, которая проходит через два боковых ребра, которые не принадлежат одной грани, называется диагональным сечением

• Диагональные сечения призмы – параллелограммы .

Правила изображения призмы

• построить изображения оснований призмы;
• изобразить боковые рёбра в виде параллельных и равных отрезков;
• соединить последовательно их свободные концы.

• невидимые рёбра изображают штриховыми линиями.

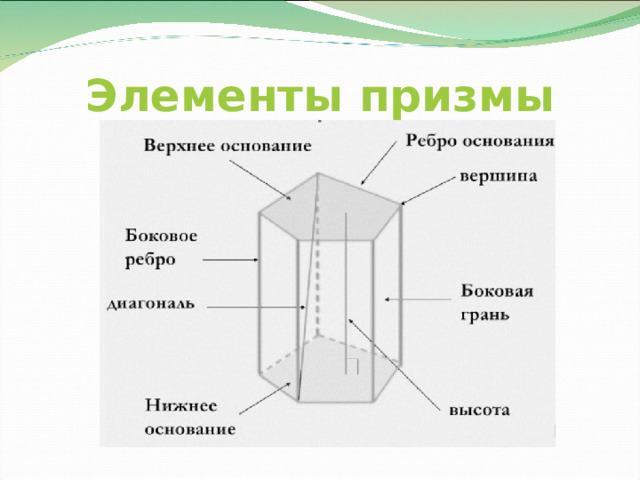
Элементы призмы

• Изучить п. 27, 30.
• Решите задачи:

• Основанием прямой треугольной призмы является прямоугольный треугольник с катетами 15 см и 20 см. Площадь большей боковой грани равна 75 см 2 . Вычисли высоту призмы.
• В правильной треугольной призме  ABCA 1 B 1 C 1  стороны оснований равны 2, боковые рёбра равны 5. Найдите площадь сечения призмы плоскостью, проходящей через середины рёбер  AB ,  AC ,  A 1 B 1  и  A 1 C 1 .