Россия, п.Солнцево Курской области
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 21.05.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 14.05.2025 19:35
Реброва Инна Борисовна
учитель физики и информатики
57 лет
8 482
5 237 
Местоположение
Специализация
Презентация к уроку информатики "Логические выражения и таблицы истинности".
Категория:
Информатика
08.02.2020 18:52
Просмотр содержимого документа
«Презентация к уроку информатики "Логические выражения и таблицы истинности".»
ЛОГИЧЕСКИЕ ВЫРАЖЕНИЯ И ТАБЛИЦЫ ИСТИННОСТИ
Логические выражения. Каждое составное высказывание можно выразить в виде формулы (логического выражения), в которую входят логические переменные , обозначающие высказывания, и знаки логических операций , обозначающие логические функции.
Запишем в форме логического выражения составное высказывание
«(2 · 2 = 5 или 2 · 2 = 4) и (2 · 2 ≠ 5 или 2 · 2 ≠ 4)»
Данное высказывание выглядит следующим образом:
А = « 2 · 2 = 5» - ложно (0)
В = « 2 · 2 = 4» - истинно (1)
Тогда составное высказывание выглядит:
«(А или В ) и (А или В) »
ЛОГИЧЕСКОЕ ВЫРАЖЕНИЕ
F = ( А v В) & (A v B).
Истинность или ложность составных высказываний можно определить чисто формально, руководствуясь законами алгебры высказываний, не обращаясь к смысловому содержанию высказываний.
F = ( А v В) & (A v B) = ( 0 v 1) & ( 1 v 0 ) = 1 & 1 = 1
ТАБЛИЦЫ ИСТИННОСТИ.
Для каждого составного высказывания (логического выражения) можно построить таблицу истинности, которая определяет его истинность или ложность при всех возможных комбинациях исходных значений простых высказываний (логических переменных).
При построении таблиц истинности целесообразно руководствоваться определенной последовательностью действий.
Во –первых, необходимо определить количество строк в таблице истинности. Оно равно количеству возможных комбинаций значений логических переменных, входящих в логическое выражение.
количество строк = 2 n
В нашем случае логическая функция
F = ( А v В) & (A v B) имеет 2 переменные и, следовательно количество строк в таблице истинности должно быть равно 4.
Во- вторых, необходимо определить количество столбцов в таблице истинности, которое равно количеству логических переменных плюс количество логических операций.
В нашем случае количество переменных равно двум, а количество логических операций – пяти, то есть количество столбцов таблицы истинности равно семи.
В – третьих, необходимо построить таблицу истинности с указанным количеством строк и столбцов, обозначить столбцы и внести в таблицу возможные наборы значений исходных логических переменных.
В- четвертых, необходимо заполнить таблицу истинности по столбцам, выполняя базовые логические операции в необходимой последовательности и в соответствии с их таблицами истинности.
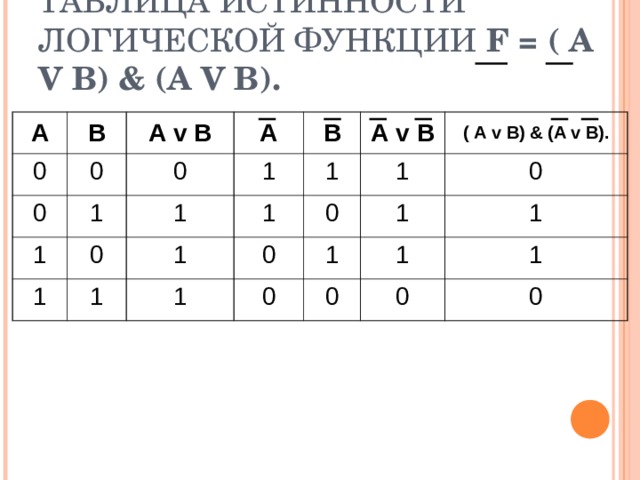
ТАБЛИЦА ИСТИННОСТИ ЛОГИЧЕСКОЙ ФУНКЦИИ F = ( А V В) & (A V B).
А
В
0
0
А v В
0
А
1
0
1
1
0
1
В
1
1
1
А v В
1
1
0
( А v В) & (A v B).
1
1
0
0
1
0
1
0
1
1
0
1
0
РАВНОСИЛЬНЫЕ ЛОГИЧЕСКИЕ ВЫРАЖЕНИЯ.
Логические выражения, у которых последние столбцы таблиц истинности совпадают, называются равносильными. Для обозначения равносильных логических выражений используется знак «=».
Докажем, что логические выражения А & B и A v B
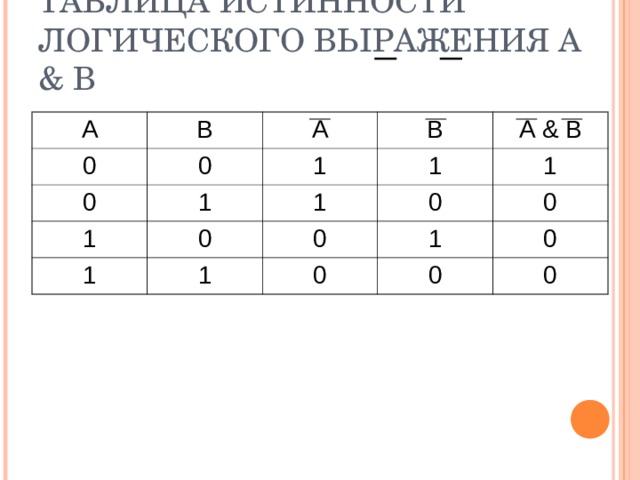
ТАБЛИЦА ИСТИННОСТИ ЛОГИЧЕСКОГО ВЫРАЖЕНИЯ A & B
А
В
0
0
А
0
1
В
1
1
0
1
А & В
1
1
1
0
0
1
0
0
1
0
0
0
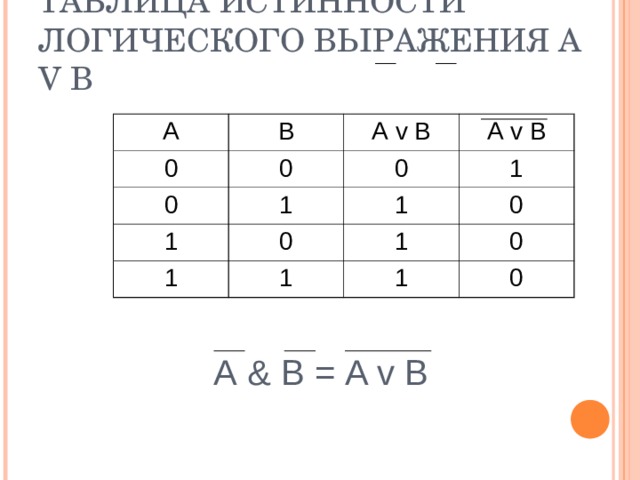
ТАБЛИЦА ИСТИННОСТИ ЛОГИЧЕСКОГО ВЫРАЖЕНИЯ A V B
А
В
0
0
0
А v В
0
1
1
А v В
0
1
1
1
1
1
0
0
1
0
А & В = A v B
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
Полезное для учителя
Реализация образовательных программ осуществляется с применением исключительно электронного обучения и ДОТ
