Презентация к уроку по теме "Сочетания и размещения"

Сочетания и размещения

Проверь себя

1 Вариант

2 вариант

• Достоверное событие- это событие, которое в результате опыта или наблюдения обязательно должно произойти. Вероятность такого события равна 1.
• А) 0,17

1.Невозможное событие - это событие, которое не может произойти в результате эксперимента.

Б) 0,475

Вероятность такого события равна 0.

В) 0,992

2. А) 0,11

Б) 0,25

В) 0,97

Найди ошибку

Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 бадминтонистов, среди которых 10 участников из России,  в том числе  Руслан Орлов. Найдите вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России?

10 * 1 = 1

26 10 26

Области применения комбинаторики:

• учебные заведения (составление расписаний);

• сфера общественного питания (составление меню);

• лингвистика (рассмотрение вариантов комбинаций букв).

• география (раскраска карт);

• спортивные соревнования (расчёт количества игр между участниками);

• производство (распределение нескольких видов работ между рабочими);

• агротехника (размещение посевов на нескольких полях);

• азартные игры (подсчёт частоты выигрышей);

• химия (анализ возможных связей между химическими элементами);

• биология (расшифровка кода ДНК);

• военное дело (расположение подразделений);

• астрология (анализ расположения планет и созвездий);

• экономика (анализ вариантов купли-продажи акций);

• криптография (разработка методов шифрования);

• доставка почты (рассмотрение вариантов пересылки).

• Первоначально комбинаторика возникла в XVI в. в связи с распространением различных азартных игр.

Перестановки

Размещения

Сочетания

Размещения – соединения, отличающиеся друг от друга составом элементов или их порядком, каждая из которых содержит k элементов, взятых из n различных элементов.

Порядок следования элементов важен.

Число размещений из n элементов по k обозначают

символом

(читается: А из n по k).

Перестановки

• Перестановкой множества из n   элементов называется расположение элементов в определенном порядке.

Число перестановок можно

вычислить по формуле P n =n!

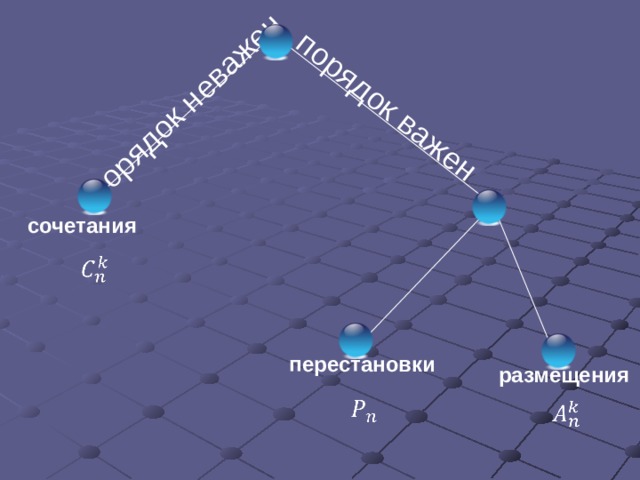
порядок важен

порядок неважен

сочетания

перестановки

размещения

Для любых натуральных чисел n и k,

таких, что k