Презентация на тему " Решение задач с параметром из ЕГЭ."

Решение задач с параметром из ЕГЭ

Выполнила ученица 11 класса А

Кудрявцева Маргарита Викторовна,

МАОУ "Лицей №14 имени Заслуженного учителя Российской Федерации

А.М. Кузьмина"

2018 учебный год

Актуальность темы

Актуальность данной темы определяется необходимостью уметь решать такие уравнения с параметрами при сдачи Единого Государственного экзамена и на вступительных экзаменах в высшие учебные заведения.

Цель и задачи

Цель: более глубокое изучение этой темы, выявление наиболее рационального решения, быстро приводящего к ответу.

Задачи:

1) дать определения понятию «уравнение с параметрами»;

2) показать принцип решения данных уравнений на общих случаях;

3) показать решение задач с параметром из ЕГЭ, используя различные методы;

4) составить алгоритм решения задач с параметром из ЕГЭ, с учетом формулировки задания;

5) систематизировать полученные данные в методическом пособии.

Прохожий спросил философа Сократа: — Сколько часов пути до города? Сократ ответил: — Иди… Путник пошел, и, когда он прошел двадцать шагов, Сократ крикнул: — Два часа! — Что же ты мне сразу не сказал? — возмутился тот. — А откуда я знал, с какой скоростью ты будешь идти?!

Что такое параметр?

Параметром называется независимая переменная, значение которой в задаче считается заданным фиксированным или произвольным действительным числом, или числом, принадлежащим заранее оговоренному множеству.

Особенность уравнений с параметрами: с одной стороны, параметр в уравнении следует считать величиной известной, а с другой — конкретное значение параметра не дано. С одной стороны, параметр является величиной постоянной, а с другой — может принимать различные значения. Получается, что параметр в уравнении — это «неизвестная величина», «переменная постоянная».

Что означает «решить задачу с параметром»?

Естественно, это зависит от вопроса в задаче. Если, например, требуется решить уравнение, неравенство, их систему или совокупность, то это означает предъявить обоснованный ответ либо для любого значения параметра, либо для значения параметра, принадлежащего заранее оговоренному множеству.

Если же требуется найти значения параметра, при которых множество решений уравнения, неравенства и т. д. удовлетворяет объявленному условию, то, очевидно, решение задачи и состоит в поиске указанных значений параметра.

Основные типы задач с параметрами

1. Уравнения, неравенства, их системы и совокупности, которые необходимо решить либо для любого значения параметра (параметров), либо для значений параметра, принадлежащих заранее оговоренному множеству.

2. Уравнения, неравенства, их системы и совокупности, для которых требуется определить количество решений в зависимости от значения параметра (параметров).

Основные типы задач с параметрами

3. Уравнения, неравенства, их системы и совокупности, для которых требуется найти все те значения параметра, при которых указанные уравнения, неравенства, их системы и совокупности имеют заданное число решений (в частности, не имеют или имеют бесконечное множество решений).

4. Уравнения, неравенства, их системы и совокупности, для которых при искомых значениях параметра множество решений удовлетворяет заданным условиям в области определения.

Основные способы (методы) решения задач с параметром

Всего есть 3 основных способа решения задач с параметром:

• Аналитический(способ так называемого прямого решения, повторяющего стандартные процедуры нахождения ответа в задачах без параметра);
• Графический(в зависимости от задачи(с переменной x и параметром a) рассматриваются графики или в координатной плоскости (x; y), или в координатной плоскости (x; a));
• Решение относительно параметра(при решении этим способом переменные x и a принимаются равноправными и выбирается та переменная, относительно которой аналитическое решение признается более простым. После естественных упрощений возвращаемся к исходному смыслу переменных x и a и заканчиваем решение).

x=2a при любом a ax=10 = x=10/a = x=10/a при a≠0 x=√a = x=√a при a≥0 2ax – 4=0 = 2ax=4 = x=2/a = x=2/a при a≠0 |x|= a –1 = a –1≥0 = x= a –1 или x=1–a при a≥1  " width="640"

Самые простые примеры

• x/2=a = x=2a при любом a
• ax=10 = x=10/a = x=10/a при a≠0
• x=√a = x=√a при a≥0
• 2ax – 4=0 = 2ax=4 = x=2/a = x=2/a при a≠0
• |x|= a –1 = a –1≥0 = x= a –1 или x=1–a при a≥1 

Разбор нескольких задач

1 задача: Для всех действительных значений параметра a решите уравнение  x 3 –(2–a)x 2 –ax–a(a–2)=0 .

Решение: Исходное кубическое по x уравнение является квадратным относительно  a . Поэтому, считая переменную  x  параметром, перепишем это уравнение в виде стандартного квадратного уравнения относительно a, опуская промежуточные шаги по раскрытию скобок и перегруппировке: –a 2 +(x 2 –x+2)a+x 3 –2x 2  = 0.

Преобразуем: a 2 –(x 2 –x+2)a –x 3  + 2x 2  = 0.

x 2 –x+2=x 2 +(2–x)

– x 3 +2x 2  =x 2 (2–x)

Легко заметить, что в первом случае можно увидеть сумму квадратов, а во втором их произведение. Поэтому по теореме, обратной теореме Виета получаем, что a 1 =x 2 , a 2 =2–x.

Исходное уравнение преобразуется в совокупность из двух: a=x 2  и a=2–x.

0 решений два, x=√a и x= – √a Второе уравнение совокупности будет иметь 1 корень при любом a. Мы смогли найти все решения исходного уравнения для любого действительного значения параметра: x=2–a при a x=0 или x=2 при a=0; x=√a или x=–√a   или x=2–a при a0. " width="640"

Из того, что x 2 =a следует, что:

1)при a

2)при a=0 решение будет всего одно, x=0

3)при a0 решений два, x=√a и x= – √a

Второе уравнение совокупности будет иметь 1 корень при любом a.

Мы смогли найти все решения исходного уравнения для любого действительного значения параметра: x=2–a при a

x=0 или x=2 при a=0; x=√a или x=–√a  

или x=2–a при a0.

Можно увидеть, что при a=1 равенства x=2–a и x=√a принимают одинаковое значение x=1. Можно легко найти второй такой корень, приравняв x=2 – a и x= – √a. Это будет x=–2 при a=4. Таким образом мы можем переписать ответ в более правильном виде: x=2–a  при  a 1 =0,

  x 2 =2  при  a=0; x=√a, x=–√a и x=2–x при 04; x=1, x=–1 при a=1; x=2, x=–2 при a=4.

2 задача: При каких a уравнение  |x 2 +2x–3|– –2a=|x–a|+3  имеет ровно три корня?

Решение: Используем графический метод решения. График функции  y=|x 2 +2x–3| отличается от параболы  y=x 2 +2x–3  только тем, что отрицательная ее область зеркально отражается вверх относительно оси  OX  (ведь модуль не может принимать отрицательных значений).

График функции  y= |x–a|+2a+3  представляет собой всем известную «галочку», вершина которой смещена в точку (a;2a+3).

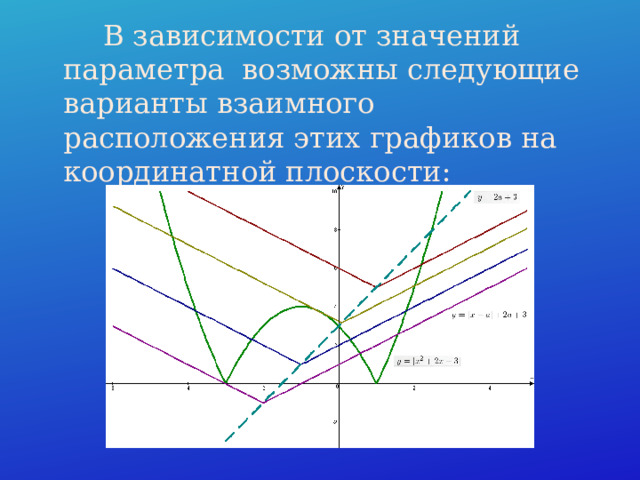
В зависимости от значений параметра  возможны следующие варианты взаимного расположения этих графиков на координатной плоскости:

Видно, что три решения уравнение будет в случае фиолетовой и бежевой «галочки». Первый случай выполняется при условии выполнения равенства  0=|–3–a|+2a+3, следовательно a=–2 .

Второй случай выполняется при условии, что дискриминант квадратного уравнения x 2 +x+3a=0 равен нулю, то есть при  a=1/12 .

Таким образом получается, что ответ на вопрос при каких a данное уравнение имеет ровно три корня такой: при a=–2 и a=1/12 .

0 . Тогда наше уравнение будет иметь вид: t 2 -3*t+a-1=0 . Это уравнение будет иметь 1 корень в двух случаях: 1)Если дискриминант будет равен 0 2)Если дискриминант будет больше нуля, но один из корней будет отрицательным Рассмотрим эти случаи. D=9-4a+4=13-4a=0 Отсюда получаем a=13/4 – первый подходящий корень. " width="640"

3 задача: При каких значениях параметра  a  уравнение  5 2x -3*5 x +a-

-1=0  имеет единственный корень?

Решение: Сделаем замену 5 x =t, t0 . Тогда наше уравнение будет иметь вид: t 2 -3*t+a-1=0 . Это уравнение будет иметь 1 корень в двух случаях:

1)Если дискриминант будет равен 0

2)Если дискриминант будет больше нуля, но один из корней будет отрицательным

Рассмотрим эти случаи.

• D=9-4a+4=13-4a=0

Отсюда получаем a=13/4 – первый подходящий корень.

0 t=(3-√(13-4a))/2≤0 Возьмем первый корень положительным, а второй наоборот. В таком случае условие единственного ответа будет выполнено. Решая неравенство t=(3+√(13-4a))/20 получаем, что a . Значит в ответ нужно записать, что aЄ(-∞;1)U{13/4} " width="640"

2) D=13-4a

Тогда корни будут такие:

t=(3+√(13-4a))/20

t=(3-√(13-4a))/2≤0

Возьмем первый корень положительным, а второй наоборот. В таком случае условие единственного ответа будет выполнено.

Решая неравенство t=(3+√(13-4a))/20 получаем, что a . Значит в ответ нужно записать, что aЄ(-∞;1)U{13/4}

Параметр в ЕГЭ 2018 года

Чтобы решить задание 18 по математике профильного уровня нужно знать: 

Задание 18 в ЕГЭ подразделяется на несколько видов:

1) функции, зависящие от параметра;

2) уравнения с параметрами;

3) неравенства с параметрами;

4) системы и неравенства с параметрами.

Пусть задано уравнение  f(x; a) = 0 , которое следует решить относительно переменной  х , а произвольное действительное число обозначено буквой  а , то  f(x; a) = 0  – это уравнение с параметром  а .

Решить неравенство с параметром  - это значит исследовать каким будет решение неравенства для всех возможных значений параметра. 

Решить уравнение с параметром – это значит найти все значения параметров, при которых данное уравнение имеет решение.

Линейные уравнения с параметрами

Линейные уравнения с параметрами —  общий вид   ax = b ,где  a , b – параметры.

Обратите внимание : для данного вида уравнения контрольным значением параметра является то значение, при котором обращается в нуль коэффициент при неизвестном.

При решении линейного уравнения с параметром рассматриваются случаи, когда параметр равен своему особому значению и отличен от него.

Особым значением параметра  а  является значение  а=0 . 

1)Если  а≠0 , то при любой паре параметров  а  и  b  оно 

имеет единственное решение .

2)Если  а=0 , то уравнение принимает вид  0х=b . В этом случает значение  b=0  является особым значением параметра  b .

3)При  b≠0 уравнение решений не имеет.

4)При  b=0  уравнение примет вид: 0х=0 . Решением данного уравнения является любое действительное число.

Дробно-рациональные уравнения с параметрами, сводящиеся к линейным.

Дробно-рациональные уравнения с параметрами, сводящиеся к линейным. При решении данного типа уравнений следует дробное уравнение заменить целым путем умножения обеих частей уравнения на общий знаменатель левой и правой его частей. Далее следует решать уравнение по известному алгоритму, исключив посторонние корни, т. е. те числа, которые обращают общий знаменатель в ноль (решить уравнения относительно параметра).  

0 ,  b 0 . ОДЗ такого уравнения находится как пересечение  областей допустимых значений функций  f(x)  и  φ(х) .  Для решения уравнения (1) нужно рассмотреть  следующие случаи: 1)При  a=b=1  решением уравнения (1) является область его допустимых значений  D . " width="640"

Показательные уравнения с параметрами

Показательные уравнения с параметрами

Многие показательные уравнения с параметрами сводятся к элементарным показательным уравнениям вида  а f (x)  = b φ(х)  (1), где  а 0 ,  b 0 .

ОДЗ такого уравнения находится как пересечение 

областей допустимых значений функций  f(x)  и  φ(х) . 

Для решения уравнения (1) нужно рассмотреть 

следующие случаи:

1)При  a=b=1  решением уравнения (1) является область его допустимых значений  D .

0 , a≠1 , b0 , b≠1 ) уравнение (1) равносильно уравнению f(x)=φ(х)  на области  D . 5)При  a≠b ( a0 , a≠1 , b0 , b≠1 ) уравнение (1) тождественно уравнению  на области  D . " width="640"

2)При  а=1 , b≠1  решением уравнения (1) служит решение уравнения  φ(х)=0  на области допустимых значений  D .

3)При  а≠1 , b=1  решением уравнения (1) служит решение уравнения  f(х)=0  на области допустимых значений  D .

4)При  a=b ( a0 , a≠1 , b0 , b≠1 ) уравнение (1) равносильно уравнению f(x)=φ(х)  на области  D .

5)При  a≠b ( a0 , a≠1 , b0 , b≠1 ) уравнение (1) тождественно уравнению  на области  D .

Выводы

Работа над данной темой была интересной и познавательной. Изучив методы решения уравнений с параметрами, я обогатила свой опыт:

• новыми научными понятиями;
• узнала методы, которые выходят за рамки школьной программы;
• углубила и расширила свои знания.

Выводы

Рассмотрев конкретные задачи, я пришла к выводу, что нужно уметь правильно видеть, какой метод решения подходит в той или иной ситуации, чтобы не тратить время, бесполезно решая задачу не тем способом. Именно это - научиться видеть, какой метод решения будет лучше в том или ином примере – является одной из целей проекта.

Выводы

Изучив данную тему, можем сделать вывод. Параметр – это буква, которая «никому ничем не обязана» и может принимать любые допустимые значения. Структура решений уравнения зависит от значений параметра; те или иные аспекты этой зависимости и предстоит выяснять в каждой конкретной задаче. Для этого нужно использовать различные формы и методы решения, с учетом свойств каждой конкретной функции.

Спасибо за внимание