Презентация на тему: "Теорема об отрезках пересекающихся хорд"

Теорема об отрезках

пересекающихся хорд

Геометрия, 8 класс

1. Закончите предложение:

1) Угол называется центральным, если …

2) Угол называется вписанным, если …

3) Центральный угол измеряется …

4) Вписанный угол измеряется …

5) Вписанные углы равны, если …

6) Вписанный угол, опирающийся на

полуокружность …

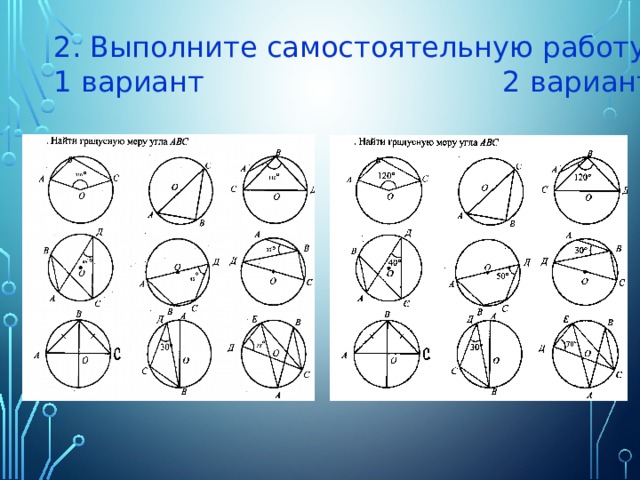
2. Выполните самостоятельную работу.

1 вариант 2 вариант

Практическая работа:

• Построить окружность с центром в точке О.
• Построить пересекающиеся хорды АВ и CD. Обозначить точку их пересечения.
• Измерить длины отрезков, на которые данная точка разделила эти хорды.
• Вычислить произведения отрезков каждой хорды.
• Сделать вывод.

АЕ∙ВЕ=СЕ∙DE. D " width="640"

Теорема Если две хорды окружности

пересекаются, то произведение отрезков одной

хорды равно произведению отрезков другой хорды.

Доказательство:

а)∆АСЕ~∆DВЕ(угол CAB равен углу CDB как вписанные углы, опирающиеся на дугу ВС;

угол АЕС равен углу DBE

как вертикальные).

C

А

E

B

б)

  =АЕ∙ВЕ=СЕ∙DE.

D

Решение задач.

• № 1. Хорды АВ и CD пересекаются в точке М. найдите длину хорды АВ, если АМ = 6 см, СМ = 8 см, МН = 9 см.
• № 2. Хорды КМ и РТ пересекаются в точке С. Найдите длину отрезков РС и СТ, если КС = 7 см, СМ = 4 см, РТ = 16 см.
• Решить № 666(а)

Домашнее задание.

• С.173 выучить с доказательством.
• № 666(б, в), 667.