Презентация по теме: "Математическое ожидание случайной величины, дисперсия и стандартное отклонение", Вероятность и статистика, 9 класс

Математическое ожидание случайной величины

Вероятность и статистика

9 класс

Повторение

В таблице дано распределение вероятностей некоторой случайной величины. Одна из вероятностей неизвестна. Найдите ее.

Значение Х

Вероятность

1

2

1/9

3

1/3

4

1/6

5

6

1/4

1/8

Ответ: 1/72

Математическое ожидание

Рассмотрим случайную величину Х и ее распределение

Значение Х

х1

Вероятность

p1

х2

p2

х3

p3

…

хn

…

pn

Если мы умножим значения случайной величины на их вероятности и сложим эти произведения, то получим некоторое среднее значение случайной величины.

Это среднее называют математическим ожиданием.

Обозначается математическое ожидание случайной величины Х, как ЕХ или Е(Х).

Математическое ожидание случайной величины – это сумма произведений значений этой величины и их вероятностей

ЕХ = х1*р1 + х2*р2 + х3*р3 + … + xn*pn

Говоря простым языком это «среднее значение» принимаемой случайной величины

Пример 1

Пусть случайная величина Х равна числу очков, выпавших на одной игральной кости. Вероятности выпадения каждой грани одинаковы и равны 1/6.

Поэтому:

ЕХ = 1*1/6 + 2*1/6 + 3*1/6 + 4*1/6 + 5*1/6 + 6*1/6 =(1+2+3+4+5+6)/6 = 7/2 = 3,5

Что нам это дает?

То, что кидая кость много (например 100) раз, в среднем каждый раз будет выпадать 3,5, а в сумме выпадет примерно 100*3,5=350.

Физический смысл математического ожидания

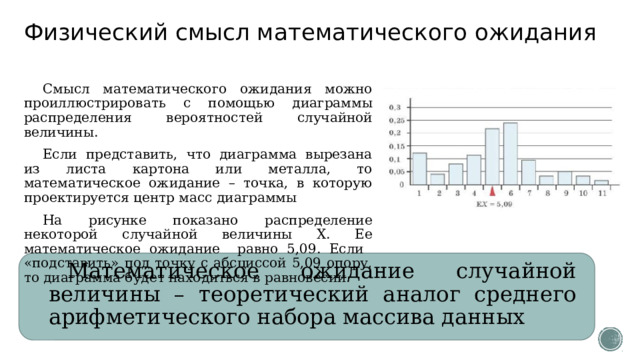
Смысл математического ожидания можно проиллюстрировать с помощью диаграммы распределения вероятностей случайной величины.

Если представить, что диаграмма вырезана из листа картона или металла, то математическое ожидание – точка, в которую проектируется центр масс диаграммы

На рисунке показано распределение некоторой случайной величины Х. Ее математическое ожидание равно 5,09. Если «подставить» под точку с абсциссой 5,09 опору, то диаграмма будет находиться в равновесии.

Математическое ожидание случайной величины – теоретический аналог среднего арифметического набора массива данных

Дисперсия и стандартное отклонение

Занимаясь описательной статистикой, мы говорили, что рассеивание значений измеряются с помощью дисперсии и стандартного отклонения.

В теории вероятности речь идет о случайных величинах. Для описания рассеивания случайной величины используются аналогичные характеристики: дисперсия и стандартное отклонение случайной величины.

Обозначают дисперсию случайной величины DX или D(X).

Дисперсией случайной величины Х называют математическое ожидание случайной величины (Х –ЕХ) 2 :

DX = Е(Х –ЕХ) 2

Случайная величина Х –ЕХ – это отклонение от среднего значения.

Значит дисперсия – это математическое ожидание квадрата отклонения случайной величины от своего математического ожидания.

Дисперсия и стандартное отклонение

Если дисперсия случайной величины мала, то мала вероятность того что случайная величина примет значение, значительно отличающиеся от математического ожидания

Если дисперсия равна нулю, то случайная величина Х принимает единственное значение. Это означает, что случайная величина постоянна.

Стандартным отклонением случайной величины Х называют квадратный корень из дисперсии:

Стандартное отклонение – это некоторое среднее типичное отклонение значений случайной величины от ее математического ожидания.

Работа в табличном процессоре Еxcel

Домашняя работа

§§70,71 на стр. 86-90 читать внимательно, рассмотреть все примеры.

№ 257, №266