Презентация по теме "Теория множеств", 9 класс

Понятие множества является одним из основных неопределяемых понятий математики и служит для описания совокупности предметов или объектов. Эти объекты, или элементы множества, считаются отличными друг от друга и от объектов не входящих в данное множество.

Множества  состоят из  элементов . Запись  x  M означает, что x является элементом множества M .

Задать множество, это значит указать способ с помощью которого можно сказать о любом объекте принадлежит он данному множеству или нет.

Выделяют два способа задания множеств:

1. Перечисление всех элементов множества

2. С помощью характеристического свойства

Характеристическое свойство – это свойство, которым обладает каждый элемент, принадлежащий множеству, и не обладает ни один элемент, который ему не принадлежит.

ПРИМЕР :

А – множество натуральных нечетных однозначных чисел.

А = {1,3,5,7,9}

В = {x  N: x≥5}

В = {5,6,7…}

N = {1, 2, 3, 4,…} – множество натуральных чисел;

Z = {…, -4, -3, -2, -1 , 0 , 1, 2, 3, 4,…} – множество целых чисел (содержит все натуральные числа и числа, им противоположные);

Q = {x ׀ х = p/q , где p ∈ Z, q ∈ N } – множество рациональных чисел (состоит из чисел, допускающих представление в виде дроби);

R = (- ∞ ; + ∞) – множество действительных чисел. Действительные числа изображаются точками координатной прямой (числовой оси).

Говорят, что множество B является подмножеством множества  A , если все элементы B являются элементами  A .

Это записывается так: В ⊂ А или

А ⊃ В . Говорят, что « В – подмноже-

ство А » или « В содержится в А »

или « А содержит В ».

Знак  называется знаком включения .

Если в множестве В найдется хотя бы один элемент, не принадлежащий множеству А , то В не является подмножеством множества А : В ⊄ А .

Заметим N ⊂ Z ⊂ Q ⊂ R .

1) ∅ ⊂ А для любого множества А ;

2) А  А для любого множества А (рефлексивность);

3) если А  В и В  А , то А = В (антисимметричность);

4) если А ⊂ В и В ⊂ С , то А ⊂ С (транзитивность).

РАВЕНСТВО МНОЖЕСТВ

Множества  A  и  B   равны  (запись: A=B ), если они содержат одни и те же элементы (другими словами, если A  B и  B  A ).

Пример: A={1,3,3,4}, B={4,3,1,  } , равны ли A и B ?

Да равны.

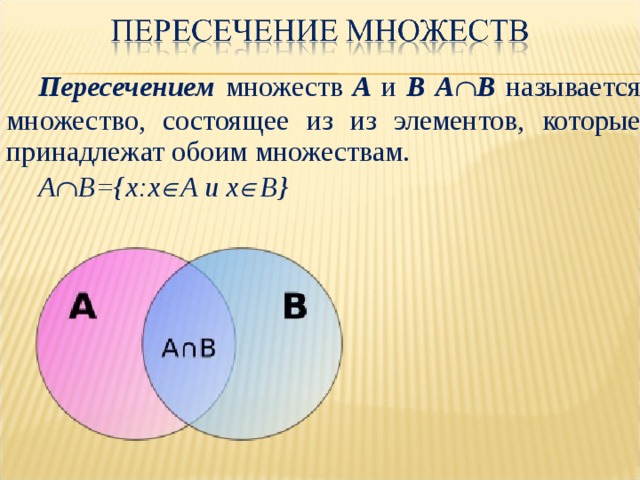
Пересечением множеств A и B А  В называется множество, состоящее из из элементов, которые принадлежат обоим множествам.

A  B={x:x  A и x  B}

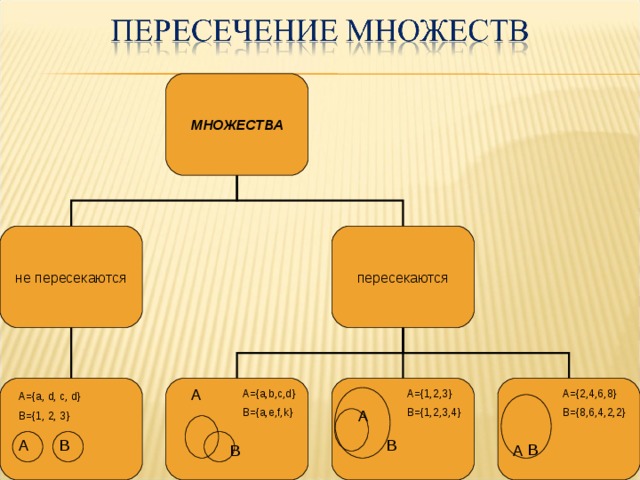
МНОЖЕСТВА

пересекаются

не пересекаются

A={1,2,3}

B={1,2,3,4}

A={a,b,c,d}

B={a,e,f,k}

A={2,4,6,8}

B={8,6,4,2,2}

А={a, d, c, d}

B={1, 2, 3}

А

В

В

В

В

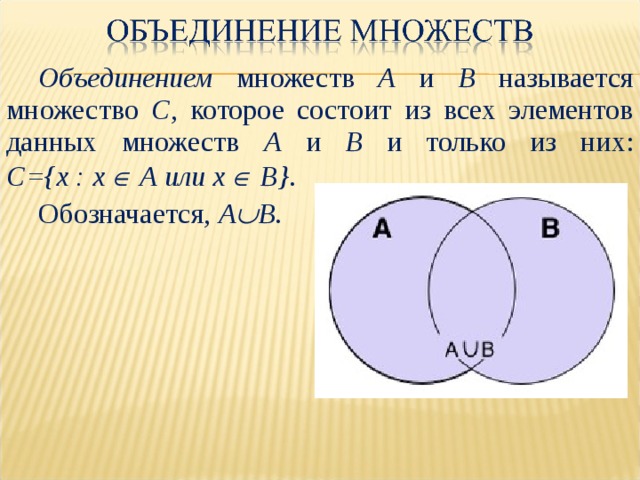
Объединением множеств А и В называется множество С , которое состоит из всех элементов данных множеств А и В и только из них: С={х : х  А или х  В} .

Обозначается, А  В .

Разностью множеств А и В называется множество С , состоящее из всех элементов множества А , не принадлежащих множеству В: С={х : х  А и х∉В} .

Обозначается, А\В .

В случае, когда В является подмножеством А , т.е. В ⊂ А , разность А\В называется дополнением множества В до множества А (или относительно множества А ).

1. коммутативность

5. существование 0

• A  B=B  A
• A  B=B  A

• A  = 
• A  =A

2. ассоциативность

7. законы поглощения

A  B 

• (A  B)  C=A  (B  C)
• (A  B)  C=A  (B  C)

• A  B=A
• A  B=B

3. дистрибутивность

• (A  B)  C=(A  C)  (B  C)
• (A  B)  C=(A  C)  (B  C)

Пары ( a i ,b i ) задают соответствие между множествами A и B , если указано правило R , по которому для элемента a множества A выбирается элемент b из множества B .

Пусть для некоторого элемента a множества A поставлен в соответствие некоторый элемент b из множества B , который называется образом элемента a и записывается b=R(a) . Тогда a=R -1 (b) - прообраз элемента b  B .

Образ множества A при соответствии R называется множеством значений этого соответствия и обозначается R(A) , если состоит из образов всех элементов множества А:

Прообраз множества B при некотором соответствии R называют областью определения этого соответствия и обозначают R -1 (B) т.е. R -1 является обратным соответствием для R .

Для описания соответствий между множествами используют понятие отображения .

Для задания отображения f необходимо указать:

1) множество, которое отображается ( область определения отображения, обозначается D(f) );

2) множество, в (на) которое отображается область определения ( множество значений этого отображения, обозначается E(f) );

3) закон или соответствие между этими множествами, по которому для элементов первого множества выбраны элементы из второго.

При записи f:A  B подразумевается, что отображение f определено всюду на A , т.е. A – полный прообраз отображения f, хотя для B такое свойство полноты не подразумевается.

Однозначным называется отображение, где каждому аргументу поставлено в соответствие не более одного образа. Такое отображение называется функцией .

Отображения можно задавать:

а) аналитически ( с помощью формул);

б) графически ( с помощью стрелочных схем);

в) с помощью таблиц.

Пусть множество А отображается взаимно-однозначно на множество В , т.е. f:A  B . Тогда отображение, при котором каждому элементу множества В ставится в соответствие его прообраз из множества А , называется обратным отображением для f и записывается f -1 :B  A .

Пусть A — множество. Множество всех подмножеств множества A называется булеаном A и обозначается  P(A) (2 A ) .

Справедливо следующее утверждение:

Число подмножеств конечного множества, состоящего из n элементов, равно 2 n .

Доказательство проведем методом математической индукции.

База . Если , т. е. множество пусто, то у него только одно подмножество — оно само ( 2  ={{  }}) , и интересующее нас число равно  2 0 =1 .

Индукционный шаг . Пусть утверждение справедливо для некоторого n и пусть  M  — множество у которого n +1 элементов. Зафиксировав некоторый элемент a , разделим подмножества множества  на два типа:

1) M 1 , содержащее  a ,

2) M 2 , не содержащее  a , то есть являющиеся подмножествами множества .

Подмножеств типа (2) по предположению индукции  2 n . Но подмножеств типа (1) ровно столько же, так как подмножество типа (1) получается из некоторого и притом единственного подмножества типа (2) добавлением элемента a и, следовательно, из каждого подмножества типа (2) получается этим способом одно и только одно подмножество типа (1).

Следовательно имеем  2 M =M 1  M 2  и  M 1  M 2 =  .