Презентация "Предмет стереометрии. Многогранники. 9 класс"

Предмет стереометрии. Многогранники

9 класс

Школьный курс геометрии состоит из двух частей:

• ПЛАНИМЕТРИИ

• СТЕРЕОМЕТРИИ

Планиметрия-это раздел геометрии, в котором изучаются свойства геометрических фигур на плоскости .

Стереометрия-это раздел геометрии, в котором изучаются свойства фигур

в пространстве .

Слово «стереометрия» происходит от греческих слов «стереос» - объемный, пространственный и «метрео» - измерять.

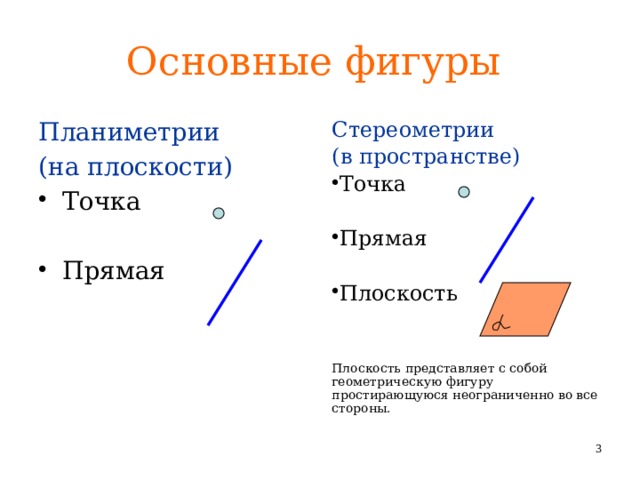
Основные фигуры

Стереометрии

Планиметрии

(на плоскости)

(в пространстве)

• Точка

• Точка

• Прямая

• Прямая

• Плоскость

Плоскость представляет с собой геометрическую фигуру простирающуюся неограниченно во все стороны.

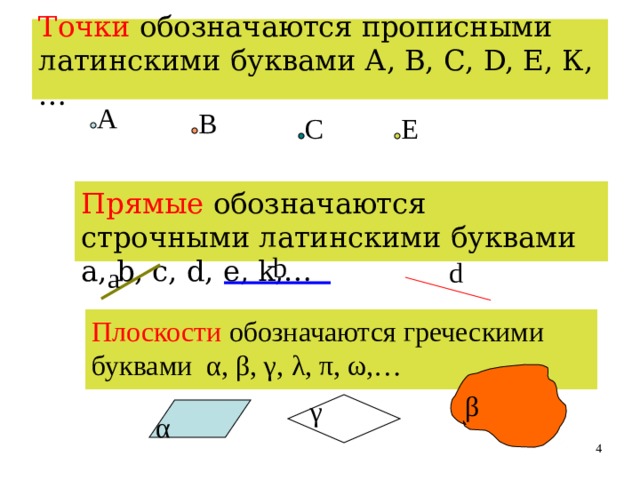
Точки обозначаются прописными латинскими буквами А, В, С, D, Е, К,…

А

В

С

Е

Прямые обозначаются строчными латинскими буквами a, b, c, d, e, k,…

b

d

a

Плоскости обозначаются греческими буквами α, β, γ, λ, π, ω,…

β

γ

α

Наряду с точками , прямыми , плоскостями в стереометрии рассматриваются геометрические тела , изучаются их свойства , вычисляются площади их поверхностей , а также вычисляются объёмы тел.

шар

цилиндр

куб

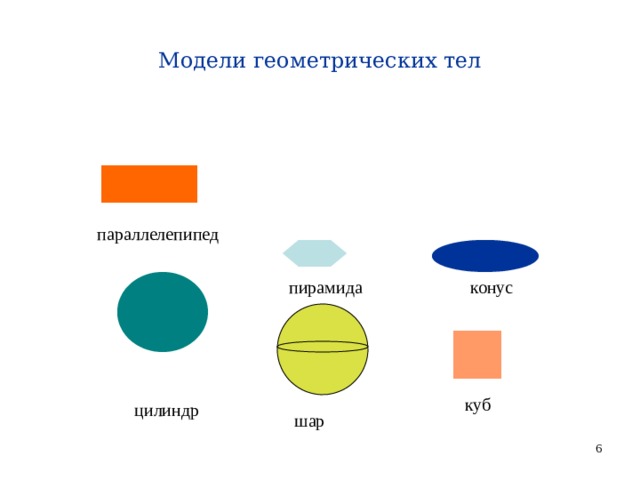
Модели геометрических тел

параллелепипед

пирамида

конус

куб

цилиндр

шар

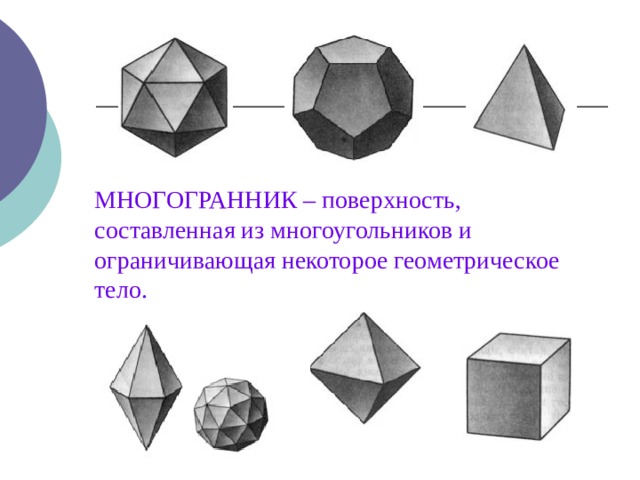
МНОГОГРАННИК – поверхность, составленная из многоугольников и ограничивающая некоторое геометрическое тело.

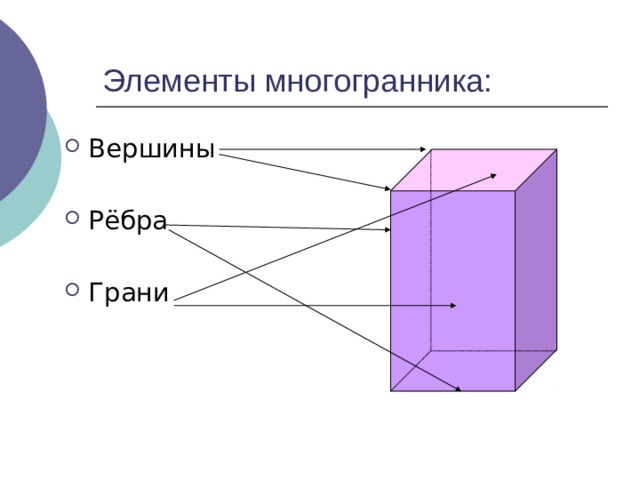
Элементы многогранника:

• Вершины

• Рёбра

• Грани

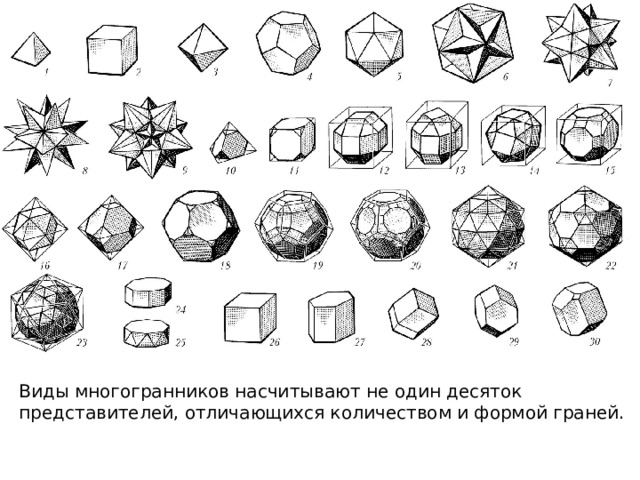
Виды многогранников насчитывают не один десяток представителей, отличающихся количеством и формой граней.

Многогранники делятся на :

• Выпуклые

Многогранник называется выпуклым, если он расположен по одну сторону от плоскости каждой его грани.

*Грани выпуклого многогранника являются выпуклыми многоугольниками ;

** В выпуклом многограннике сумма всех плоских углом при каждой его вершине меньше 360 0 .

• Невыпуклые

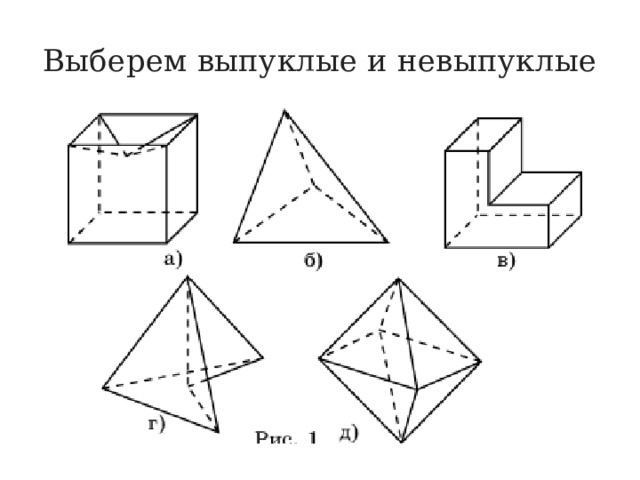
Выберем выпуклые и невыпуклые

Общие свойства многогранников:

Все они имеют 3 неотъемлемых компонента:

грани – многоугольники, из которых составлен многогранник;

ребра – стороны граней многогранника;

вершины – концы ребер.

Каждое ребро многоугольника соединяет две, и только две грани, которые по отношению друг к другу являются смежными.

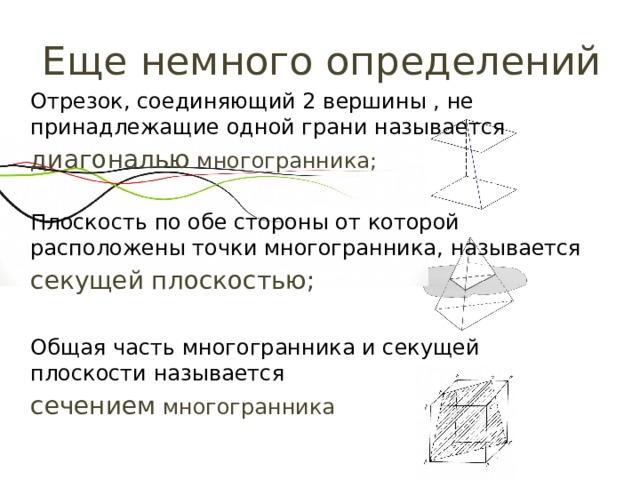
Еще немного определений

Отрезок, соединяющий 2 вершины , не принадлежащие одной грани называется

диагональю многогранника;

Плоскость по обе стороны от которой расположены точки многогранника, называется

секущей плоскостью;

Общая часть многогранника и секущей плоскости называется

сечением многогранника

Теорема Эйлера

Леонард Эйлер (1707 - 1783)

Th: В любом выпуклом многограннике сумма числа граней и числа вершин больше числа ребер на 2.

Г + В – Р = 2

Многогранники имеют красивые формы, например, правильные, полуправильные и звездчатые многогранники. Они обладают богатой историей, которая связана с именами таких ученых, как

Пифагор, Евклид, Архимед

• Букет Архимеда

• Букет Пуансо

• Букет Платона

Платоновы тела

Тетраэдр

Октаэдр

Гексаэдр

Додекаэдр

Икосаэдр

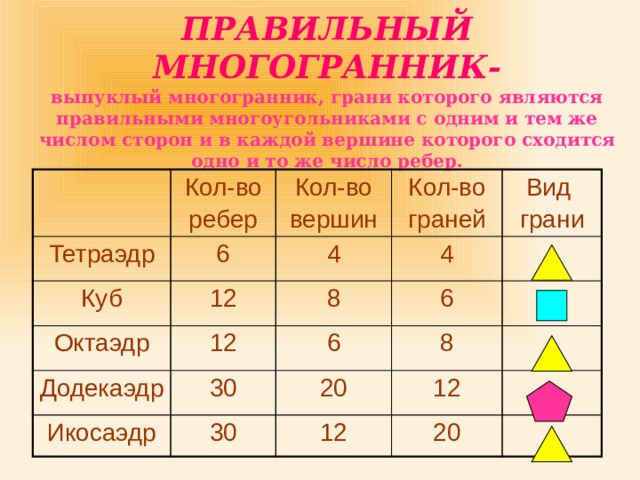
ПРАВИЛЬНЫЙ МНОГОГРАННИК- выпуклый многогранник, грани которого являются правильными многоугольниками с одним и тем же числом сторон и в каждой вершине которого сходится одно и то же число ребер.

Кол-во

Тетраэдр

ребер

6

Кол-во

Куб

вершин

Кол-во

12

Октаэдр

4

граней

12

4

Вид

8

Додекаэдр

30

6

грани

6

Икосаэдр

8

20

30

12

12

20

ТЕЛА АРХИМЕДА полуправильные однородные выпуклые многогранники

Архимедовыми телами называются выпуклые многогранники, все многогранные углы которых равны, а грани - правильные многоугольники нескольких типов (этим они отличаются от платоновых тел).

Множество архимедовых тел можно разбить на пять групп.

Первую группу составляют пять многогранников, которые получаются из пяти платоновых тел в результате их усечения:

усеченный тетраэдр,

усеченный куб,

усеченный октаэдр,

усеченный додекаэдр,

усеченный икосаэдр.

Вторую группу составляют два тела, называемых квазиправильными многогранниками. Это название означает, что гранями этого многогранника являются правильные многоугольники всего двух типов, причем каждая грань одного типа окружена гранями другого типа. Эти два тела называются

кубоктаэдр и

икосододекаэдр.

В третью группу входят

ромбокубоктаэдр,

который иногда называют малым

ромбокубоктаэдром и

ромбоикосододекаэдр ,

называемый также малым

ромбоикосододекаэдром .

В эту же группу входят

ромбоусеченный кубоктаэдр,

иногда называемый большим

ромбокубоктаэдром и ромбоусеченный

икосододекаэдр,

называемый также большим

ромбоикосододекаэдром , которые получаются

из кубоктаэдра и икосододекаэдра при другом

варианте усечения.

В четвертую группу входят две курносые модификации - курносый куб и курносый додекаэдр .

Для них характерно несколько повернутое положение граней. В результате эти многогранники, в отличие от предыдущих, не имеют плоскостей симметрии, но имеют оси симметрии. Так как плоскостей симметрии нет, то зеркальное отражение такого тела не совпадает с исходным телом, и поэтому существуют по две формы каждого из них - "правая" и "левая", отличающиеся так же, как правая и левая руки.

Тела

Кеплера - Пуансо

Среди невыпуклых однородных многогранников существуют аналоги платоновых тел - четыре правильных невыпуклых однородных многогранника или тела Кеплера - Пуансо.

Как следует из их названия, тела Кеплера-Пуансо - это невыпуклые однородные многогранники , все грани которых - одинаковые правильные многоугольники, и все многогранные углы которых равны. Грани при этом могут быть как выпуклыми, так и невыпуклыми.

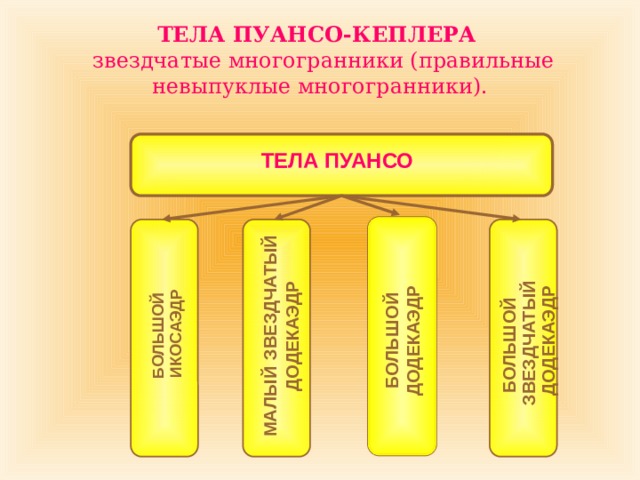
БОЛЬШОЙ

МАЛЫЙ ЗВЕЗДЧАТЫЙ ДОДЕКАЭДР

ИКОСАЭДР

БОЛЬШОЙ ДОДЕКАЭДР

БОЛЬШОЙ

ЗВЕЗДЧАТЫЙ

ДОДЕКАЭДР

ТЕЛА ПУАНСО-КЕПЛЕРА звездчатые многогранники (правильные невыпуклые многогранники).

ТЕЛА ПУАНСО

Большой звездчатый

Малый звездчатый

додекаэдр

додекаэдр

Звёздчатый октаэдр

Большой икосаэдр

25