
Прямая пропорциональность

Прямая пропорциональность
Определение . Прямой пропорциональностью называется функция вида у = kx , где k ≠ 0 – число.
у = 2х; у = -8х; у = 0,57х.
Естественная область определения прямой пропорциональности - вся числовая прямая.
Прямая пропорциональность имеет единственный нуль – это точка х = 0 .
Переменная у называется прямо пропорциональной переменной х (слово «прямо» часто опускается),
а число k – коэффициентом прямой пропорциональности .
Прямая пропорциональность
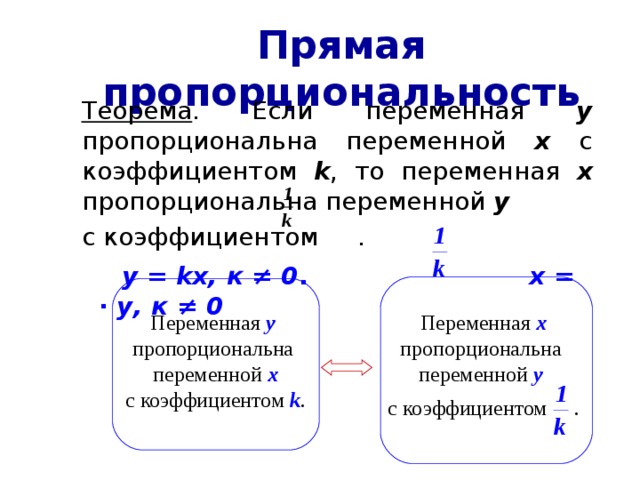
Теорема . Если переменная у пропорциональна переменной х с коэффициентом k , то переменная х пропорциональна переменной у
с коэффициентом .
у = k х, к ≠ 0 . х = ∙ у, к ≠ 0
Переменная у
пропорциональна
переменной х
c коэффициентом k .
Переменная х
пропорциональна
переменной у
c коэффициентом .

Прямая пропорциональность
Прямая пропорциональность переменных х и у означает, что их отношение постоянно, т.е. зависимость между ними при х ≠ 0
выражена формулой , k ≠ 0 .

Пример
Являются ли переменные p и q пропорциональными?
Решение .
p 1 : q 1 = 12,8 : 3,2 = 4 ; p 3 : q 3 = 20 : 5 = 4 ;
p 2 : q 2 = 16,4 : 4,1 = 4 ; p 4 : q 4 = 26,6 : 7,6 = 3,5 .
Ответ : Переменные p и q не пропорциональны .
q
3,2
p
12,8
4,1
5
16,4
20
7,6
8,4
26,6
33,6

Прямая пропорциональность
Теорема . Пусть переменные х и у прямо пропорциональны. Тогда при х ≠ 0 для их соответствующих значений верно равенство
.
Пример . Переменные а и b прямо пропорциональны. Зная, что а 1 = 37 , а 2 = 11 , b 2 = 17 , найти b 1 .
Решение. Поскольку а и b прямо пропорциональны , то
и значит .
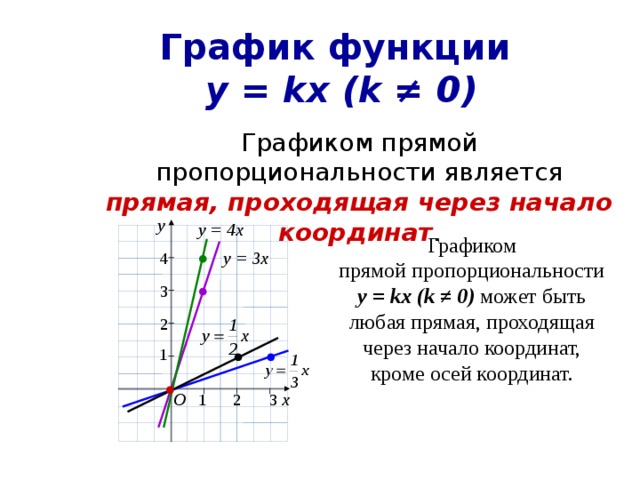
График функции у = kx (k ≠ 0)
Графиком прямой пропорциональности является прямая, проходящая через начало координат .
у
у = 4х
Графиком
прямой пропорциональности
у = kx (k ≠ 0) может быть
любая прямая, проходящая
через начало координат,
кроме осей координат.
у = 3х
4
3
2
1
О 1 2 3 х

Нечетная функция
Определение . Если значения функции, соответствующие любым двум противоположным значениям аргумента (т.е. значениям х и –х ), противоположны друг другу, то такая функция называется нечетной .
относительно нуля, т.е.
если х D( у), то и (-х) D( у).
График нечетной функции
симметричен относительно
начала координат О(0;0).
у
1
О 1 2 х
-2 -1
-1
у(-2) = - у(2) = -1.

Свойства функции у = kx (k ≠ 0)
Теорема (о свойствах функции у = kx , k ≠ 0 ).
- Областью определения функции у = kx (k ≠ 0) является множество R всех действительных чисел.
- Множеством значений функции у = kx (k ≠ 0 ) является множество R всех действительных чисел.
- Функция у = kx (k ≠ 0 ) не имеет ни наибольшего, ни наименьшего значений.
- График у = kx (k ≠ 0 ) имеет единственную точку пересечения с осями координат (0;0) – начало координат.
 0 , и убывающей, если k 0 . у k = - ½ k = ½ 0 у 1 1 О 1 2 х -2 -1 О 1 2 х -2 -1 -1 -1 Убывающая функция Возрастающая функция " width="640"
0 , и убывающей, если k 0 . у k = - ½ k = ½ 0 у 1 1 О 1 2 х -2 -1 О 1 2 х -2 -1 -1 -1 Убывающая функция Возрастающая функция " width="640"
Свойства функции у = kx (k ≠ 0)
- Значение аргумента х = 0 является нулем функции у = kx (k ≠ 0) .
- Функция у = kx (k ≠ 0) является нечетной.
- Функция у = kx (k ≠ 0) является возрастающей на области определения, если k 0 , и убывающей, если k 0 .
у
k = - ½
k = ½ 0
у
1
1
О 1 2 х
-2 -1
О 1 2 х
-2 -1
-1
-1
Убывающая функция
Возрастающая функция
 0) принимает отрицательные значения ( у ) при х (-∞; 0) и положительные значения ( у 0 ) при х (0; + ∞), т.е. ее график расположен в I и III координатных углах. Функция у = kx (k 0) принимает отрицательные значения ( у ) при х (0; + ∞) и положительные значения ( у 0 ) при х (-∞; 0), т.е. ее график расположен в II и IV координатных углах. k = ½ 0 k = - ½ у у I 1 1 II О 1 2 х -2 -1 -2 -1 -1 -1 III IV " width="640"
0) принимает отрицательные значения ( у ) при х (-∞; 0) и положительные значения ( у 0 ) при х (0; + ∞), т.е. ее график расположен в I и III координатных углах. Функция у = kx (k 0) принимает отрицательные значения ( у ) при х (0; + ∞) и положительные значения ( у 0 ) при х (-∞; 0), т.е. ее график расположен в II и IV координатных углах. k = ½ 0 k = - ½ у у I 1 1 II О 1 2 х -2 -1 -2 -1 -1 -1 III IV " width="640"
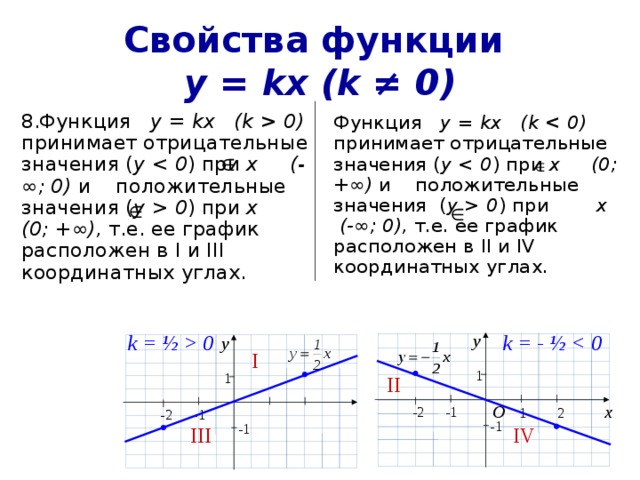
Свойства функции у = kx (k ≠ 0)
- Функция у = kx (k 0) принимает отрицательные значения ( у ) при х (-∞; 0) и положительные значения ( у 0 ) при х (0; + ∞), т.е. ее график расположен в I и III координатных углах.
Функция у = kx (k 0) принимает отрицательные значения ( у ) при х (0; + ∞) и положительные значения ( у 0 ) при х (-∞; 0), т.е. ее график расположен в II и IV координатных углах.
k = ½ 0
k = - ½
у
у
I
1
1
II
О 1 2 х
-2 -1
-2 -1
-1
-1
III
IV
















 0 , и убывающей, если k 0 . у k = - ½ k = ½ 0 у 1 1 О 1 2 х -2 -1 О 1 2 х -2 -1 -1 -1 Убывающая функция Возрастающая функция " width="640"
0 , и убывающей, если k 0 . у k = - ½ k = ½ 0 у 1 1 О 1 2 х -2 -1 О 1 2 х -2 -1 -1 -1 Убывающая функция Возрастающая функция " width="640"
 0) принимает отрицательные значения ( у ) при х (-∞; 0) и положительные значения ( у 0 ) при х (0; + ∞), т.е. ее график расположен в I и III координатных углах. Функция у = kx (k 0) принимает отрицательные значения ( у ) при х (0; + ∞) и положительные значения ( у 0 ) при х (-∞; 0), т.е. ее график расположен в II и IV координатных углах. k = ½ 0 k = - ½ у у I 1 1 II О 1 2 х -2 -1 -2 -1 -1 -1 III IV " width="640"
0) принимает отрицательные значения ( у ) при х (-∞; 0) и положительные значения ( у 0 ) при х (0; + ∞), т.е. ее график расположен в I и III координатных углах. Функция у = kx (k 0) принимает отрицательные значения ( у ) при х (0; + ∞) и положительные значения ( у 0 ) при х (-∞; 0), т.е. ее график расположен в II и IV координатных углах. k = ½ 0 k = - ½ у у I 1 1 II О 1 2 х -2 -1 -2 -1 -1 -1 III IV " width="640"




















