Презентация "Системы счисления", как дополнение к методике преподавания темы на уроках в 8-11 классах с углубленным изучением информатики и подготовки к ГИА.

Системы счисления

Учебная презентация по информатике

Автор: Звездина Вера Алексеевна,

учитель информатики

МБОУ «Образовательный центр №1»,

г.Ивантеевка Московской обл. 

Мысль выражать все числа немногими знаками,

придавая им, кроме значения по форме, еще

значение по месту, настолько проста, что

именно из-за этой простоты трудно понять,

насколько она удивительна. Как нелегко было

прийти к этому методу, мы видим на примере

высочайших гениев греческой культуры

Архимеда и Аполлония, от которых эта мысль

осталась скрытой.

Пьер-Симон Лаплас

Основные определения

Система счисления или нумерация – это способ записи (обозначения) чисел.

Символы, при помощи которых записываются числа, называются цифрами , а их совокупность – алфавитом системы счисления. Количество цифр, составляющих алфавит, называется его основанием ( размерностью ) .

Системы счисления

позиционные

непозиционные

десятичная, двоичная, восьмеричная, шестнадцатеричная и т.д.

древнеегипетская, древнерусская, римская

и т.д.

Заметим, что

цифровой ряд любой системы счисления начинается с нуля, а последняя цифра на единицу меньше ее основания.

Например:

в десятичной ‒ 0 1 2 3 4 5 6 7 8 9

в двоичной ‒ 0 1

в восьмеричной ‒ 0 1 2 3 4 5 6 7

Если основание системы счисления больше 10, то это правило также выполняется, но двузначные цифры при этом меняются на заглавные буквы латинского алфавита.

Например:

в одиннадцатеричной:

0 1 2 3 4 5 6 7 8 9 А

в шестнадцатеричной:

0 1 2 3 4 5 6 7 8 9 А B C D E F

Римская система счисления

• не является позиционной, т.к. каждый символ обозначает всегда одно и тоже число;

• цифры обозначаются латинскими буквами:

I, V, X, L, C, D, M

(1, 5, 10, 50, 100, 500, 1000)

Например: XXX – 30; XLI - 41

Позиционной называется система счисления ,

у которой количественный эквивалент цифры зависит от ее положения в записи числа .

Как и в привычной нам десятичной, в любой позиционной системе счисления значение числа образуется следующим образом: значения цифр умножаются на «веса» (степени основания) соответствующих разрядов и все полученные значения складываются.

Например, 3948 = 3*1000+9*100+4*10+8*1

1011 2 = 1*2 3 +0*2 2 +1*2 1 +1*2 0

Дружественными

(или родственными ) называются позиционные системы счисления, в основании которых лежит одно и то же число, но в разных степенях , причем «дружат» они через систему счисления с основанием в первой степени.

Например, двоичная, четверичная, восьмеричная, шестнадцатеричная и т.д. системы счисления «дружат» через двоичную, т.к. 2=2 1 , 4=2 2 , 8=2 3 , 16=2 4 и т.д.

Будем считать, что

десятичная система счисления не дружит ни с какой другой , так как ближайшая к ней сторичная система счисления в практических вычислениях нами не встречается.

Правила перевода между различными системами счисления делятся на две группы – между дружественными системами и нет.

Перевод между недружественными

системами счисления всегда выполняется через десятичную систему следующим образом:

1. Из десятичной системы счисления в любую – делением исходного числа на основание системы счисления, в которую переводим; при этом остатки от деления и последнее частное должны быть меньше этого основания. Частное и остатки от деления собираются справа налево.

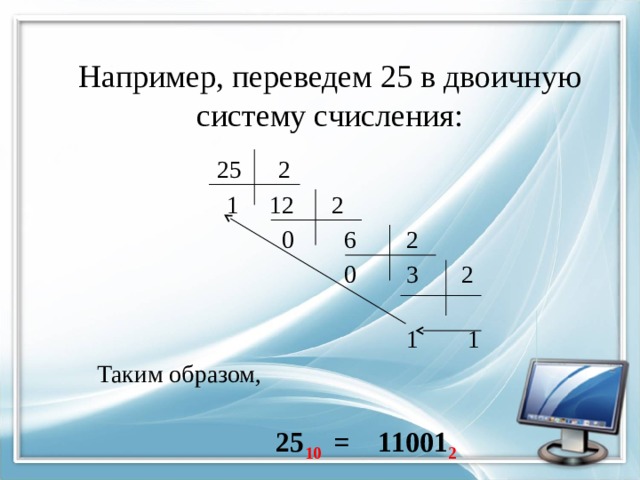
Например, переведем 25 в двоичную систему счисления:

25 2

1 12 2

0 6 2

0 3 2

1 1

Таким образом,

25 10 = 11001 2

Еще один (более простой, удобный и быстрый) способ перевода из десятичной в двоичную – это разложение исходного числа по степеням двойки следующим образом. Вычитаем из числа степень двойки, которая меньше числа, но максимально приближенную к нему. Затем с остатком проделываем те же действия до тех пор, пока не разложим все число.

Например:

25 = 16 + 8 + 1 = 2 4 + 2 3 + 2 0

(25 – 16 = 9 ; 9 = 8 + 1)

После этого, заменяем присутствующие степени двойки единицами, а пропущенные – нулями слева направо в порядке следования степеней, получая двоичную запись числа:

25 10 = 16 + 8 + 1 = 2 4 + 2 3 + 2 0 = 11001 2

Или:

651 10 = 512 + 128 + 8 + 2 + 1 =

= 2 9 + 2 7 + 2 3 + 2 1 + 2 0 = 1010001011 2

(651 – 512 = 139; 139 – 128 = 11; 11– 8 = 3 = 2 + 1)

Попробуйте выполнить эти переводы делением

и сравните время, потраченное на решение!

2. Для перевода из любой системы счисления в десятичную необходимо

представить исходное число в виде суммы степеней его основания и подсчитать десятичное значение этой суммы.

Например,

11001 2 =1*2 4 +1*2 3 +0*2 2 +0*2 1 +1*2 0 =25 10

Форма записи числа слева называется свернутой, а справа – развернутой.

Перевод между дружественными системами счисления

рассмотрим на примере перевода между двоичной, восьмеричной и шестнадцатеричной системами.

Для этого построим таблицу соответствия восьмеричных и шестнадцатеричных чисел двоичным , которую назовем таблицей «дружбы».

Левая часть этой таблицы включает цифры восьмеричной системы счисления, а правая дополняет ее для всех цифр шестнадцатеричной системы счисления).

Отметим, что так как каждая цифра в любой системе счисления занимает только одну позицию (один разряд числа), то в шестнадцатеричной системе счисления для записи цифр со значением больше 9 (здесь 11, 12, …, 15 – это цифры !) используют латинские заглавные буквы от A до F .

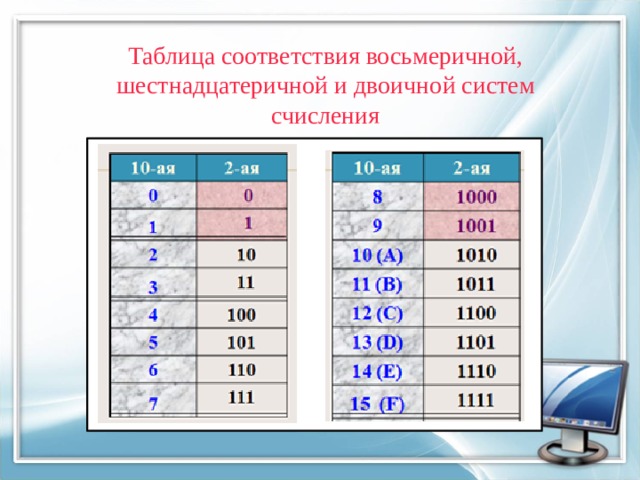
Таблица соответствия восьмеричной, шестнадцатеричной и двоичной систем счисления

Данная таблица разделена двойными линиями в местах условного ее деления на дружественные системы счисления ( двоичную, четверичную, восьмеричную и шестнадцатеричную ).

Отметим, что

длина чисел в двоичной системе счисления зависит от степени двойки в основании дружественной системы счисления , т.е. для записи цифр двоичной системы счисления достаточно одного разряда (т.к. 2 = 2 1 ), четверичной - два (4 = 2 2 ), восьмеричной (8 = 2 3 ), а шестнадцатеричной – четыре (16=2 4 ).

Именно это позволяет легко осуществлять перевод между дружественными системами счисления, записывая каждую цифру восьмеричного или шестнадцатеричного числа соответствующей ей в таблице двоичной цифрой с учетом того, чтобы длина двоичной цифры при этом строго соответствовала степени двойки основания исходной системы счисления.

Так как

8=2 3 , то меняем одну восьмеричную цифру на три двоичные - триады ;

16 = 2 4 , тогда меняем одну шестнадцатеричную цифру на четыре двоичные - тетрады ,

дополняя их при необходимости до нужной длины незначащими нулями слева .

Например,

152 8 = 001 101 010 2 = 1 101 010 2

1 5 2

(при этом первые два нуля не указываются, т.к. они незначащие),

152 16 = 0001 0101 0010 2 = 1 0101 0010 2

1 5 2

(при этом первые три нуля также

не указываются).

Перевод из восьмеричной системы счисления в шестнадцатеричную и обратно через двоичную систему счисления

выполняется перегруппировкой двоичных разрядов по четыре или по три во второй части выражений справа налево по количеству разрядов в степени результирующей системы счисления, а дальнейшая запись числа – как обычно, слева направо .

Н апример,

152 8 = 1 101 010 2 = 110 1010 2 = 6А 16

1 5 2 6 А

152 16 = 1 0101 0010 2 = 101 010 010 2 = 522 8

1 5 2 5 2 2

Группировка выполняется справа налево, потому что в случае, когда количество двоичных цифр не кратно трем (для перевода в восьмеричную систему счисления) или четырем (при переводе в шестнадцатеричную), тогда можно добавить нужное количество слева, т.е. незначащими нулями, не меняющими значения числа, а это произойдет, если приписать нули справа, где каждый добавленный ноль даст в результате умножение числа на 10.

Следует обратить внимание на несколько закономерностей , которые можно заметить в вышеприведенной таблице «дружбы» и аналогичных ей таблицах для других систем счисления, а так же легко проверить на десятичной системе счисления.

1. Любое основание N в своей

системе счисления выглядит

как 10 , т.е.

N 10 = 10 N

(т.е. 2 10 =10 2 – посмотрите в таблице,

8 10 =10 8, 16 10 =10 16 и т.д.).

2. Степень k любого основания N в своей системе счисления выглядит как единица и количество нулей, равных степени, т.е.

N k = 1 0…0 N

k

(посмотрите в таблице: 4=2 2 =100 2 ,

8=2 3 =1000 2 ,

тогда 16=2 4 =10000 2 ) и т.д.

3. Число, стоящее перед k -той степенью основания N, в своей системе счисления выглядит как последовательность из k самых больших цифр этой системы счисления, т.е.

N k – 1 = (N-1)…(N-1) N

k

тогда 2 k – 1 = 1…1 2

k

Посмотрите в таблице: 3=2 2 - 1=11 2 , 7=2 3 - 1=111 2 ,

15=2 4 - 1=1111 2 и т.д.

Аналогично в других системах счисления:

в восьмеричной :

8 k – 1 = 7…7 N

k

в десятичной :

10 k – 1 = 9…9 N

k

в шестнадцатеричной :

16 k – 1 = F…F N

k

4. Длина числа при переводе в любую систему счисления легко определяется по формуле:

N L -1 ≤ Ch L

где Ch – исходное число,

L - длина после перевода в систему счисления с

основанием N .

Например: 2 2 ≤ 5 3 , тогда при переводе в двоичную систему счисления длина числа будет равна 3, посмотрите в таблице: 5=101 2 ;

2 3 ≤ 13 4 , тогда при переводе в двоичную систему счисления длина числа будет равна 3, посмотрите в таблице: 13=1011 2

Если закономерности 1, 2 и 3 применяются для быстрого и точного перевода чисел между системами счисления , то закономерность 4 удобно использовать для первичной проверки правильности перевода чисел из десятичной системы счисления в любую другую , что позволит сэкономить время на проверке результата перевода и даст возможность

избежать ошибок .

Но использование закономерностей дает нам еще ряд преимуществ!

Одно из них (перевод из десятичной системы счисления в двоичную разложением десятичного числа по степеням двойки) уже рассмотрели выше. Заметим, что там применяются закономерности 1 и 2.

На чем еще можно сэкономить время и избежать ошибок?

Например, для перевода большого двоичного числа в десятичную систему счисления можно использовать в качестве промежуточной восьмеричную или шестнадцатеричную системы счисления:

110011101 2 = 110 011 101 2 = 635 8 =

=5*8 0 +3*8 1 +6*8 2 = 5 + 24 + 384 = 413

110011101 2 = 1 1001 1101 2 = 19D 16 =

=13*16 0 +9*16 1 +1*16 2 =

=13 + 144 + 256 = 413

Рассмотрим использование закономерностей при решении задач. Примечание. Так как любое число в нулевой степени равно единице, то при решении задач можно не писать степень в разряде единиц. 1. Переведите дво­ич­ное число 1110101 в де­ся­тич­ную систему счисления. Решение : 1110101 2 = 1 110 101 2 = 165 8 = =5+6*8 1 +1*8 2 =5+48+64=117 Или: 1110101 2 = 111 0101 2 = 75 16 = =5+7*16 1 =5+112=117 Ответ: 117

2. Переведите дво­ич­ное число 1100011 в

де­ся­тич­ную систему счисления.

Решение: 1100011 2 = 110 0011 2 = 73 16 =

=3+6*16 1 =3+96=99

Ответ : 99

3. Переведите число 125 из де­ся­тич­ной си­сте­мы счис­ле­ния в дво­ич­ную си­сте­му счисления. Сколь­ко еди­ниц со­дер­жит по­лу­чен­ное число? В от­ве­те ука­жи­те одно число —количество единиц .

Решение : 125 = 127 – 2 = 1111111 2 -10 2 =

= 1111101 2

Ответ : 5

 

4. Переведите число 135 из десятичной системы счисления в двоичную систему счисления. Сколько единиц содержит полученное число? В ответе укажите одно число —количество единиц . Решение: 135 = 128 + 4 + 2 + 1 ( = 2 7 + 2 2 + 2 1 + 2 0 ) Ответ : 4 Заметим, что этот ответ получен без окончательного перевода числа в двоичную систему счисления, достаточно посчитать количество двоек в степенях . Выражение в скобках можно не писать! Это позволяет сэкономить время решения задачи и избежать возможных ошибок при дальнейшей записи .

5. Переведите число FE из шест­на­дца­те­рич­ной си­сте­мы счис­ле­ния в дво­ич­ную си­сте­му счисления.   Решение : FE 16 = 1111 1110 2 (используем запись тетрадами из таблицы «дружбы»). Ответ : 11111110

6. Переведите число 143 из де­ся­тич­ной си­сте­мы счис­ле­ния в дво­ич­ную си­сте­му счисления. Сколь­ко зна­ча­щих нулей со­дер­жит по­лу­чен­ное число? В от­ве­те ука­жи­те одно число — ко­ли­че­ство нулей . Решение : 143 = 128+8+4+2+1 = 2 7 + 2 3 + 2 2 + 2 1 + 2 0 , то есть пропущены всего три (6,5 и 4) степени двойки. Ответ: 3  

7. Переведите число 305 из де­ся­тич­ной си­сте­мы счис­ле­ния в дво­ич­ную си­сте­му счисления. Сколь­ко еди­ниц со­дер­жит по­лу­чен­ное число? В от­ве­те ука­жи­те одно число — ко­ли­че­ство единиц . Решение : 305 = 256 + 32 + 16 + 1 (305 - 256 =49, 49 - 32 =17= 16 + 1 ) ( т.к. в сложении участвуют всего 4 степени двойки, то результат будет содержать всего 4 единицы. Степени можно даже не писать) Ответ : 4

8. Вычислите: 10101010 2  – 252 8  + 7 16 . Ответ запишите в десятичной системе счисления. Решение : Для решения задач такого типа нужно сначала перевести все числа в одну систему счисления, а уже потом выполнять действия между ними. Переведем первое число в восьмеричную систему счисления: 10101010 2 = 252 8 Тогда получаем выражение: 252 8  – 252 8  + 7 16 = 7 16 = 7 10 Отве т: 7

9. Вычислите значение выражения B9 16  − 271 8 . В ответе запишите вычисленное значение в десятичной системе счисления. Решение : Переведем первое число в восьмеричную систему счисления: В9 16 = 1011 1001 2 = 10 111 001 2 = 271 8 Тогда 271 8 − 271 8 = 0 Ответ : 0

10. Вычислите значение выражения EB 16  − 352 8 . Ответ запишите в десятичной системе счисления. Решение: Переведем первое число в восьмеричную систему счисления: EB 16 = 11101011 2 = 352 8 Тогда разница между двумя исходными числами равна 1. Ответ: 1

11. Укажите наименьшее четырёхзначное восьмеричное число, двоичная запись которого содержит 5 единиц. В ответе запишите только само восьмеричное число, основание системы счисления указывать не нужно. Решение : Наименьшее двоичное число, содержащее 5 единиц, равно 11111 2 . Но чтобы восьмеричное число было четырехзначным нужно, чтобы оно состояло из 4 триад (из 12 цифр). При этом первой цифрой двоичного числа обязательно должна быть 1 (два незначащих нуля в начале можно не писать), а остальные единицы будут занимать последние разряды числа. Тогда получаем: 00 1 000 001 111 2 = 1017 8 Ответ : 1017

12. Най­ди­те зна­че­ние вы­ра­же­ния 11 16  + 11 8  : 11 2 . Ответ за­пи­ши­те в дво­ич­ной си­сте­ме счис­ле­ния. Решение : В таких задачах, где нужно выполнять быстро и без ошибок вычисления в различных системах счисления, а результат требуется получить в десятичной, то и решение быстрее и проще выполнить в десятичной системе счисления. Поэтому переводим туда все исходные числа и считаем: 11 16 = 16+1 = 17 11 8 = 8+1 = 9 11 2 = 2+1 = 3 Тогда 17 + 9 : 3 = 20 20 = 16 + 4 = 2 4 + 2 2 = 10100 2 Ответ : 10100

13. Даны 4 целых числа, записанные в двоичной системе:   10001011, 10111000, 10011011, 10110100. Сколько среди них чисел, больших, чем A4 16 +20 8 ? Решение : Для выполнения действий над числами, представленными в разных системах счисления, нужно сначала перевести их в наиболее удобную для вас систему счисления, и только потом решать задачу. Для меня наиболее удобной является восьмеричная система счисления: 10001011 2 = 213 8 , 10111000 2 = 560 8 , 10011011 2 = 233 8 , 10110100 2 = 246 8 A4 16 = 10100100 2 = 244 8 , и 244 8 + 208 =264 8 . Из предложенных чисел подходит только второе число. Ответ : 1

14. Запись числа 69 10   в системе счисления с основанием N оканчивается на 1 и содержит 4 цифры. Чему равно основание этой системы счисления N? Решение : Для решения этой задачи используем две закономерности. Во-первых, последней цифрой числа при переводе из одной системы счисления в другую всегда является первый остаток от деления числа на основание системы счисления, куда переводим. Тогда искомое основание N должно быть кратно 68 (69=х*N+1, то х*N=68): 2, 4, 7 и т.д. Во-вторых, по закономерности 4, получаем N 3 ≤ 69 Ответ : 4

15. В системе счисления с основанием N запись числа 41 10  оканчивается на 2, а запись числа 131 10  — на 1. Чему равно число N? Решение : Т.к. в остатках чисел у нас есть цифры 2 и 1, то N≥3. При этом нужно найти число N, кратное числам 39 и 130. Следовательно, N = 13. Ответ : 13

16. В какой си­сте­ме счис­ле­ния вы­пол­ня­ет­ся ра­вен­ство 12 · 13 = 211? В от­ве­те ука­жи­те число – ос­но­ва­ние си­сте­мы счис­ле­ния. Решение : При переводе числа 211 N в десятичную систему счисления получаем уравнение: 211 N = 2*N 2 + 1*N +1 Для перевода множителей 12 и 13 в десятичную систему счисления вспомним закономерность 1. Тогда 12 N = N+2, 13 N = N+3. Следовательно, получаем уравнение: (N+2)(N+3) = 2*N 2 + N +1 Корнями данного уравнения являются 5 и -1. Но т.к. основание системы счисления является натуральным числом, то N = 5. Ответ : 5

17. Укажите наименьшее основание системы счисления, в которой запись числа 50 трехзначна. Решение : По закономерности 4 получаем N 2 ≤ 50 Ответ : 4

Вопросы, замечания или рекомендации по презентации или по теме в целом принимаются на сайте звездина.рус через форму обратной связи, в группе сайта Вконтакте или по электронной почте v_zvezdina@mail.ru