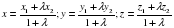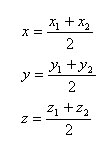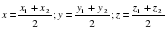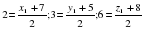Прямоугольная система координат в пространстве. Координаты середины отрезка. Расстояние между двумя точками.

Бурковская Нина Дмитриевна.

Уральский технологический колледж «Сервис», г.Уральск, ЗКО,РК

Преподаватель математики.

Тема программы: Координаты вектора в пространстве -12 часов.

Тема урока: Прямоугольная система координат в пространстве. Координаты середины отрезка. Расстояние между двумя точками.

Цель урок:

Образовательные: Рассмотреть понятие системы координат и координаты точки в пространстве; вывести формулу расстояния в координатах; вывести формулу координат середины отрезка.

Развивающие: Способствовать развитию пространственного воображения учащихся; способствовать выработке решения задач и развития логического мышления учащихся.

Воспитательные: Воспитание познавательной активности, чувства ответственности, культуры общения, культуры диалога.

Тип урока: Изучение новой темы, формирование зун.

Методы ведения: лекция

Оборудование урока Математическая среда GeoGebra чертежные принадлежности

ХОД УРОКА:

1. Организационный момент – 1 – 2 мин.

1. Приветствие учащихся.

2. Отметить отсутствующих.

II. Опрос по домашнему заданию

1.Какая система координат называется декартовой прямоугольной?

2. Что указывают координаты точки?

3. Чем определяется положение точки в координатной плоскости?

4 Чему равно расстояние от точки с заданными координатами до осей координат?

III. Объяснение нового материала. Краткий конспект.

В общеобразовательном курсе изучается прямоугольная система координат на плоскости и в пространстве. Иначе её называют Декартовой системой координат по имени французского ученого философа Рене Декарта (1596 – 1650) впервые введшего координаты в геометрию.

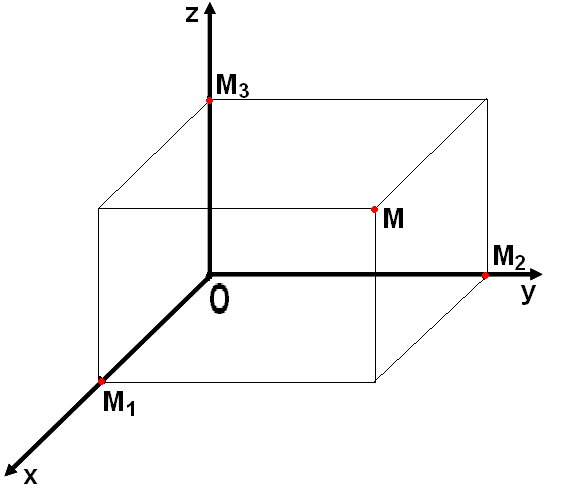
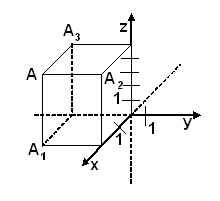
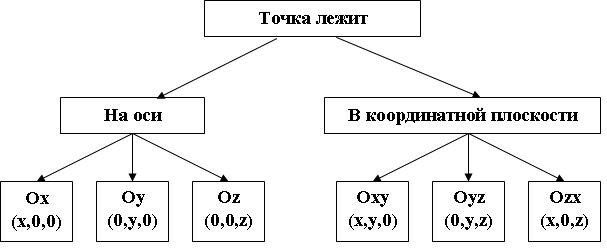
Три плоскости, проходящие через оси координат Ох и Оу, Оу и Оz, Оz и Ох, называются координатными плоскостями: Оху, Оуz, Оzх.

В прямоугольной системе координат каждой точке М пространства сопоставляется тройка чисел – её координаты.

М (х,у,z), где х – абсцисса, у – ордината, z - аппликата.

Расстояние между точками

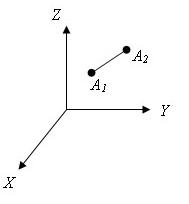
Есть две произвольные точки A₁(x₁;y₁;z₁) и A₂(x₂;y₂;z₂)

Тогда расстояние между точками A₁ и A₂ вычисляется так:

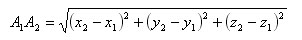
Пример 1:

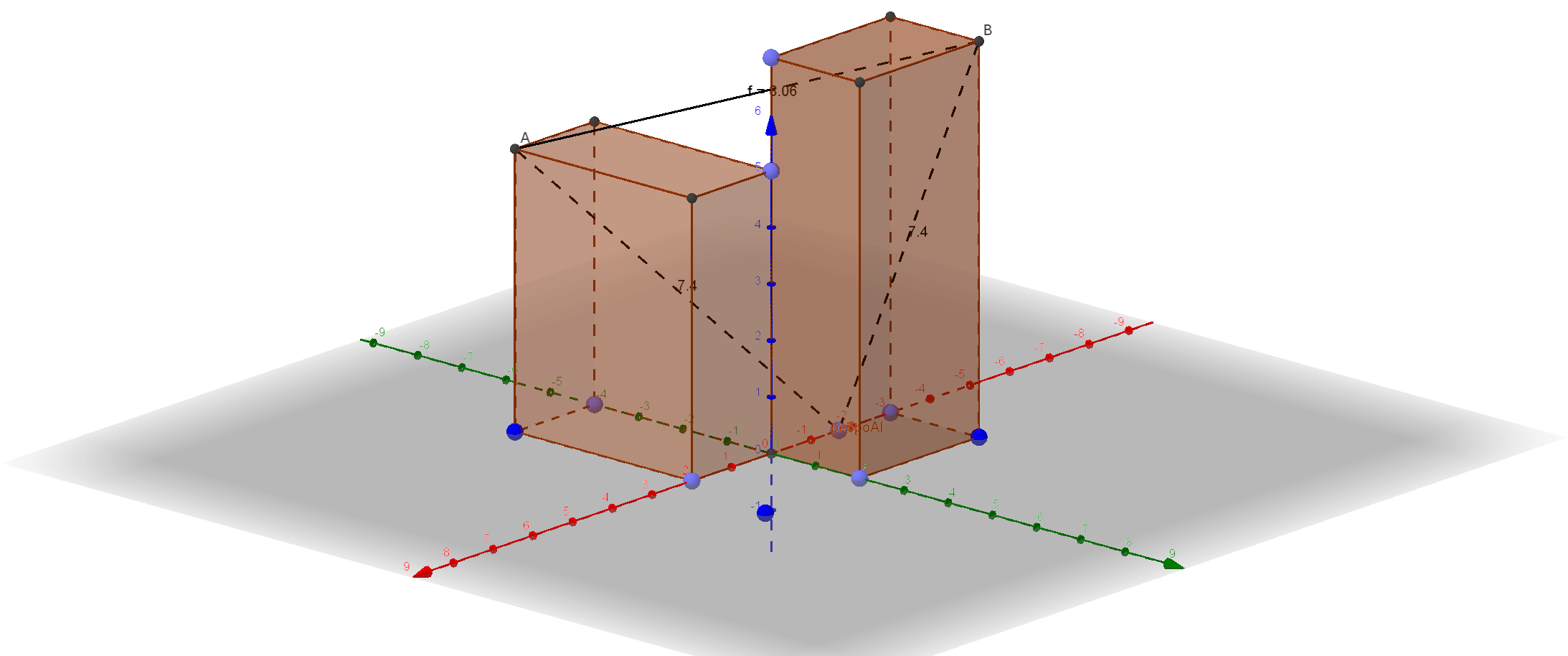
На оси ОХ найти точку, равноудалённую от точек А(2;-4;5) и В(-3;2;7).

Решение:

Пусть т. М – искомая точка. Так как т. М лежит на оси Ох, то она имеет координаты (х,0,0). По условию задачи .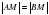

;.

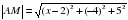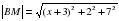Приравняем эти равенства и возведём в квадрат:

(х-2)²+41=(х+3)²+53. Решая это уравнение, получим:

10х=-17, х=-1,7. Значит координаты т.М будут (-1,7;0;0)

Ответ: М (-1,7;0;0)

Координаты точки С(х,у,z), делящий отрезок между точками М₁(х₁; y_1; z₁) и М₂(х₂; y_2; z₂) в заданном отношении λ определяется по формулам:

В частности, при λ=1 получаются формулы середины отрезка:

Координаты середины отрезка в пространстве

Есть две произвольные точки A₁(x₁;y₁;z₁) и A₂(x₂;y₂;z₂). Тогда серединой отрезка A₁A₂ будет точка Сс координатами x, y, z, где

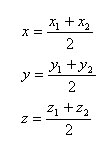
Пример 2:

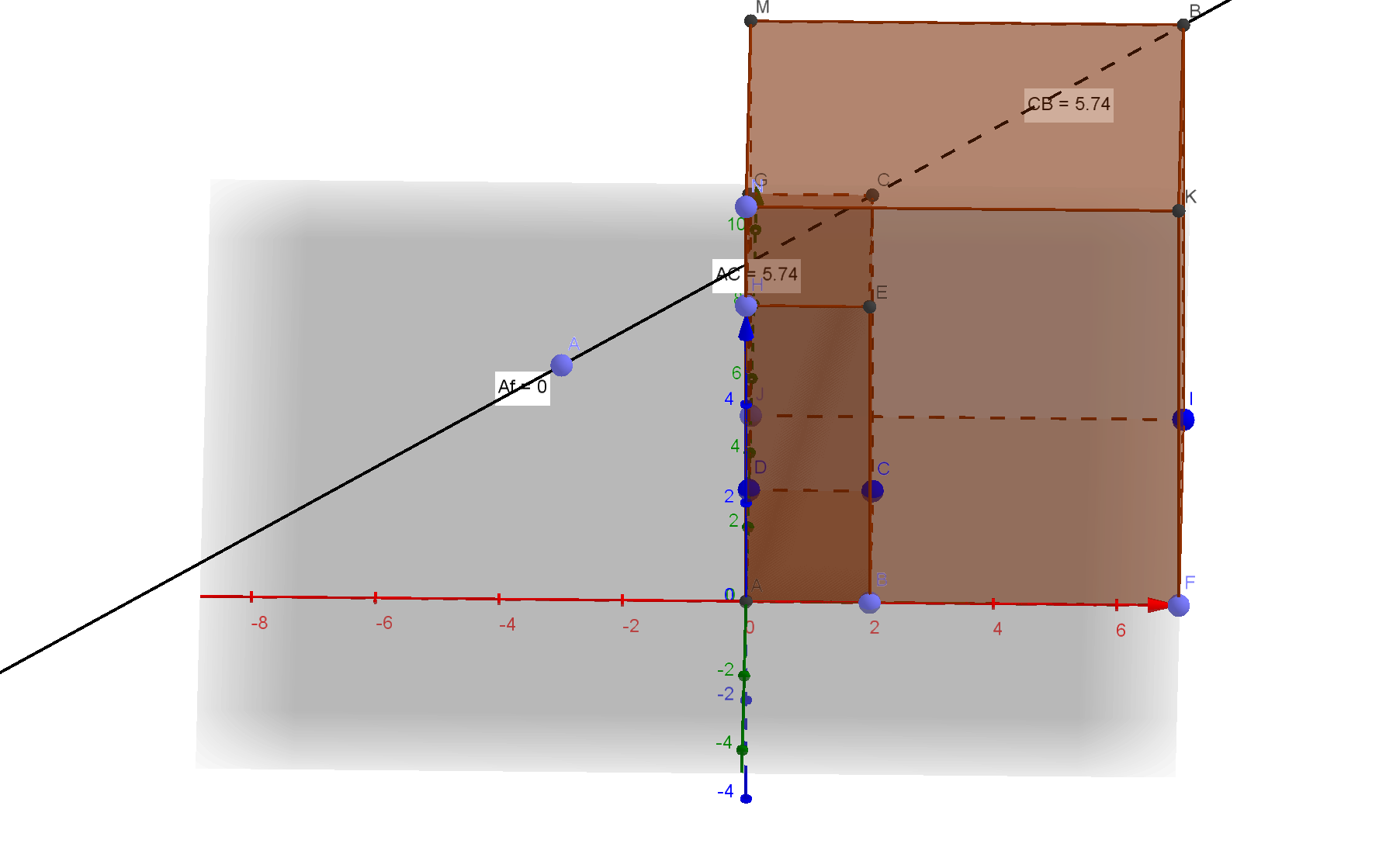
Из протокола видно А(-3,1,4)

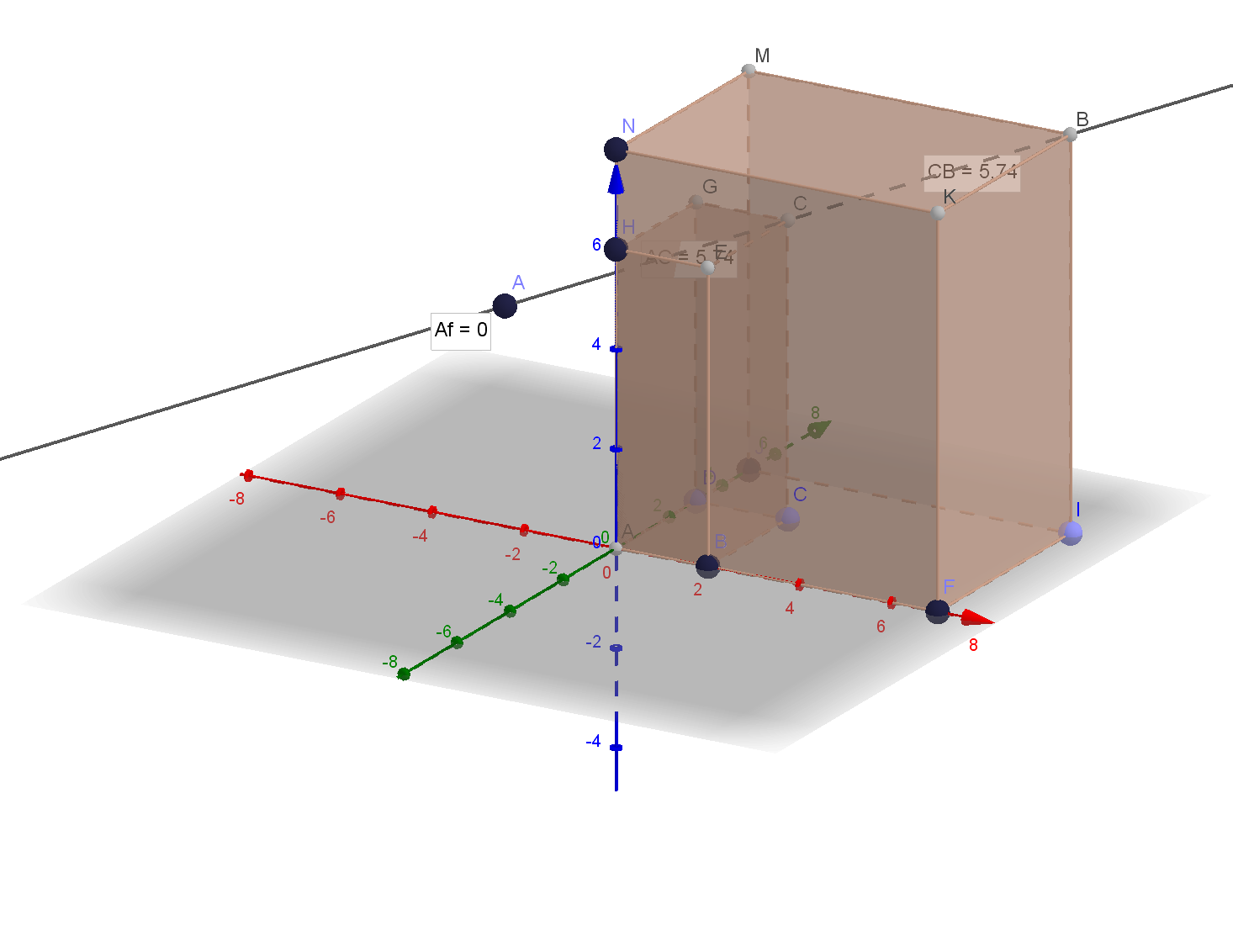
Точка С (2;3;6) является серединой отрезка АВ. Определить координаты точки А, если В(7;5;8).

Решение:

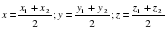
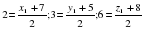
х₁=4-7=-3; у₁=6-5=1; z₁=12-8=4

Ответ: А(-3;1;4)

IV. Закрепление нового материала:

1)Найдите координаты ортогональных проекций точек A(1, 3, 4) и B(5, -6, 2) на: а) плоскость Oxy;

б) плоскость Oyz;

в) ось Ox;

г) ось Oz.

(Ответ: а) (1, 3, 0), (5, -6, 0); б) (0, 3, 4), (0, -6, 2); в) (1, 0, 0), (5, 0, 0); г) (0, 0, 4), (0, 0, 2). )

2 ) На каком расстоянии находится точка A(1, -2, 3) от координатной плоскости: а) Oxy;

б) Oxz;

в) Oyz?

(Ответ: а) 3; б) 2; в) 1)

3 )Найдите координаты середины отрезка: а) AB, если A(1, 2, 3) и B(-1, 0, 1); б) CD, если C(3, 3, 0) и D(3, -1, 2).

(Ответ: а) (1, 1, 2); б) (3, 1, 1).)

Задание на дом §21, 22

Литература:

Ж. Кайдасов, В. Гусев, А Кагазбаева Геометрия 10, 11 классы. Дидактический материал по геометрии для 10, 11 классов.
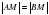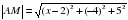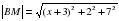