Презентация для 11 класса по теме: "Применение свойств функций в задачах с параметрами"

Применение свойств функций в задачах с параметрами.

Работа учителя математики

лицея №86

Даниловой С. Д.

Применение свойств ограниченности при решении уравнений с параметрами

Метод Мажорант (метод оценки)

Основная идея метода мажорант состоит в следующем:

Пусть мы имеем уравнение и существует такое число  М , что для любого  х  из области определения

Имеем  

Тогда уравнение равносильно системе

Пример 1.   Найти все значения параметра а при каждом из которых уравнение имеет единственное решение

Решение. Оценим обе части уравнения.

Наибольшее значение тригонометрической функции равно 2.

Наименьшее значение квадратичной функции равно ,при уравнение имеет единственное решение

Ответ :

Пример 2.   Найти все значения параметра а при каждом из которых неравенство имеет решение

Решение. Оценим обе части неравенства.

Преобразуем правую часть, выделив полный квадрат

Наименьшее значение квадратичной функции равно 4 и достигается при

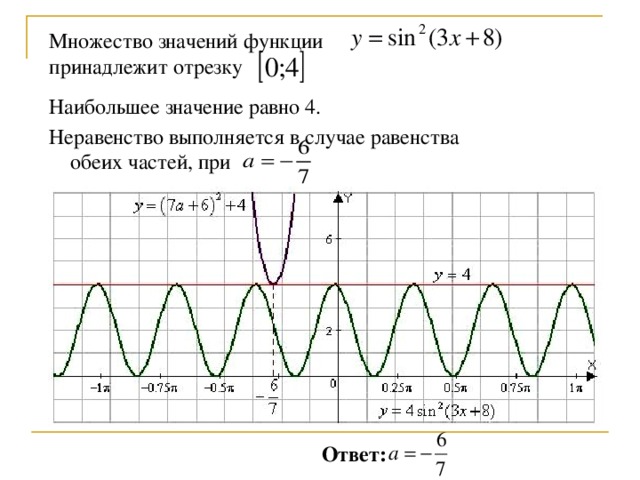
Множество значений функции принадлежит отрезку

Наибольшее значение равно 4.

Неравенство выполняется в случае равенства

обеих частей, при

Ответ:

Пример 3. Найти все значения параметра а при которых уравнение имеет решение

Решение . Оценим обе части уравнения

Найдем множество значений левой части исходного

уравнения.

Оценим множество значений функции

Оценим множество значений функции

Наименьшее значение функции равно 5.

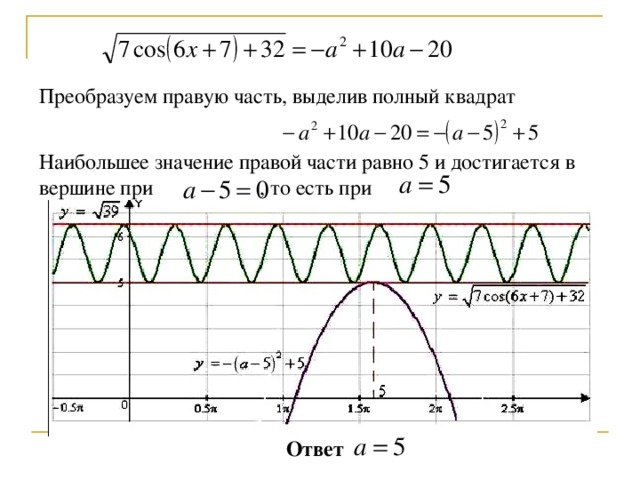
Преобразуем правую часть, выделив полный квадрат

Наибольшее значение правой части равно 5 и достигается в вершине при , то есть при

Ответ

Пример 4 . При каких значениях параметра а из интервала имеет решение уравнение

Решение. Оценим обе части уравнения.

Левая часть уравнения неотрицательна, а правая неположительна, то уравнение

равносильно системе

Решая систему находим

Пример 4 . При каких значениях параметра а из

интервала имеет решение уравнение

Выразим значение а из полученной системы

Учитывая теперь условие задачи, приходим к рассмотрению неравенства

Решая неравенство получаем, что

Ответ:

Применение монотонности при решении уравнений с параметрами

1) Если функции возрастают (убывают) на множестве М , то функция также возрастает (убывает) на множестве М.

2 ) Если функции возрастают (убывают) на множестве М , причем при всех допустимых х , то функция также возрастает (убывает) на множестве М.

3) Если функция монотонная, то уравнение

имеет не более одного корня; другими словами монотонная функция принимает каждое свое значение только один раз.

Пример 1 Решить уравнение

Решение. Функция возрастающая.

Функция постоянна.

Данное уравнение имеет не более одного корня.

Подбором находим - корень

Ответ:

Пример 2 Решить систему у равнений

Решение. Вычтем из первого уравнения второе. Получим

Рассмотрим функцию . Она

возрастающая.

Имеем . Следовательно .

Отсюда

Это уравнение равносильно системе

Решим систему

Очевидно

Ответ: Если , то , если

то решений нет.

Пример 3 Определить число корней уравнения

Решение. Перепишем данное уравнение в виде

Функция возрастает на

Тогда

Исходное уравнение имеет не более одного корня. При

он единственный.

Ответ: Если , то уравнение имеет один корень, если

, то корней нет

Информационные ресурсы

• Амелькин В. В.,Рабцевич В. Л.

Задачи с параметрами: Справ. Пособие по математике.-2-е изд.-Мн.:ООО «Асар», 2002.-464 с.

• П. И. Горнштейн, В. Б. Полонский, М. С. Якир

Задачи с параметрами. 3 издание, дополненное и переработанное.-М.:Илекса, Харьков: Гимназия, 1998,-336с.